MRD:rwz15

H₂ and H system

Question 1

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

Both the minimum of a potential energy surface and the transition structure will have the gradient equal to 0. For the point to be a minimum the second differential will satisfy:

f_xx >0 and f_yy >0

The transition structure will correspond to a saddle point which obeys:

f_xx f_yy - f_xy² <0

The minima is a point on the plot in which any movement from that point will cause an increase in energy. The transition state is a point in which any movement in one direction causes a decrease in energy while movement in the orthogonal direction will cause an increase in energy. This is the case for a two dimensional system. For an nth dimensional system, the first order saddle point will have 1 maxima and N-1 minima where N corresponds to the number of internal coordinates.

Question 2

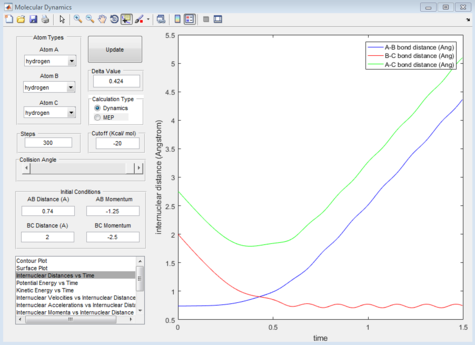
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

Figure 1:Internuclear distance vs time for H + H₂ transition state

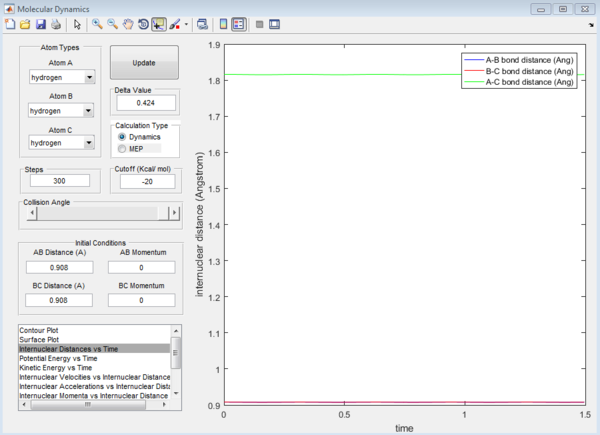
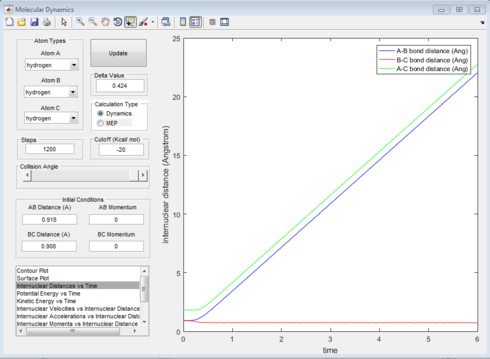
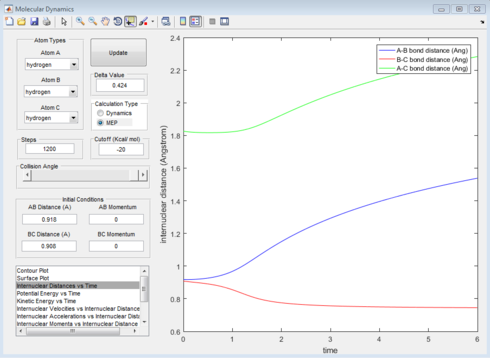
The internuclear distance of the hydrogen atoms at the transition state is 0.908Å. The transition state for this system is the minimal distance between the terminal hydrogens and the central hydrogen in which a slight deviation will induce a bond to be formed and a bond to be broken. As shown in figure 1, this is when the internuclear distance for H_a -H_b and H_b -H_c remains the same over time.

Question 3

Comment on how the mep and the trajectory you just calculated differ.

The dynamic calculation trajectory shows the formation of H₂ (in red) and the ejection of an hydrogen atom (in blue). The MEP calculation shows the same result but at a much slower rate, this is due to the fact that MEP resets the velocity to zero after each time step thus removing the momentum gained by the system over time.The MEP calculation also doesn't show the vibration of the Hydrogen molecule after formation since resetting the velocity to zero removes the kinetic energy for bond vibration at each step.

Figure 2:Internuclear distance vs time for H + H2 dynamic calculation

Figure 3:Internuclear distance vs time for H + H2 MEP calculation

Question 4

Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

Reaction trajectories with varying momenta

p1	p2	outcome	trajectory	comment
-1.25	-2.5	reactive	Figure 4:Reaction 1	This reaction shows that the incoming hydrogen atom has enough momentum and hence energy to displace a hydrogen of the molecule.
-1.5	-2.0	unreactive	Figure 5:Reaction 2	This reaction shows that the incoming hydrogen doesn't have enough energy to overcome the activation energy for a successful reaction.
-1.5	-2.5	reactive	Figure 6:Reaction 3	Upon increasing the momentum of the incoming hydrogen compared to reaction 2, the reaction is now feasible since enough energy is generated upon collision for a successful reaction.
-2.5	-5.0	unreactive	Figure 7:Reaction 4	Although enough momentum and energy was generated upon collision for a reaction, the leaving hydrogen has enough momentum and attraction to the central hydrogen to reform the bond kicking out the incoming hydrogen. This phenomena is known as barrier recrossing.
-2.5	-5.2	reactive	Figure 8:Reaction 5	Increasing the momentum slightly compared to reaction 4 for the incoming hydrogen gives a successful reaction. Although barrier recrossing occurs, the incoming hydrogen still has enough energy to eject the hydrogen to form a new H-H bond.

Question 5

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory (TST) states that:

1. Once a supermolecule crosses the critical dividing surface (transition state) then the products will be formed.

2. During the reaction, the Boltzmann distribution is maintained.

3. The Boltzmann distribution of the supermolecule passing through the transition state corresponds to the temperature of the system.

Compared to experimental values, TST predicts that reaction rates are much faster since upon crossing the transition state, products are formed. However this is not the case since the theory breaks down as the Boltzmann is not maintained. This can be seen with reaction 4 in figure 7 as a process called barrier recrossing occurs which can lead to the products not forming even after crossing the transition state. Also in figure 8, reaction 5 shows that although the supermolecule crosses the transition state, the products are not immediately formed due to barrier recrossing followed by the successful re-attack of the initial incoming hydrogen thus increasing reaction rate. (TST has some more assumptions in addtion to this Lt912 (talk) 08:17, 9 June 2017 (BST))

The H₂ and F system and the HF and H system

Question 6

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Figure 9:Surface plot of the energetics of HF formation

Figure 10:Surface plot of the energetics of HH formation

Figure 11:Surface plot of the energetics of the transition state

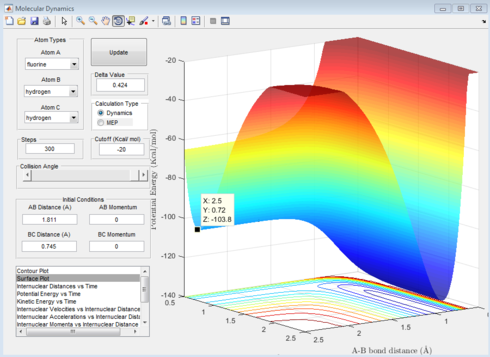
The F + H₂ reaction is exothermic as the energy of -560.24kJmol^-1 is lower than the transition state of -432.20kJmol^-1. The H + HF reaction is endothermic as its energy of -434.30kJmol^-1 is higher than the energy at the transition state.

The bond energy for HF is -568.19kJmol^-1 and the bond energy for HH is -435.97kJmol^-1. The formation of HF gives off 132.22kJmol^-1 of energy so is exothermic while it requires an extra 132.22kJmol^-1 of energy to break the HF bond to form the hydrogen molecule so it is endothermic.

The data from literature and our matlab calculations vary because our calculations come from empirically derived parameters. To reduce the difference from literature we can derive it using quantum mechanics.

Question 7

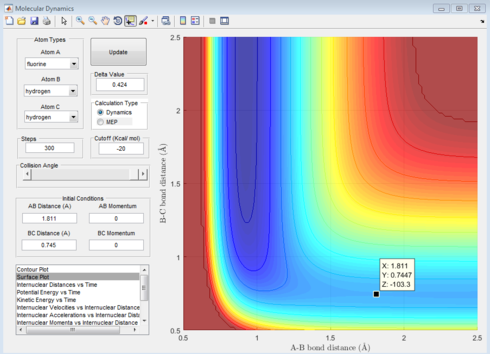
Locate the approximate position of the transition state.

Figure 12:Internuclear distance vs time for H-H-F transition state

The position of the transition state is when the F-H distance is 1.811Å and the H-H distance is 0.745Å. As shown in figure 12 this occurs when the internuclear distance does not change over time.

Question 8

Report the activation energy for both reactions.

Figure 13:Potential energy vs time for HF formation

Figure 14:Potential energy vs time for HH formation

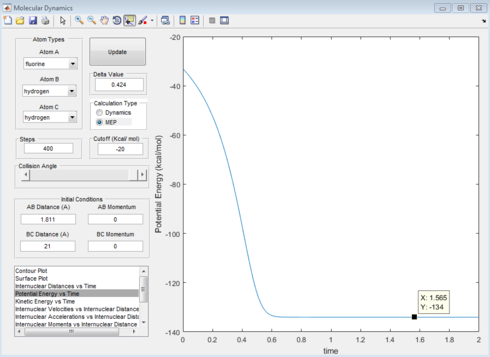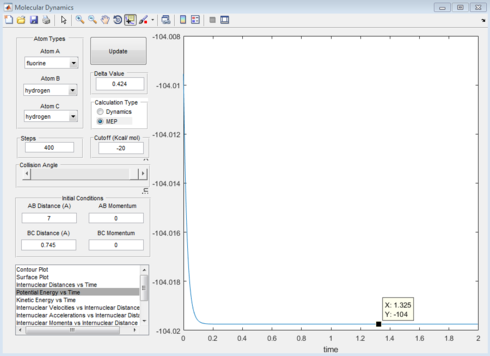The activation energy for HF formation is 2.10kJmol^-1 and for HH formation is 128.04kJmol^-1.

Question 9

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Figure 15:Internuclear momentum vs time for F + H₂

At time=0, the F has a high amount of translational energy and the H₂ molecule has vibrational energy. As F gets closer to the hydrogen molecule, translational energy is converted into vibrational energy, at the transition state momentarily, vibrational energy is at its maximum and translational energy is at its minimum. Upon forming the bond, H-F now has a new vibrational energy and the excess energy is turned into translational energy for the leaving hydrogen. We can confirm the energy released in this process by calorimetry.

(what about potential energy? Lt912 (talk) 08:13, 9 June 2017 (BST))

Question 10

scuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

According to Polanyi's rules, vibrational energy promotes a late transition state, this is due to the fact that during bond formation it is the vibrations of the new bond which dominates the system. For an early transition state, translational energy dominates since it is the incoming velocity of the atom which influences the chance of bond formation.

For a late transition state, high vibrational energy is favourable for a reaction because it would increase the chances for the molecule to move from the reeactant channel to the product channel where the late transition state lies while purely translational energy would cause the incoming atom to move up the wall without reaching the transition state. For an early transition state translational energy is needed to reach beyond the transition state.

We would expect that a higher translational energy from the incoming atom to be more likely to react due to higher chance of collision with enough energy to displace an atom of the molecule. Higher vibrational energy of the molecule would mean that the bond is weaker since at maximum displacement the atoms of the molecules are far away from each so more likely to be displaced. Although this is what we expect, there are other factors which influence whether a reaction will take place such as orbital overlap during collision and other symmetry factors.