MRD:rkf75

H + H₂

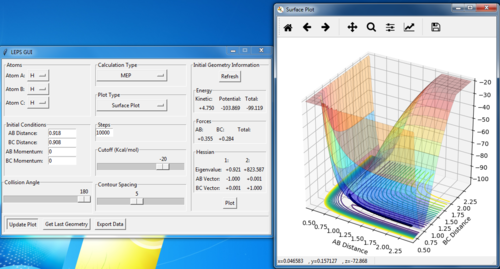
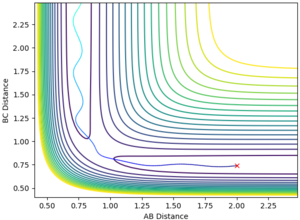
AB=	2.3
BC=	0.74
p(AB)=	-2.7
p(BC)=	0

At a transition structure and at a minimum both components of the gradient are 0. The two can be differentiated by the curvature as minimums are stable physical structures that are minimums on the potential energy surface where are transition states are saddle points on the potential energy surface. The second derivative can be used to tell the difference between a saddle point by using the second derivative discriminant test:

δ = f_xxf_yy − f²_xy ≥ 0'

for a saddle point δ<0

for a minimum δ>0

Good, so my questions are: 1. Why for a saddle point, δ<0 and for a minimum δ>0? 2. What does it actually mean on your energy surface plot that TS is a saddle point? Why is that? --Sw2711 (talk) 12:12, 21 May 2018 (BST)

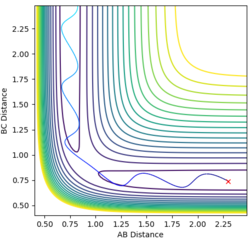
Locating the transition state

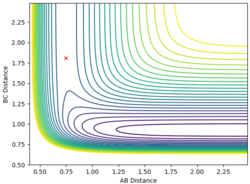
AB=BC=1	p(AB)=p(BC)=0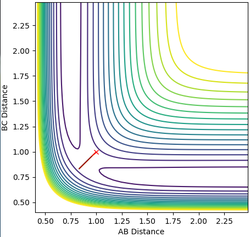
AB=BC=0.75	p(AB)=p(BC)=0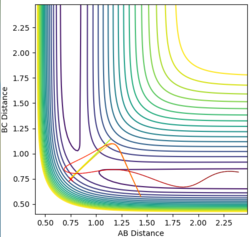
AB=BC=0.908	p(AB)=p(BC)=0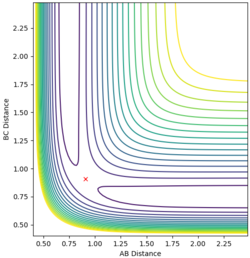

The best transition state estimate:

This is the best estimate of the transition state is AB=BC=0.908 to 3dp as it gives the straightest distance vs time graph therefore there is the littlest oscillation

Again, I need a bit more explanation about why you tested this way. --Sw2711 (talk) 12:12, 21 May 2018 (BST)

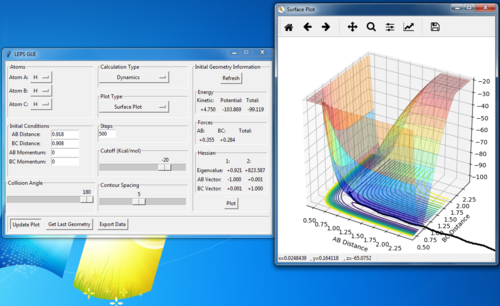
The reaction path

MEP vs dynamic calculations

The AB distance increases much faster in far less steps. Also the trajectory shows some oscillation in the dynamic calculation but not in the MEP calculation.

You probably need a bit more explanation about why no oscillation observed in MEP--Sw2711 (talk) 12:12, 21 May 2018 (BST)

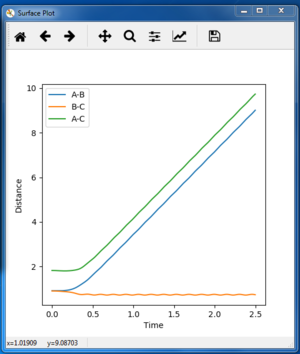
The dynamic trajectory

Final AB = 10 tending to infinity

Final BC = 0.74

Average p(AB) = 2.5

Average p(BC) = 1.25

If instead r1 = r_ts and r2 = r_ts+0.01 then BC would AB and BC values would swap therefore BC would tend to infinity and AB would oscillate around 0.74.

If the initial conditions are set to the final distances above and the negative momentums then the system resorts back to the transition state as seen by the surface plot below.

Reactive and nonreactive trajectories

caption
AB	BC	P(AB)	P(BC)	Total energy	Reactive?	Description
2	0.74	-2.5	-1.25	-100	yes	As atom A approaches molecule BC the transition state is reached and the reaction proceeds to give molecule AB and atom C
2	0.74	-2.0	-1.5	-100	no	as molecule atom C and molecule AB move towards each other the transition state is not quite reached before the direction changes
2	0.74	-2.5	-1.5	-100	yes	As atom A approaches molecule BC the transition state is reached and the reaction proceeds to give molecule AB and atom C
2	0.74	-5.0	-2.5	-85	no	As the system approaches the transition state and the boundary for the reaction is crossed there the energy is enough that the boundary can be recrossed and the reaction does not proceed
2	0.74	-5.2	-2.5	-84	yes	As the system approaches the transition state and the boundary for the reaction is crossed there the energy is enough that the boundary can be recrossed and then recrossed again meaning the reaction proceeds

The transition state theory assumes that systems that reach the transition state proceed to react however this is always true for cases with higher total energy where the boundary can be recrossed and the reaction will not proceed. For cases where the energy is high enough to recross the barrier transition state theory will predict a higher rate as when boundary recrossing occurs and the reaction does not proceed transition state theory predicts that it will proceed.

This part is good.--Sw2711 (talk) 12:12, 21 May 2018 (BST)

F-H-H system

PES inspection

F + H ₂ is exothermic

H + HF is endothermic

This shows that the H-F bond is stronger than the H-H bond.

I need some explanation or evidence on why or how you know one is exothermic and the other is endothermic. How does it relate to PES?--Sw2711 (talk) 12:13, 21 May 2018 (BST)

Transition state

Atom C = F

Atom A + B = H

AB=	0.747
BC=	1.809
p(AB)=	0
p(BC)=	0

I need some evidence and explanation how you got those numbers. --Sw2711 (talk) 12:14, 21 May 2018 (BST)

activation energy

activation energy HF + H= 30 kJ/mol

activation energy H₂ + F = 0.2 kJ/mol

I need some evidence and explanation.--Sw2711 (talk) 12:14, 21 May 2018 (BST)

H₂+F

Reactive conditions:

AB=	0.747
BC=	3
p(AB)=	-0.5
p(BC)=	-2.5

Energy released in the reaction is converted into vibrational energy of the H-F bond as shown by the momentum time graph below. It can be seen from this graph that there is significantly more momentum in the B-C bond at later times than there is in the A-B bond at earlier times. This can be confirmed experimentally by comparing the change in temperature to that which would be expected from the enthalpy of reaction.

Good--Sw2711 (talk) 12:15, 21 May 2018 (BST)

caption
AB	BC	P(AB)	P(BC)
0.74	2.2	-2.9	-0.5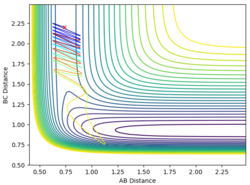
0.74	2.2	-0.7	-0.5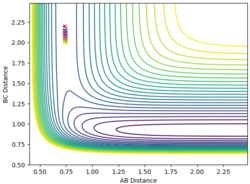
0.74	2.2	-0.5	-0.5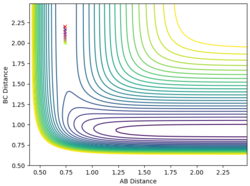
0.74	2.2	-0.3	-0.5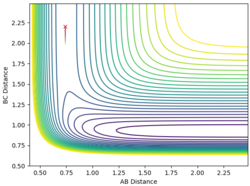
0.74	2.2	0	-0.5
0.74	2.2	1.2	-0.5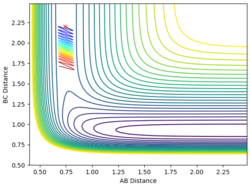
0.74	2.2	2.9	-0.5

When the momentum of AB is close to the limits -3 and 3 the reaction has enough energy to cross the barrier to react but it recrosses back again. In between this range there is not enough energy in the system for the reaction to be successful.

AB=	0.74
BC=	2
p(AB)=	0.1
p(BC)=	-0.8

Under these conditions the reaction is successful as seen by the plot below.

HF+H

caption
AB	BC	P(AB)	P(BC)	Reactive
2	0.9	-4	-0.1	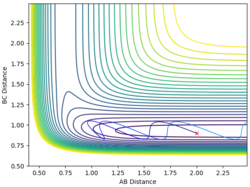No
2	0.9	-3	-0.3	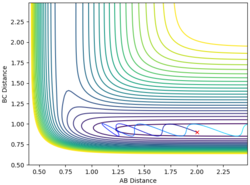No
2	0.9	-2	-0.7	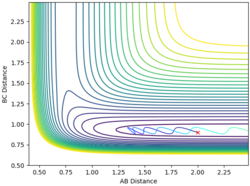No
2	0.9	-1.5	-10	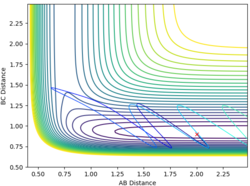No
2	0.9	-1.2	-9.6	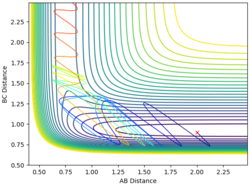Yes
2	0.9	-1.1	-9.2	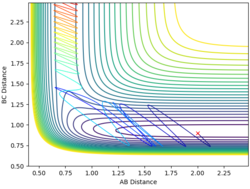Yes

From the examples above reactions, for a reaction to be successful there must be both vibrational and translational energy. When the transition state is symmetrical there must be higher translational energy for the reaction to be successful. When the transition state is closer to the reactants there must be higher initial translational energy and when the transition state is closer to the products there must be significantly higher initial vibrational energy.

For both reaction sets, good experiments and observation. But in terms of your explanation, I think it would be useful if you could tell me which reaction has a late TS (closer to product) and which one is early TS (closer to reactants). Why do you change both of the momenta? What does it mean? You need to try to explain things step by step in a consistent and logical way. Sometimes, simply sticking some figures does not really help. --Sw2711 (talk) 12:26, 21 May 2018 (BST)

H + H2