MRD:ri3717 summer 2019
Exercise 1: H+H2 system
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is mathematically defined as:
where q1 and q2 are the reactant molecules, V is the potential energy.
The transition state can be identified by starting trajectories near the transition state and if they move towards reactants or products (even with no initial momentum) then it is the transition state. It can be distinguished from a local minimum by calculating the second derivative, which gives a negative value for a local minimum but a positive value for a local maximum (i.e. the transition state).
Are you sure about your statement? TS is the maximum point on the minimum energy pathway. A saddle point, in this case, the TS point, is a point where in a 3-dimensional space, it is both a maximum and a minimum at the same time, depending on which plane you are looking at. That differentiates from a local minimum or a maximum, because whichever plane you are looking at, it's always a minimum or a maximum. Please check the figure that I attached.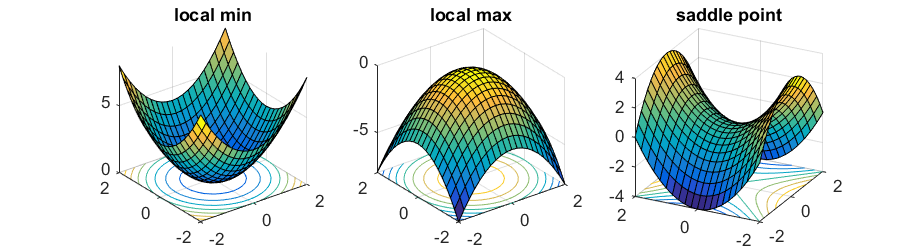 
Sw2711 (talk) 12:04, 30 May 2019 (BST)
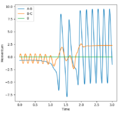
Report your best estimate of the transition state position (rts) for trajectories from r1 = r2 and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
The transition state position is the position at which the distance between A-B (r1) and B-C (r2) is equal, as it is symmetrical for this particular reaction. However, for trajectories from r1 = r2, the H atoms perform oscillation, so the transition state position needs to be estimated by testing different r values. The transition state position (rts) found with r1 = r2 is 0.908 Å. At this distance, there is almost no oscillation as shown in the Internuclear Distance vs Time plot below:
This shows that at this value of r, the H atoms do not move with no initial momentum, which is characteristic of a transition state. This part is good. Sw2711 (talk) 12:05, 30 May 2019 (BST)
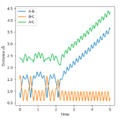
Comment on how the MEP and the trajectory you just calculated differ.
For trajectories with r values below:
r1 = rts + 0.01 = 0.909
r2 = rts = 0.908,
the MEP and Dynamics trajectories are compared.
-
Initial conditions of the three H atoms. Momenta= 0
Dynamics
Animation- B moves towards the C and A moves away from the rest. H atoms B and C continue to move to the right as they oscillate.
Internuclear distances- stays constant for a short time and A-B and A-C distances increase as they move away from each other, while B-C distance decreases and fluctuates as the molecule performs an oscillation. At large t, the final value of B-C distance is approx. 0.75.
Momenta- the momentum of A-B (p1(t)) increases with time; rapid increase at first then continues to slowly increase to a limit. The momentum of B-C (p2(t)) decreases first, then increases with fluctuation. At large t, p1(t) reaches a limit at 2.5 and p2(t) oscillates between 1.0-1.5, giving an average of 1.25.
The angle θ stays constant at 0.
MEP
Animation- a smooth movement of the H atom in the centre towards the H atom on the right as the H atom on the left accelerates towards left.
Internuclear distances- stays constant for a very short time and A-B and A-C distances increase as they move away from each other, while B-C distance decreases without fluctuation. At large t, the final value of B-C distance is approx. 0.75.
Momenta- no change, constant at 0.
When the r1 and r2 values are swapped, H atom A and C swap roles- A and B forms a molecule, C moves away to the right.
This part, it is very descriptive. Very good observation. But you haven't really shown much understanding, like what do you understand why these differences occur by using two different algorithms?
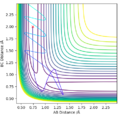
Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table.
This part, in general is good. But you need to improve on your descriptions. Just wondering, did you write all that by looking at the animations? It will be better if you could talk more, in terms of the energy, transition state, e.g. system #2 doesn't acquire enough activation energy to reach the transition point, therefore, the reaction doesn't occur. --- something like that, I'm sure you can do a better job than me. Sw2711 (talk) 12:16, 30 May 2019 (BST)
| # | p1 (kg.m/s) | p2 (kg.m/s) | Etot (kcal/mol) | Reactive? | Description of the dynamics |
|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -99.0 | yes | As molecule A-B approaches C, B is pulled away from A, forming molecule B-C. A moves away to the left, B-C moves to the right with oscillation. |
| 2 | -1.5 | -2.0 | -100.5 | no | Molecule A-B and atom C slowly approaches each other, and when they get to a certain distance, they repel and moves away from each other. |
| 3 | -1.5 | -2.5 | -99.0 | yes | As molecule A-B slowly approaches C, B is pulled away from A, forming molecule B-C. A moves away to the left, B-C moves to the right with oscillation. |
| 4 | -2.5 | -5.0 | -85.0 | no | Molecule A-B approaches C and B is pulled away from A. B-C oscillates but gets too close and repel each other, pushing B back to A, forming molecule A-B. |
| 5 | -2.5 | -5.2 | -83.4 | yes | Same as the one above happens, but molecule A-B oscillates again, gets too close and repel each other, pushing B back to C, finally forming molecule B-C. |
Although there is no simple trend in the reactivity and the initial conditions, It is evident that small changes to the initial conditions (momentum and hence the total energy) can affect the reactivity. For example based on the last two sets of initial conditions (conditions 4 and 5), we can see that increasing the magnitude of p2 by 0.2 kg.m/s increases the total energy by 1.6 kcal/mol, and enables the reaction between molecule A-B and atom C, forming atom A and molecule B-C.
-
Initial conditions #1
-
Initial conditions #2
-
Initial conditions #3
-
Initial conditions #4
-
Initial conditions #5
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The main assumptions of Transition State Theory are[1]:
- the reactants are in thermal equilibrium and therefore the energy of the particles can be calculated by the Boltzmann equation
- the reactants and the transition state are in equilibrium
- reactants that has reached the transition state with some velocity towards the product will not form back the reactants again.
The transition state theory predictions for reaction rate values ignores the fact that the reaction may not proceed even with energy higher than the activation energy. For example, with initial conditions #4 discussed previously, the reactants approach each other with enough energy and reacts, but the product forms back the reactant species, so there is no reaction overall. This means that the transition state theory predicts reaction rate to be faster than the experimental rate.
This part is good. Please be aware that terms like 'Boltzmann'; 'equilibrium' are not very applicable in our case, because we only have three atoms in the system. Sw2711 (talk) 12:12, 30 May 2019 (BST)
Exercise 2-1: F-H-H system
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 is exothermic, H + HF is endothermic.
H-F bond is stronger (bond strength~ 565 kJ/mol[2]) than H-H bond (bond strength~ 432 kJ/mol[2]) because although both are covalent bonds and have good orbital overlap due to the same or very similar sized orbitals. H-F is highly polar while H-H bond is purely covalent. This means that the formation of H-F bond is favourable in the reaction F + H2 even with the need to break the H-H bond and thus exothermic, while for the reverse reaction of H + HF, the breaking of H-F to make H-H bond is overall not stabilising and thus the reaction is endothermic.
Did you get the conclusion by checking the values, your prior knowledge or the energy surfaces plot? Did you notice in the energy surface plot, the channel representing H-F + H system is lower in energy compared to H-H + F system. That's why from H-H + F -> H-F + H is from a higher energy surface to a lower energy surface, releasing energy. That's why it is exothermic. Sw2711 (talk) 12:20, 30 May 2019 (BST)
Locate the approximate position of the transition state.
The transition state for the F-H-H system is not symmetrical, so the distance between F-H (r1) and H-H (r2) is not equal. With the initial conditions r1= 1.814 Å, and r2 = 0.745 Å, the three atoms F, H, H do not move as shown in the internuclear Distances vs Time plot below, which is indicative of a transition state.
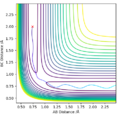
The surface plot also shows the position of the transition state at r1= 1.814 Å, and r2 = 0.745 Å as the black spot on the graph is stationary.
Focusing on the reaction of F + H2, which is exothermic, the transition state is a "early" transition state. based on the Hammond's postulate, the structure of the transition state is energetically closer and similar in structure to the reactants. This agrees with the internuclear distances (r1 and r2) obtained for the transition state since the distance between the two H atoms is much shorter than the distance between F and H.
This part is goodSw2711 (talk) 12:21, 30 May 2019 (BST)
Report the activation energy for both reactions.
Now choosing a point close to the transition state, the set of initial conditions is r1= 1.804 Å, and r2 = 0.745 Å. This yielded the following Energy vs Time graph:
The decrease in potential energy (hence the total energy) was determined from the graph as 29.9 kcal/mol. This is indicative of the energy difference between the transition state and the (F-H + H) state. Therefore this is the activation energy for the endothermic reaction between HF + H. For the activation energy of the reaction F + H2, another set of initial conditions is tested: r1= 1.824 Å, and r2 = 0.745 Å. This yielded the following Energy vs Time graph:
The energy change is very small even at a very large value of t (t= 3000). The activation energy of the reaction F + H2 is estimated to be 0.2 kcal/mol.
This part is also very good. Sw2711 (talk) 12:22, 30 May 2019 (BST)
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
Initial conditions: r1= 2.0, r2 = 0.7, p1= -0.7, p2 = 0
Observations from Animation: The H2 molecule moves towards F and one of the H atoms gets pulled towards F. Then it is bounced back to H, vibrates, and forms back H-F and H in the end.
As shown in the Momenta vs Time graph below, the overall momentum has increased after reaction. The reaction energy has been transferred to the products in the form of kinetic energy (vibration).
-
Momenta vs Time
This could be confirmed experimentally by monitoring the change in temperature as the energy could be released to or absorbed from the environment as heat. As F+H2 is an exothermic reaction, the temperature is expected to increase on reaction.
Good, but how does the change in moment from reactants to products prove the conservation of energy? What's the method called by measuring the change in temperature? Sw2711 (talk) 12:31, 30 May 2019 (BST)
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.
For initial conditions rFH = 2.10, rHH = 0.74 and pFH = -0.5, different values of pHH between -3 and 3 were tested and results are shown below.
| # | pHH (kg.m/s) | Reaction? | Observation |
|---|---|---|---|
| 1 | -3.0 | no | H-H molecule vibrates for a while, then one of the H atoms gets closer to F, forming H-F for a very short while. Then the H atom gets pushed back and forms back H-H. |
| 2 | -2.9 | yes | H2 molecule moves closer to the F atom as it vibrates, and eventually one of the H atoms forms a bond with F. The remaining H gets repelled and moves away, resulting in H-F and H. |
| 3 | -2.0 | yes | same as above but reaction happens more slowly. |
| 4 | -1.0 | yes | same as above but reaction happens more slowly. |
| 5 | 0 | no | H2 molecule vibrates and moves towards the F atom until it gets repelled by F and moves away. |
| 6 | 1.0 | yes | H2 molecule moves closer to the F atom as it vibrates, and eventually one of the H atoms forms a bond with F. The remaining H gets repelled and moves away, resulting in H-F and H. |
| 7 | 2.0 | yes | Same as above but reaction happens more quickly. |
| 8 | 2.9 | yes | Same as above but reaction happens more quickly. |
| 9 | 3.0 | no | H-H molecule vibrates for a while, then one of the H atoms gets closer to F, forming H-F for a very short while. Then the H atom gets pushed back and forms back H-H. |
For the same initial position, increase slightly the momentum pFH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.1. What do you observe now?
Initial conditions: rFH = 2.10, rHH = 0.74 and pFH = -0.8, pHH = 0.1
-
Starting positions of F and H-H
Observation: A vibrating hydrogen molecule slowly approaches an F atom. One of the H atoms (HA) gets pulled towards the F atom, producing F-HA and HB, but HA gets repelled and moves back towards HB, producing back the reactant, F and H-H. Then the HA atom gets repelled by HB and bonds to F again, ending with F-H and H.
-
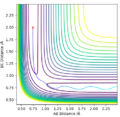
Contour plot of the reaction
Very good effort for recording all these different trials. As I said above, you need to improve the way you describe your observations Sw2711 (talk) 12:33, 30 May 2019 (BST)
Exercise 2-2: H + HF System
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Initial conditions #1: rFH = 0.92, rHH = 1.5 and pFH = -0.1, pHH = -2.5
I have set the initial conditions at the bottom of the entry channel (H + HF reactant conditions) with very low pFH, and obtained a reactive trajectory by decreasing pHH and increasing pFH, which is:
Initial conditions #2: rFH = 0.92, rHH = 1.5 and pFH = -10.0, pHH = -1.0
-
Initial conditions (F-H, H)
-
After reaction (F, H-H)
-
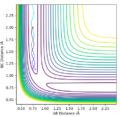
Contour plot for the reaction between F-H and H, producing F and H-H
-
Change in internuclear distances during and after reaction
For a given amount of total energy, the distribution of energy between different modes can affect the efficiency of the reaction. For example, even with enough total energy to overcome the energy barrier for the reaction to occur, if there is not enough translational energy, the reactants will not come close enough to react.
The Polanyi's empirical rules state that in simple terms, translational energy is more effective in activating the reactants for exothermic reactions, while vibrational energy is more effective for endothermic reactions[3]. The relationship can also be shown as below:
Ea = mΔH + constant
where Ea= activation energy, m= indicative of the position of transition state on the reaction coordinate[4]. The position of the transition state is important because it determines which of the two modes, the translational energy or the vibrational energy has a larger influence on the efficiency of the reaction.
Looking at initial conditions #1 ( rFH = 0.92, rHH = 1.5 and pFH = -0.1, pHH = -2.5 ) in which the reaction did not take place, we can say based on the Polanyi's rules that since this is an endothermic reaction (H + H-F --> H-H + F), vibrational energy has a more significant impact on the reaction efficiency. the momentum in F-H bond is set very low at -0.1, and this is why the reaction does not take place in these conditions.
Now looking at initial conditions #2 ( rFH = 0.92, rHH = 1.5 and pFH = -10.0, pHH = -1.0 ), the reaction was successful and we can see why based on the Polanyi's rules. In initial conditions #2, the momentum in F-H bond is now set very high at -10.0, which provided the reactants with enough vibrational energy to react.
This part is very good. Sw2711 (talk) 12:35, 30 May 2019 (BST)
References
- ↑ Bligaard, T., and J.k. Nørskov. “Heterogeneous Catalysis.” Chemical Bonding at Surfaces and Interfaces, 2008, pp. 255–321., doi:10.1016/b978-044452837-7.50005-8.
- ↑ 2.0 2.1 Yoder, Claude. “Wired Chemist.” Common Bond Energies (D) and Bond Length (r), www.wiredchemist.com/chemistry/data/bond_energies_lengths.html.
- ↑ Bowman, Joel M. “Dynamics of the Reaction of Methane with Chlorine Atom on an Accurate Potential Energy Surface.” Science, American Association for the Advancement of Science, 21 Oct. 2011, science.sciencemag.org/content/334/6054/343.
- ↑ Wubbels, Gene G. “The Bell–Evans–Polanyi Principle and the Regioselectivity of Electrophilic Aromatic Substitution Reactions.” Tetrahedron Letters, vol. 56, no. 13, 2015, pp. 1716–1719., doi:10.1016/j.tetlet.2015.02.070.