MRD:pes116
Applying Molecular Reaction Dynamics to Triatomic Systems
Transition States
At the transition state and at a minimum, the gradient is 0 with respect to both r1 and r2. At the transition state, the potential energy surface will have a saddle point. If a structure at this point is displaced slightly from the transition state, the potential gradient becomes negative and the structure will roll towards the products or the reactants. At a minimum, any change in geometry results in an increase in potential energy, as the reactants and products are at the minima and any movement away from these results in the structure becoming more like the unstable transition state.
Jas213 (talk) 13:21, 28 May 2018 (BST) You've mentioned the gradient, what about the second derivative? What does it tell you? The gradient alone is not enough. Some equations wouldn't have hurt, taking into account the dimensionality of the problem.
H + H2 system
Locating the transition state
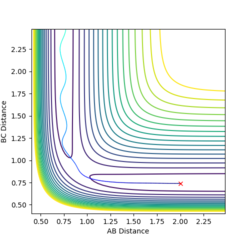
By testing various initial conditions with r1 = r2 and p1 = p2 = 0, it was found that rts = 0.9078. The contour plot when r1 = r2 = rts (Figure 1) shows the structure is held at the potential energy maximum.
At this point, there is no displacement of the atoms as shown by the Internuclear Distance vs. Energy plot (Figure 2).
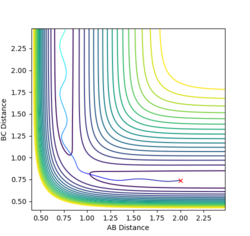
If the atoms are displaced slightly from rts, the structure will roll towards the reactants or products. Figure 3 shows contour plot when r1 is displaced by a small amount, δ. The plot (Figure 3) shows that the products are formed. If an mep calculation is used, the structure still rolls towards the products, but there is no vibration of the structure as it is travelling towards the products. When mep is used for the calculation (Figure 4), the structure takes the lowest energy path, whereas using a Dynamics calculation, there is some vibration as the structure moves towards the products.
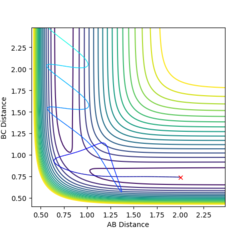
When this calculation is run, the final values of the positions are r1 = 9.00 and r2 = 0.74. The final values of the momentum are p1 = 2.48 and p2 = 1.24. Running the calculation with these values as the initial conditions produces the plot shown in Figure 5.
Jas213 (talk) 13:24, 28 May 2018 (BST) Good comparison between men and dynamics in the previous plots, what are you trying to do now? Why do you start 9 Angstroms far apart? How many steps did you use if you start that far apart? Is this a dynamics plot again?
If r2 is displaced by δ rather than r1, the structure will roll towards the reactants instead, as shown in Figure 6.
Reactive and unreactive trajectories
The table below shows the results of testing varying values of momenta with a reaction where r1 = 0.74 and r2 = 2.0, to see if the reaction proceeds.
| Reaction | p1 | p2 | Energy | Reactivity | Plot | Analysis |
|---|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -99.018 | Reactive |  |
The components have the correct amount of transitional momentum to overcome the activation energy, so travel through the transition state, to the products. |
| 2 | -1.5 | -2.0 | -100.456 | Unreactive |  |
The components don't have the enough momentum to react, as they travel towards the transition state, but can't overcome the energy barrier. They roll back to the reactants. |
| 3 | -1.5 | -2.5 | -98.956 | Reactive |  |
The reactants have more energy than in the first reaction, so can successfully overcome the energy barrier and react. Because of the extra energy, the products have greater vibrational energy. |
| 4 | -2.5 | -5.0 | -84.956 | Unreactive |  |
The reactants have a lot of transitional momentum, so though they collide and a new bond forms between the H atom and a H from the molecule, the atoms in this bond vibrate too vigorously. They come too close together, so coulombic repulsion pushes them apart, and back to the reactants. |
| 5 | -2.5 | -5.2 | -83.416 | Reactive |  |
Though the H atom has even more momentum than in reaction 4, this allows the reactant to be pushed through the transition state, which again involves lots of vibration. After the reaction, the products are left with lots of vibrational energy. |
Jas213 (talk) 13:28, 28 May 2018 (BST) What did you learn from this table? An overall concluding comment would have been expected.
Transition State Theory
Transition state theory assumes that:
- The atoms in the reaction are Boltzmann distributed
- Quantum tunnelling effects are negligible
- Once the system reaches the transition state with a velocity towards the products, it will not convert back to the reactants.[1].
- The reactants are in a quasi-equilibrium with the transition state.[2]
As the Transition state theory doesn't allow for quantum tunnelling, there will be some reactions which the theory forbids, but which will be shown as successful by the programme. Also, the programme shows it is possible for reactants to reach the transition state, but then return to the reactants, as shown by the plot in Figure 9. This would be forbidden by Transition state theory.
Jas213 (talk) 13:27, 28 May 2018 (BST) Good referencing style, good you mentioned quantum tunnelling and pointed out the contradiction between TST and Figure 9. (Next time label Figure 9 as figure 9)
F - H - H system
The reactions between F and H2 and the reaction between H and HF were studied. The first reaction is exothermic, as the HF bond which forms during the reaction is strong, with a bond dissociation energy of 136.25 kcalmol-1, so the formation of it releases a lot of energy. The reaction between H and HF, however, is endothermic as the products which form are less stable than the reactants. The bond dissociation energy of H2 is smaller than that of HF, at 104.206 kcalmol-1.[3]
Jas213 (talk) 13:29, 28 May 2018 (BST) Nice that you give bond energies, you could have additionally taken a photo of the surface plot showing the height of the reactant vs product channel.
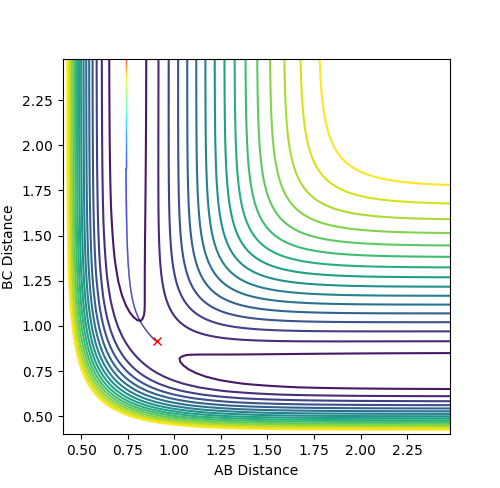
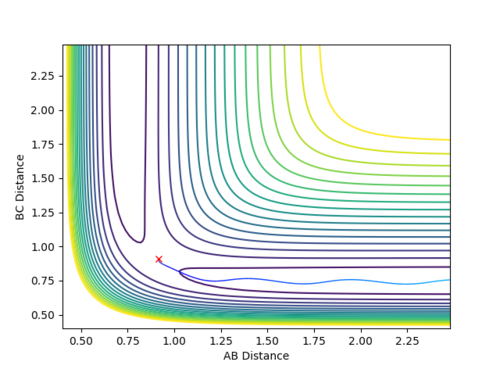
Locating the transition state
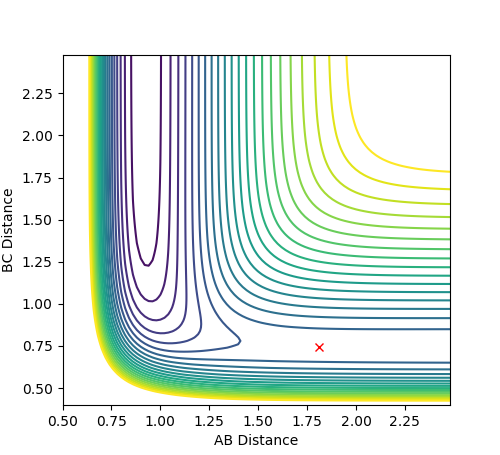
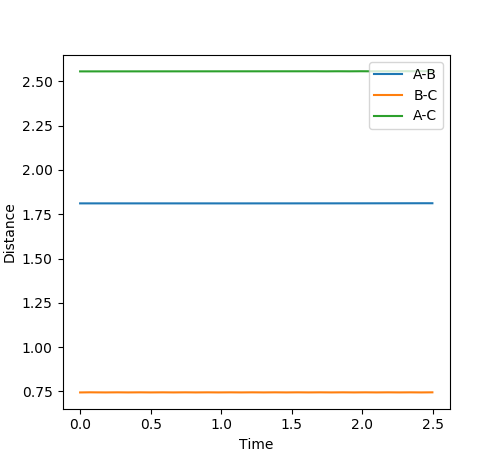
The transition state was located by testing different values of r1 and r2 with both values of momentum set to 0. It was found that the transition state is located at approximately r1 = 0.7447 and r2 = 1.811, as shown in Figure 11. The Internuclear Distance vs. Energy plot (Figure 12) was used to confirm the position of the transition state, as it shows that at this position, there is no movement of the atoms.
Activation Energy
The activation energies for each of the reactions were found by displacing the structure slightly from equilibrium in the direction of the reactants, then the direction of the products, allowing the structure to roll towards the reactants or products (Figure 13 and Figure 14).
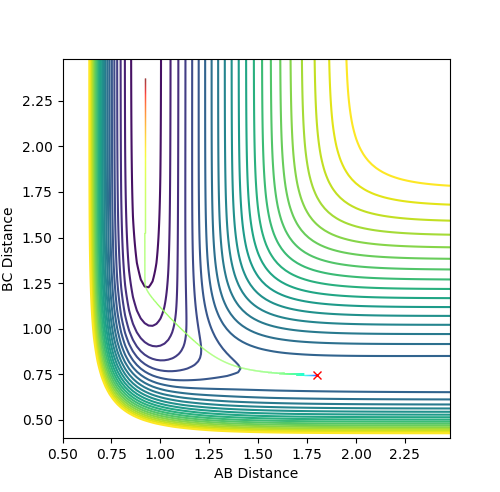
An mep calculation was used and the momenta were set to 0. The Energy vs. time plots for these processes (Figure 15 and Figure 16) were used to calculate the difference between the initial final energy, giving the value of the activation energy.
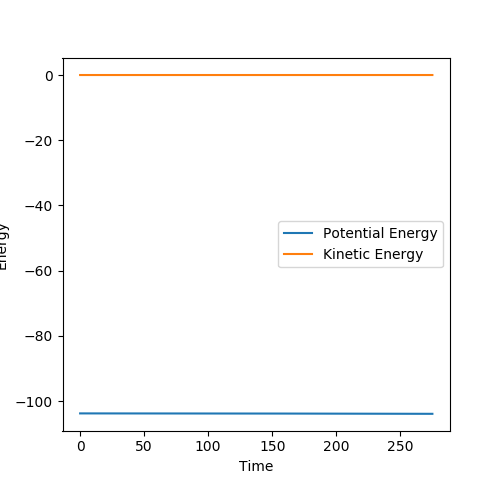
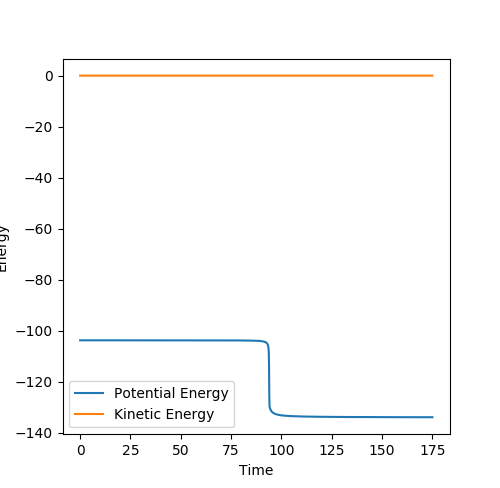
The activation energy for the reaction between F and H2 is 0.129. This is incredibly low, meaning that there is hardly a barrier to reaction. The activation energy for the reaction between H and HF is 30.158.0, as this reaction involves the breaking of the strong HF bond.
Jas213 (talk) 13:32, 28 May 2018 (BST) What number is that? Where are your units? You should have zoomed into the E vs. time plot with the small Ea, how else would you have found the value?
Release of reaction energy
The reaction between F and H2 is very exothermic, meaning that a lot of energy is produced during the reaction. This energy must be conserved, so is converted into vibrational energy in the products. The plot of Momentum vs. Time for a successful reaction (Figure 17) shows how the vibrational energy increases greatly after the reaction. This extra energy will be dissipated to other molecules via collisions, causing the kinetic energy of the molecules in the substance to increase. To confirm that this is the mechanism for release of the reaction energy, the temperature of the reaction could be monitored. Temperature is a measure of the kinetic energy of the molecules in a substance, so an increase in temperature would suggest that the reaction energy had been converted into vibrational energy and dissipated throughout the substance.
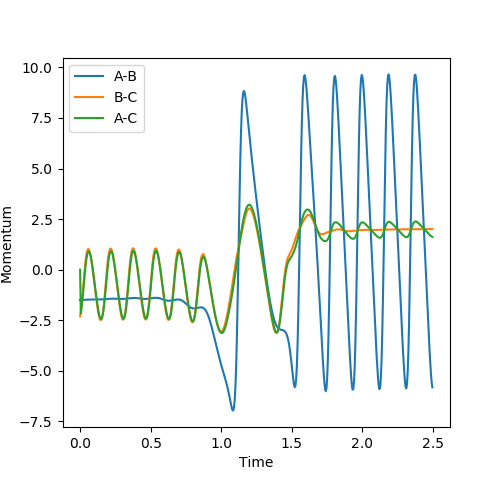
Polanyi's empirical rules
Jas213 (talk) 13:38, 28 May 2018 (BST)Subsequently you use at least one p higher than -3, where is your answer to the exercise in which you vary the momenta between -3 and 3?
Polanyi's rules give guidelines on how energy should be distributed between translational vs. vibrational energy to allow for a successful reaction.[4] They state that, for a reaction with a late transition state, vibrational energy is more effective at pushing the reaction to completion than translational energy. As the reaction between F and H2 has an early transition state, the energy of the transition state is close to that of the reactants, so little energy is needed to cause a reaction. Polanyi's rules would suggest that for a successful reaction to occur, the translational energy of the reactants should be greater the vibrational energy of the H2 molecule, as little energy is needed to break the H2 bond. Figure 18 shows an example of a successful reaction, where the translational energy is greater than the vibrational motion.
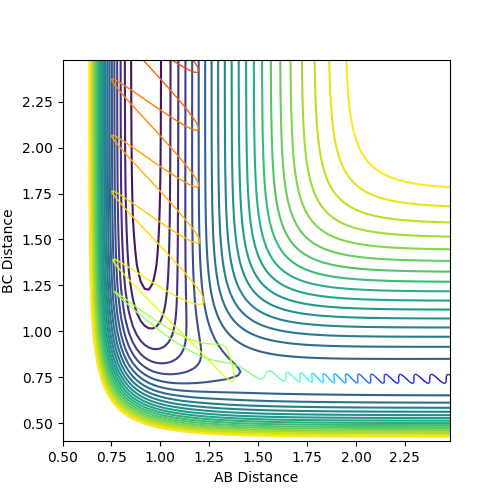
Jas213 (talk) 13:34, 28 May 2018 (BST) Very good illustration of your understanding of Polanyi's rules.
On the other hand, the reaction between H and HF has a late transition state, so the energy of the transition state is much higher than that of the reactants. Polanyi's rules suggest that a successful reaction will occur when the vibration energy of HF is greater than the translational energy of the reactants, as the high vibrational energy will be needed to break the strong HF bond. An example of a successful reaction with these conditions is shown in Figure 19.
However, there are cases where a successful reaction occurs with conditions that don't obey Polanyi's rules, as they are only guidelines. For example, Figure 20 shows a successful reaction between F and H2 where the vibrational energy is greater than the translational energy.
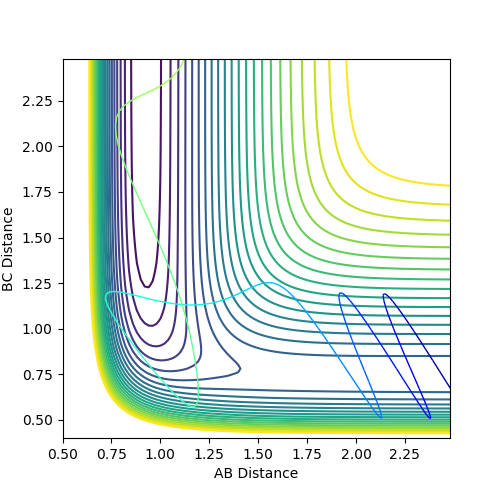
Figure 21 shows a successful reaction between H and HF where the translational energy is greater than the vibrational energy.
Jas213 (talk) 13:37, 28 May 2018 (BST) Sudden ending, how would you explain your last observation? What's your overall conclusion?
References
- ↑ T. Bligaard, J.K. Nørskov, in Chemical Bonding at Surfaces and Interfaces, 2008
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: 2006
- ↑ Stephen J. Blanksby, G. Barney Ellison, Bond dissociation energies of organic molecules, 2002
- ↑ Zhaojun Zhang, Yong Zhou, DOng H. Zhang, Gábor Czako, Joel M. Brown, J. Phys. Chem. Lett., 2012, 3, 3416-3419.