MRD:pc2715
EXERCISE 1: H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
Both gradients of the potential energy at minimum and at the transition structure are both zero. The minimum point and the transition structure can be distinguished by using the curvature curve. If the trajectory starting position is on the transition point, it will be there forever. But a small change in the radius will cause a change in the potential energy, making it roll down the hill on either one side, reactant or the product. However, if it is in the minimum energy surface, it will at either end of the reaction, product or the reactant.
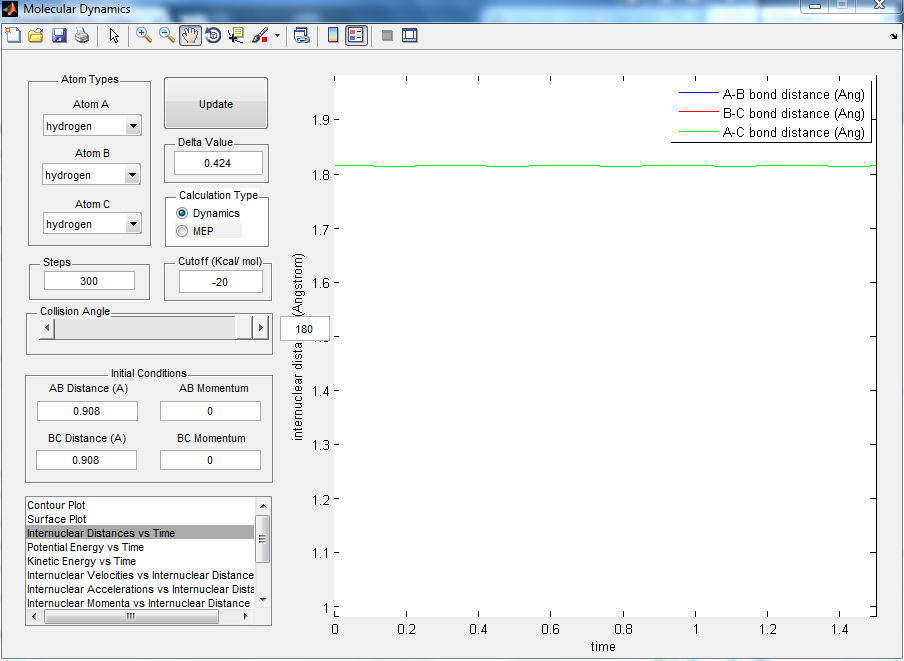
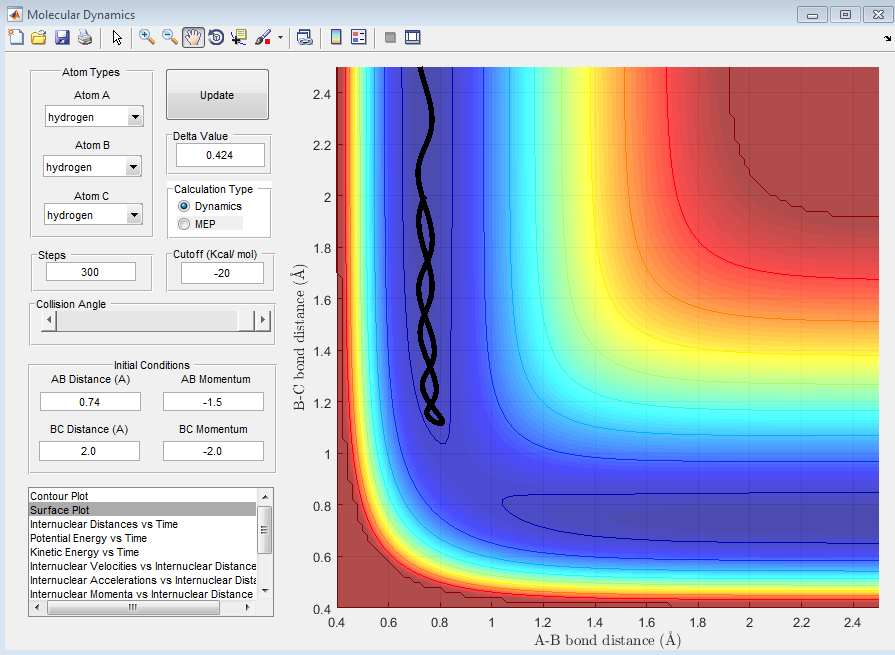
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
R of 1 and 2 is 0.908. The internuclear distances for both radii did not change with time. This means that the molecules are in a position where dV(r)/dr = 0 but it is not the minimium peak. It is where the transition state is as a small change in the position cause the change in energy level at only one way, toward the reactant or the product.
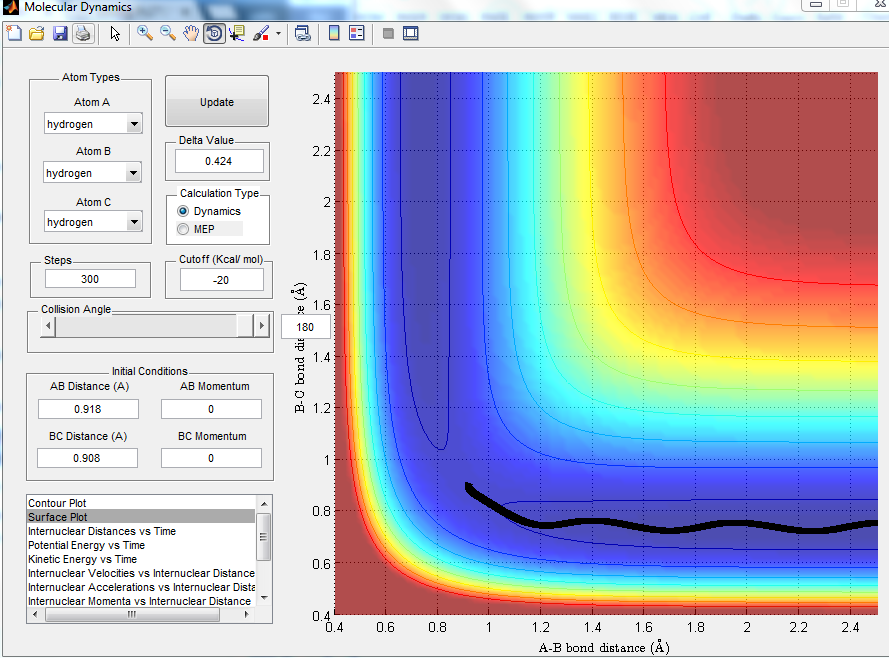
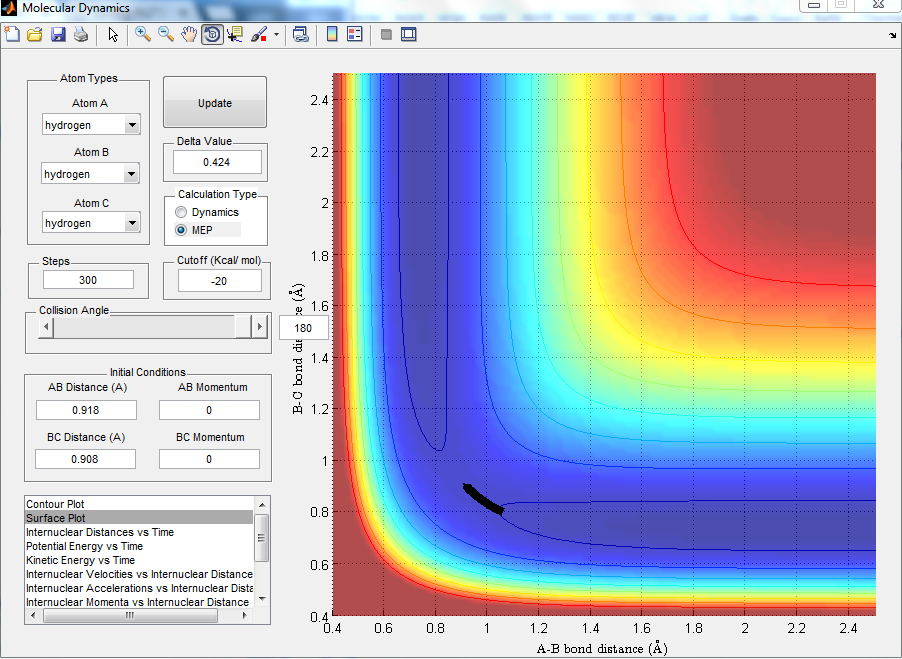
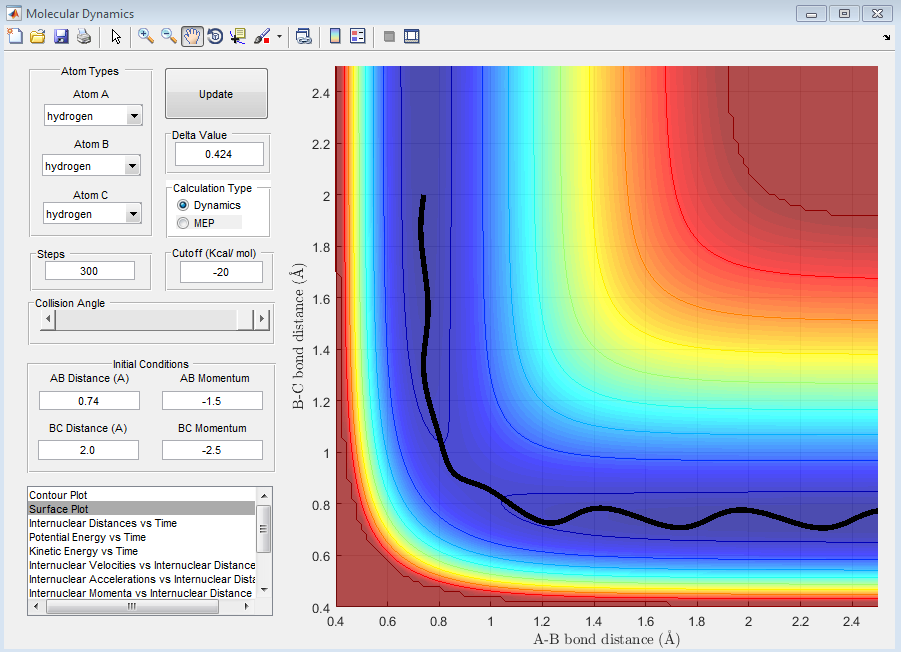
Comment on how the mep and the trajectory you just calculated differ.
MEP projection is much shorter and there is no oscillation as it corresponded to the infinitely slow motion. However, with dynamic calculation, oscillation was taken into consideration and the trajectory shown had more oscillation.
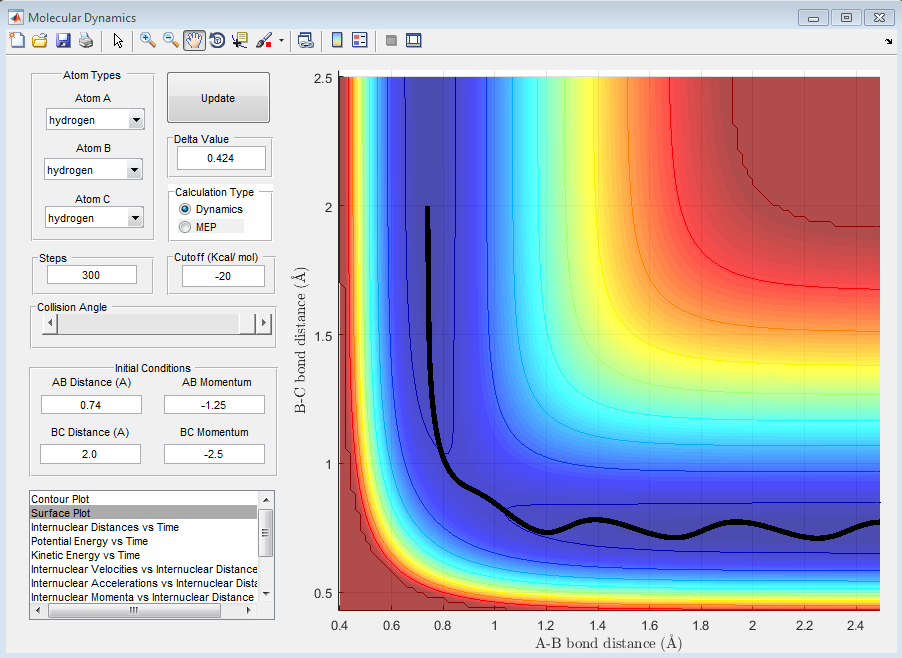
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| P1 | P2 | Description |
|---|---|---|
| -1.25 | -2.5 | Reactive- The energy is enough to move from the product to the reactant |
| -1.5 | -2.0 | Unreactive - The reactant don’t have enough energy to overcome the transition energy barrier |
| -1.5 | -2.5 | Reactive - There is enough energy to move from the the reactant to the product. |
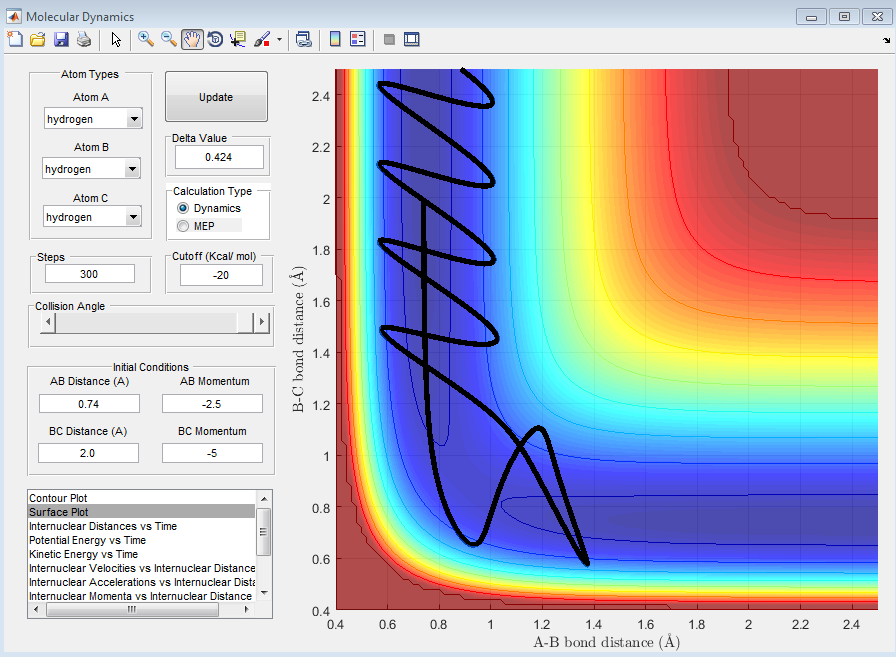
| -2.5 | -5.0 | Unreactive - Reactant have enough energy to overcome to barrier but it reverse toward the reactant because of barrier recrossing |
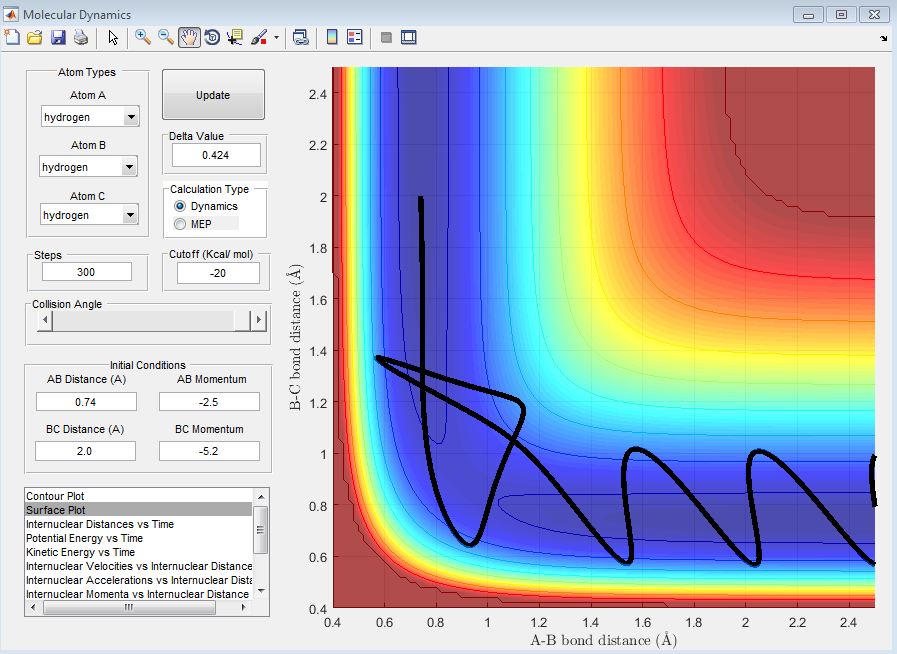
| -2.5 | -5.2 | Reactive - Overall reaction is reactive even though the reaction went back to the reactant for a short time. The high momentum push the reaction toward the product. |
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The main assumptions of Transition State Theory are; the reactants do not need to be in a correct orientation for the reaction to occur, every collision have enough energy to overcome the energy barrier, and the successful collision rate is 100%. The prediction rate value will be higher than the experimental value as the experimental do not have a 100% successful rate and so the rate of turning into product will be lower than expected.
Problem 2, F - H - H system
===Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state.===
H + HF is endothermic and H + F2 is exothermic. This is due to the fact that H-F bond is a lot stronger than H-H. The energy needed to break H-F is more than the energy release from making H-F, making H + HF reaction endothermic. However, in H + F2, the energy used to break F-F will be less than the energy released when H-F formed, making H + F2 reaction exothermic. Transition start position: Distance (H-F/AB) = 1.815 Distance (H-H/BC) = 0.745 The activation energy for H + HF and H + F2 are 0.5 kcal/mol and 30.5 kcal/mol.
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A set of initial conditions that results in a reactive trajectory is AB(HF) = 2.10 Å, BC(HH) = 0.75 Å, p(AB) = -2.12, and p(BC) = 2.38. From looking at the Internuclear Momenta vs Time, a transfer of energy between translational and vibrational energy was observed. The released energy was transfer to the vibrational energy in the created H-F bond. This can be confirmed by looking at the oscillation of H-F (A-B) after the transition state.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state
Polanyi’s empirical rules tells that the translational energy is more effective in increasing the efficiency of the reaction than the vibrational state for the early transition state. The opposite can be applied to the late transition state. F + H2 When transitional energy is small at -0.5 and vibrational energy is large at 2, the reaction is unsuccessful. However, if the condition were changed to a large transitional energy, at -0.8, and small vibrational energy at 0.1, the reaction become successful. This means that F + H2 as an early transition state. H + HF When transitional energy is small at 1.5 and vibrational energy is small at -0.5, the reaction is unsuccessful. However, if the condition were changed to a smaller transitional energy, at 0.1, and larger vibrational energy at -2.1, the reaction become successful. This means that F + H2 as an late transition state.