MRD:ny517
Molecular Reaction Dynamics
Exercise 1: H + H2
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is defined as the maximum energy point on the minimum energy path and the point on the potential energy surface when the gradient (partial first derivative) of the potential is equal to zero (∂V(ri)/∂ri=0). The transition state can be identified as a saddle point which means it has a partial second derivative greater than and less than zero (dependant on the variables and direction of axis). A local minimum is the point where it is solely a minimum and so the second derivative is always a positive value.
(Good.) Cq3417 (talk) 22:40, 6 June 2019 (BST)
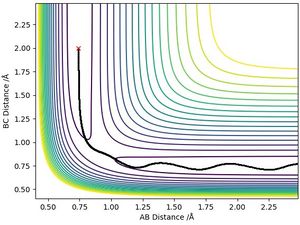
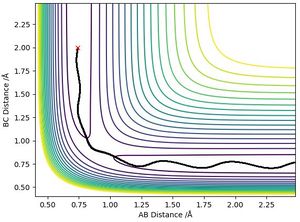
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
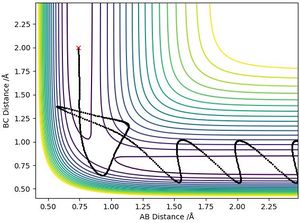
The best estimate of the transition state to 3 decimal places was: rts=r1=r2= 0.908 Å
This was estimated through looking at the contour plot of the initial conditions set for a H + H2 reaction and following the reactive trajectory to the point where r1 was approximate to r2 - which was in the region of 0.9 Å (as seen on the contour plot below). This is because for a system with identical atoms, the equidistant point is equal to the transition state position. After trialling values in this region, 0.908 Å produced a trajectory with a constant internuclear distance between both atoms (as seen on the plot below) indicating that the trajectory will not fall off the ridge. This is a transition state since the atoms are stationary over time when they have no initial momenta.


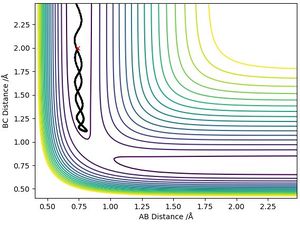
Comment on how the mep and the trajectory you just calculated differ.
The mep produces a trajectory that follows the valley floor and is also known as the reaction path. It shows a straight-line path along this trajectory because the velocity is always reset to zero after each time step. This does not provide a realistic account of the motion of atoms during the reaction since it assumes the atoms have no mass. The “Dynamics” calculation provides a more realistic trajectory since it accounts for the mass of the system and so the motion of the atoms in the gas phase will be inertial. In a MEP, kinetic energy is assumed to be 0 which explains why there are no oscillations along the path. As the potential energy decreases towards its minimum from the transition state, there is no kinetic energy producing a momentum and causing the molecule to travel up the potential energy curve at small bond distances so it remains at the potential energy minimum resulting in no oscillations.
(Good explaination.) Cq3417 (talk) 22:40, 6 June 2019 (BST)


If the initial conditions were reversed, the A-B and B-C plots would switch for the “Distances vs Time” and “Momenta vs Time” graphs. This is because the magnitude of the forces in the reaction do not change but the direction does. As the time increases, the A-B distance increases whilst the B-C bond distance stays constant (bar slight oscillations) at 0.75 because atom A is travelling further away from the BC diatomic molecule. At 5 seconds the A-B bond distance is 18 Å. As the time increases, the A-B momentum plateaus at 2.5 kg ms-1 whilst the B-C momentum oscillates about an average of 1.25 kg ms-1. If the values were reversed, the B-C bond distance would increase whilst the A-B bond distance would remain constant.


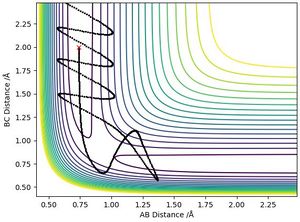
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
Initial positions r1 = 0.74 Å and r2 = 2.0 Å
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.0 | Yes | Reactants travel through transition state then start to vibrate | Plot 1 |
| -1.5 | -2.0 | -100.4 | No | Reactants do not overcome activation energy and rebound off the transition state. Atoms vibrate on approach and after reaching transition state | Plot 2 |
| -1.5 | -2.5 | -98.9 | Yes | Reactants vibrate whilst travelling through transition state then vibrate more vigorously | Plot 3 |
| -2.5 | -5.0 | -85.0 | No | Reactants pass through transition state then pass back through the transition state to reform the reactants | Plot 4 |
| -2.5 | -5.2 | -83.4 | Yes | Reactants travel through transition state, then reform reactants and pass through the transition state again. This occurs with strong vibrations throughout reaction | Plot 5 |
(Maybe next time try to label under the plot.) Cq3417 (talk) 22:40, 6 June 2019 (BST)
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory (TST) is used to qualitatively understand the reaction rates of elementary chemical reactions with the idea that all reactions occur through a transition state. One assumption is that once the reagents gain an energy sufficient enough to overcome the activation energy, they will react to form the product. In reality this is not the case as is seen in the calculated examples above where some reactants reached the transition state but reformed the reagents and not the products. This is because of another assumption of TST which is that the energy is looked at classically rather than quantum mechanically so fails to account for the quantization of molecular vibrations. Failing to factor this is why TST predictions for reaction rates will typically be higher than experimental values.
(Good, but any reference?) Cq3417 (talk) 22:40, 6 June 2019 (BST)
EXERCISE 2: F - H - H system
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic).
F + H2
H-H distance: 0.74 Å
F-H distance: 2.00 Å
H-H momentum: -1.5 kg ms-1
F-H momentum: -2.5 kg ms-1
The reactants are higher in energy than the products therefore the reaction is exothermic.
H + HF
F-H distance: 0.74 Å
H-H distance: 2.00 Å
F-H momentum: -1.5 kg ms-1
H-H momentum: -2.5 kg ms-1
The reactants are lower in energy than the products therefore the reaction is endothermic.
How does this relate to the bond strength of the chemical species involved?
Through inspection of the potential energy surfaces, it is clear that the bond strength of H-F is greater than the bond strength of H-H since more energy is needed to break the H-F bond in the second reaction.
Locate the approximate position of the transition state.


H-H distance: 0.745 Å
H-F distance: 1.815 Å
To find the transition state, both momenta were set to equal zero. Hammond's postulate states that the transition state of a reaction resembles either the reactants or the products, to whichever it is closer in energy. The transition state will be closer in energy to the reactants of the exothermic (first) reaction and the products of the endothermic (second) reaction. The contour plot shows the atoms do not fall off the ridge and the Internuclear Distances plot shows the distances remained constant (bar slight oscillations).
Report the activation energy for both reactions.
The activation energy is defined as the difference in energy between the reactants and transition state. The energy of the transition state is known, which is -103.752 kcal mol-1. 0.3 A was added to and subtracted from the HF bond length to calculate the minimum energy difference between the reactants and transition state for both reactions. The reactant energies were extracted using an mep calculation. The calculated activation energies are stated below:
- For the F + H2 system: 0.236 kcal mol-1
- For the H + HF system: 30.256 kcal mol-1
Reaction Dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
For a F + H2 reaction trajectory:
H-H distance: 0.744832 Å
H-F distance: 2.00 Å
H-H momentum: -0.7 kg ms-1
H-F momentum: -1.6 kg ms-1


It is seen that the B-C momentum plateaus over time due to the H2 bond being split and the H atoms becoming further apart so the bond vibrations begin to stop. The A-B momentum oscillates as the B-C momentum stops oscillating which is due to the H-F atom being formed. The H-F bond vibrations are larger than the H-H bond vibrations due to the strength of the bond being greater and hence a have a higher enthalpy of formation. If the H-F bond is stronger than the H-H bond then this will result in an exothermic reaction. This could be confirmed experimentally through a reaction calorimeter. The plot displaying energy over time indicates that the total energy is constant and hence conserved. It also shows that the the potential and kinetic energy convert between each other as the atoms vibrate between their bonds. Notice that the energy oscillations become larger after the transition state- similar to that seen in the momentum plot.
(Do you mean 'hence have a'?) Cq3417 (talk) 22:40, 6 June 2019 (BST)
Changing momenta:
- Keeping the same initial conditions but changing the H-H momentum:

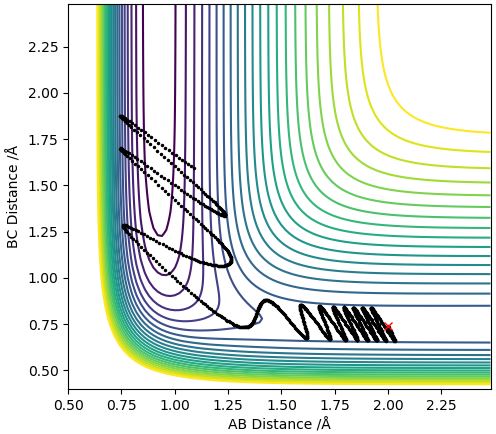





Only when pHH was equal to -1 and -2 kg ms-1 was there a reaction trajectory. When the time step was doubled for pHH=0 a reaction trajectory was produced indicating that the H2 bond was broken and a HF bond was formed. For the other reactions, the reactants passed the transition state but went back and reformed the reactants.
When pFH = -0.8 kg ms-1 and pHH = 0.1 kg ms-1, a reaction trajectory occurs:
For the reverse reaction, H + HF:
The initial conditions are set with :
H-H distance: 2.00 Å
H-F distance: 0.74 Å
H-H momentum: -0.59 kg ms-1
H-F momentum: -6.55 kg ms-1
Keeping the atom positions constant, the momenta were varied to have a low vibrational motion on on the H-F bond and an arbitrarily high value of pHH above the activation energy and obtain a reactive trajectory:
H-H distance: 2.00 Å
F-H distance: 0.74 Å
H-H momentum: -7.55 kg ms-1
F-H momentum: -0.35 kg ms-1
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The efficiency of a reaction is dependant on the position of the transition state. If there is a late transition state, the vibrational energy is the most influential on the efficiency of the reaction and hence its ability to overcome the reaction energy. If there is an early transition state, the translational energy is the most influencial on the efficiency. Using this, it can be deduced that for the endothermic H + HF system, the reaction is affected more by the vibrational energy and that for the exothermic F + H2 system, the reaction is affected more by the translational energy.
(Good, but any reference?) Cq3417 (talk) 22:40, 6 June 2019 (BST)