MRD:nk2018

Molecular Reaction Dynamics Lab

Exercise 1: H + H₂ System

What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

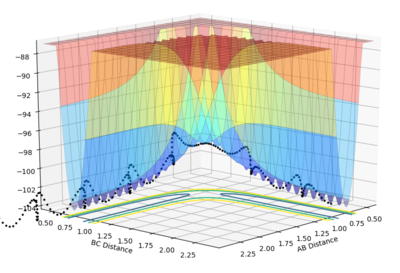
The energy surface shown above represents the relative energy of the molecules as the reaction progresses. It can be seen that for the transition state and minima the potential energy gradient with respect to r₁ and r₂ is 0. The transition state is a saddle point, hence it is a local minimum in one plane but a local maximum in another plane. (Using planes here is not correct. A TS is a maximum in one direction (the reaction coordinate) and a minimum in the orthogonal coordinate. Fjs113 (talk) 14:38, 3 June 2018 (BST))

However for the minima any perturbation will cause an increase in energy, hence the minima correspond to stable species, i.e. the reactants and products.

The minima and transition state can be distinguished mathematically. The first derivative of both the minima and the transition state will be equal to zero. However if you take the second partial derivatives ∂²V(r₁)/∂r₁ and ∂²V(r₂)/∂r₂. For the minima the second derivatives in both directions will be greater than zero (minimum). However for the transition state one derivative will be greater than zero (minimum) and one will be less than zero (maximum).

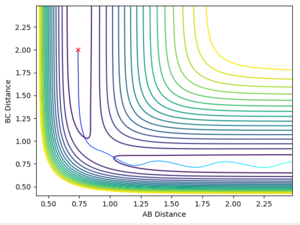
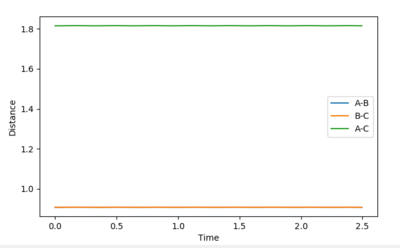
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

After setting the momentum to zero and setting the distances r₁ equal to r₂ the distance can then be varied until the lines in the internuclear distance vs time plot flatten. This is significant because at the transition state the atoms will not be oscillating. My value for the transition state position, r_ts, is 0.9075 Å.

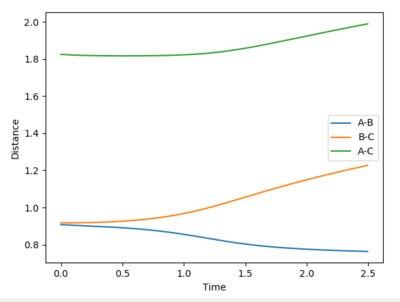
Comment on how the mep and the trajectory you just calculated differ.

Calculation Type	Dynamics	MEP
Contour Plot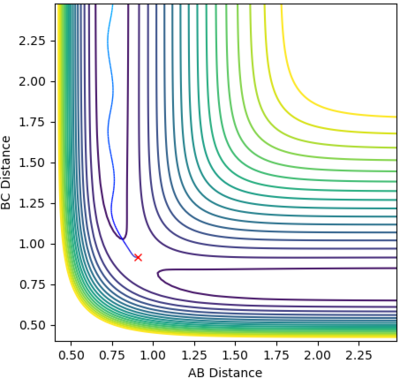
Internuclear Distances vs Time
Internuclear Momenta vs Time

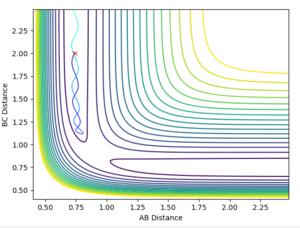
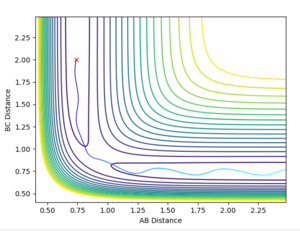
The reaction path (minimum energy path or mep) is a type of trajectory that corresponds to infinitely slow motion, this means the velocity always reset to zero in each time step. So for the MEP you do not observe the vibrational energies and hence the oscillations and not observed. The MEP shows the lowest energy path whereas the dynamic shows a truer path taken including the vibratonal energies. This can be seen in the contour plots as for the dynamics plot it oscillates whereas in the MEP it is a smooth line. If you change the & final positions around, the result would the a mirror the graphs shown above. The graphs would just run in the opposite direction.

(This is all ok, but you really need to proof read your report. There is a staggering number of typos here! Fjs113 (talk) 14:38, 3 June 2018 (BST))

Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

p1	p2	Total Energy / kcal	Reactive?	Contour Plot	Comments
-1.25	-2.5	-99.018	Reactive		The atoms are moving with the correct momentum to pass the transition state and form the products
-1.5	-2.0	-100.456	Non-reactive		The atoms are not moving with enough kinetic energy in order to overcome the activation energy and hence simply collide but do not react.
-1.5	-2.5	-98.956	Reactive		The atoms are moving with enough energy in order to overcome the activation energy and hence can pass the transition state to form the products.
-2.5	-5.0	-84.956	Non-reactive		The molecules momentum in this case is too large. In the collision the atoms form a bond, but repels due to coulombic repulsion. Hence the molecule crosses the transition state again in a process known as 'recrossing'. It results in large oscillations.
-2.5	-5.2	-83.416	Reactive		In this case again the molecules collide with high momentum and crosses the transition state twice but in this it results in a reaction and the products are formed. It also results in large oscillations.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory assumes that the nuclei behave according to classical mechanics. It also assumes that the reactions have one saddle point, and hence one transition state, that must be passed over. The theory works well at lower temperatures but at the higher temperatures due to recrossing some reactions that pass the transition state it still may not react. Hence the observed rate of reaction is slightly lower than that predicted by the theory. The theory also does not consider quantum mechanical effects such as tunneling.

EXERCISE 2: F - H - H system

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The reaction between F and H₂ is exothermic, this can be seen in the downhill gradient of the surface plot. The total energy decreases from the reactants to the products. The bond dissociation energy of H₂ is 432 kJ mol^-1 whereas the bond dissociation energy of HF 562 kJ mol^-1 . Hence the HF molecule is more stable than the H₂ and hence energy is released and the reaction is exothermic. For H + HF to form H₂ and F is a very endothermic reaction. However a proton transfer reaction given enough momentum is feasible.

F + H2 → HF + H	H'F + H → H' + HF

(What you're meant to explore here is H + HF -> H2 + F and not the proton transfer. Fjs113 (talk) 14:38, 3 June 2018 (BST))

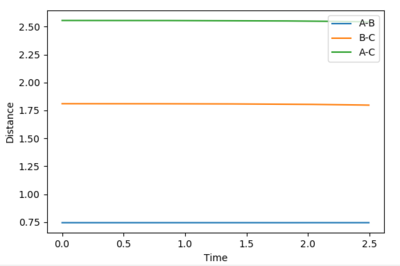
Locate the approximate position of the transition state

Again the values for r₁ and r₂ were varied until no oscillation was observed in the internuclear distances vs time plot, ie. the lines were flat. The values for r₁ was 0.744 Å and the value for r₂ was 1.811 Å. It can be seen that the r₁ bond length similar to that of the H-H, this is because the transition state energy is more similar to the reactants than the products. Hence the structure is more similar to that of the reactants than the product.

Report the activation energy for both reactions.

Using an MEP calculation type by slightly displacing the transition state the activation energy could be calculated. The relative activation energies show the relative feasibility of the reaction.

Reaction	Approximate Activation Energy (kcal mol-1)
F + H2 → HF + H	0.2
HF + H → F + H2	30

(How did you calculate these numbers? You need to show your working. Fjs113 (talk) 14:38, 3 June 2018 (BST))

F + H2 → HF + H	HF + H → F + H2

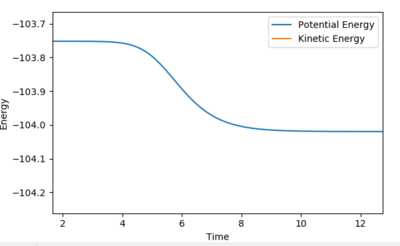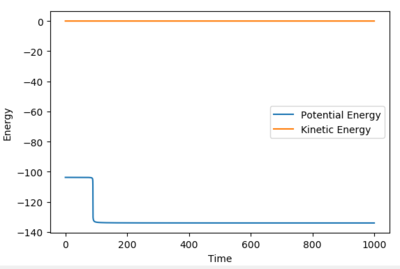Identify a set of initial conditions that results in a reactive trajectory for the F + H₂

The set of conditions used were A-B= 0.74, B-C= 2.3, pAB= 0 pBC=-2, it can be seen from the contour plot that under these conditions it is reactive.

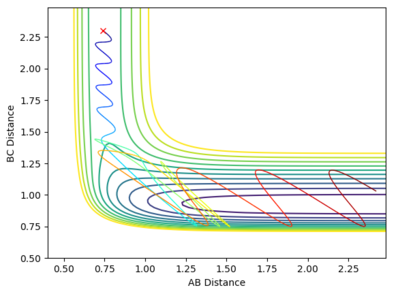
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The conservation of energy can be seen from the internuclear momenta vs time graph. As the reaction is very exothermic energy must released in the form of kinetic energy. This can be seen in the larger oscillations after the reaction. This can be confirmed experimentally via both temperature change and IR.

(You need to give some more detail here. Fjs113 (talk) 14:38, 3 June 2018 (BST))

PFH	PHH	Contour	Reactive
-0.5	-3		Unreactive
-0.5	-2		Unreactive
-0.5	-1		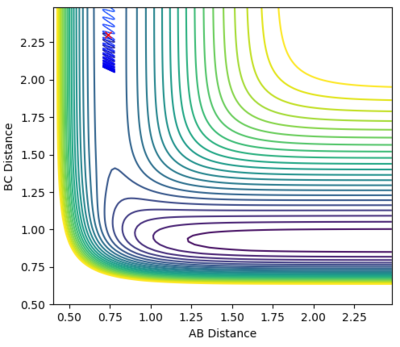Unreactive
-0.5	0		Unreactive
-0.5	1		Unreactive
-0.5	2		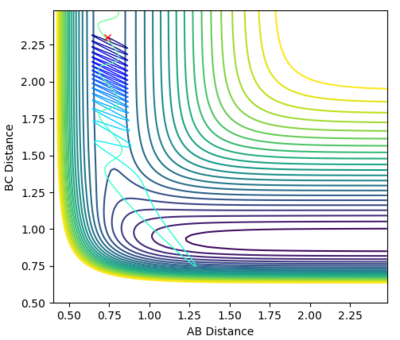Unreactive
-0.5	3		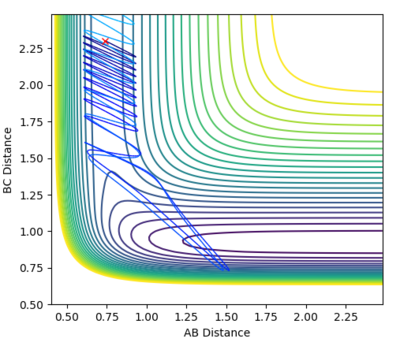Unreactive

PFH	PHH	Contour	Reactive
-0.8	0.1		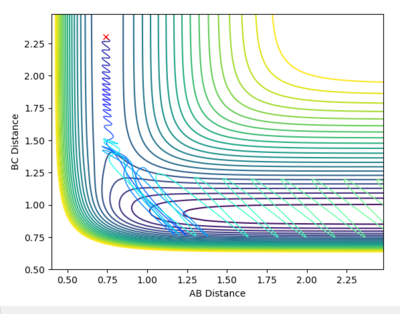Reactive

As this is an exothermic reaction it has an early transition state, and hence it can be seen that according to Polanyi's rules it is more dependent upon the translational energy than the vibrational energy . This can be seen as only slightly altering the translational momentum resulted in a reaction whereas drastically changing the vibrational energy had no effect, as seen in the contour plots above.

H + HF

PFH	PHH	Contour	Reactive
-8.5	-0.5		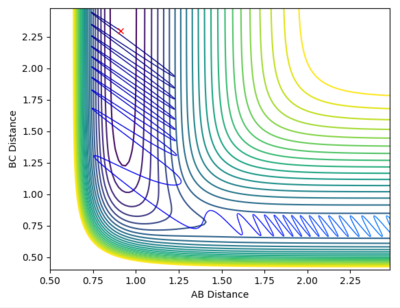Reactive

The F + H2 → H-F + H is endothermic and hence has a late transitional state. Again according to Polanyi's rules as this is a late transitional state and hence a lot of vibrational energy is required.

(Again, you need to elaborate a bit more. You also missed out on the last question! Fjs113 (talk) 14:38, 3 June 2018 (BST))