MRD:mz5717

H + H₂ SYSTEM

Transition State Determination

On a potential energy surface, the transition state is represented by a saddle point, which is mathematically defined as:

When the partial derivatives V_r1 and V_r2 both equal to 0 at a point, if the value of (V_r1r1V_r2r2 - V²_r1r2) < 0 at that same point, then it is a saddle point.

Alternatively we can identify it by computing the second partial derivatives, V_r1r1 and V_r2r2. For a saddle point, one of them will be positive and the other one negative.

Additionally, when (V_r1r1V_r2r2 - V²_r1r2) > 0, the point represents a local maximum/minimum. It is a local maximum if V_r1r1 < 0, or a local minimum if V_r1r1 > 0.

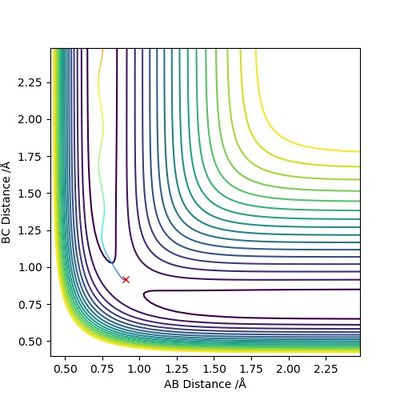
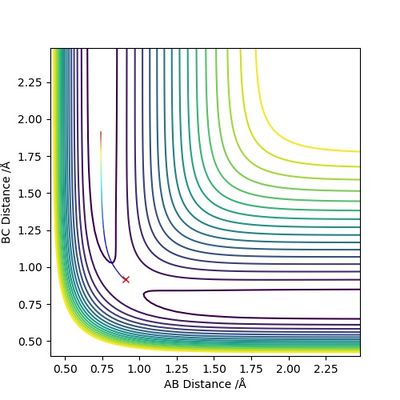
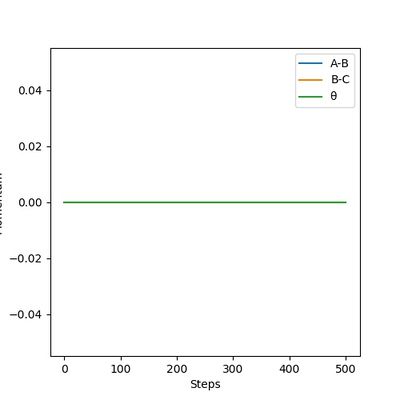
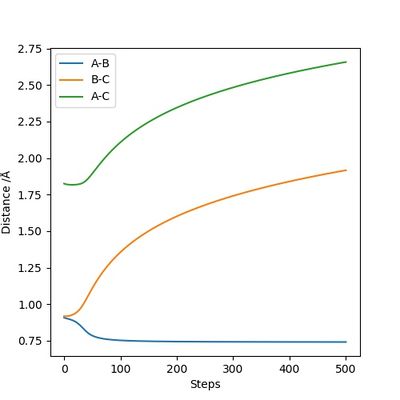
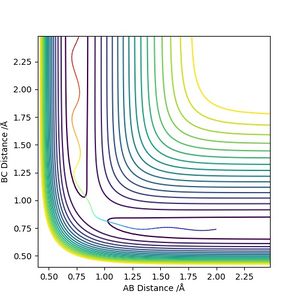
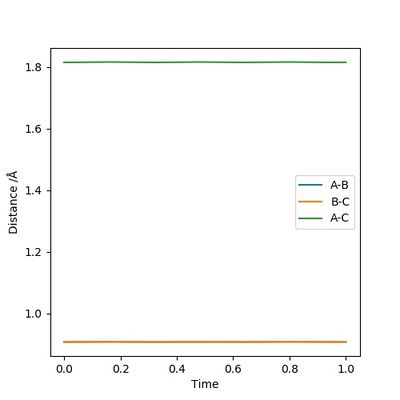
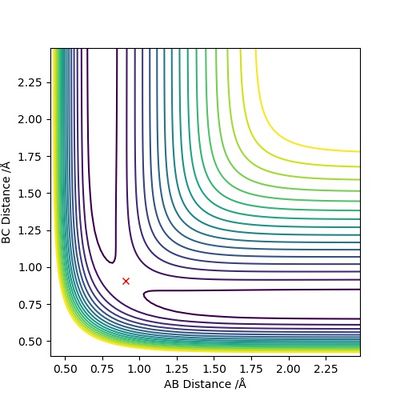
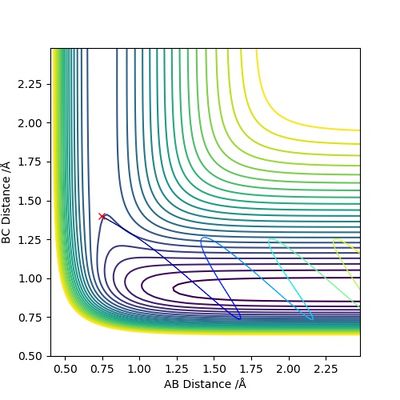
The transition state position is estimated to be 0.90743 Å. i.e. r₁ = r₂ = 0.90743 Å, p₁ = p₂ = 0. When subjected to this initial condition, the internuclear distances do not vary with time because the equilibrium established at the saddle point does not provide driving force for any forward or backward reaction.

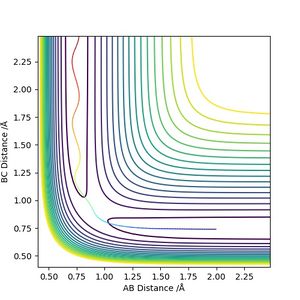
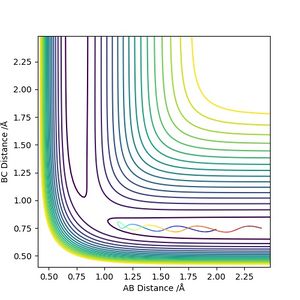
This is illustrated with the plot below. The contour map shows the position of the TS with a cross.

(Reasonable description of the transition state and good illustration of plots) Cq3417 (talk) 15:37, 15 May 2019 (BST)

Figure 1: time-variation of internuclear distances.

Figure 2: contour map of the potential energy surface showing the position of the TS.

Reaction Trajectories

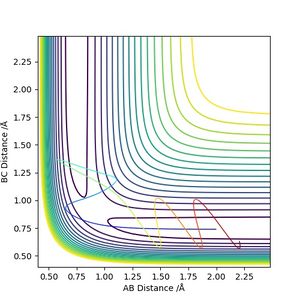
Dynamics and MEP are two methods of calculating the reaction trajectory. The table below compares the outcomes produced by these two methods.

Dynamics (r1 = 0.90743, r2 = 0.91743, p1 = p2 = 0)	Figure 3: reaction trajectory produced by Dynamics.	Figure 4: time-variation of momenta produced by Dynamics. Blue curve shows the momentum oscillation of the new bond.	Figure 5: time-variation of internuclear bond length produced by Dynamics. Blue curves shows the bond length oscillation of the new bond.	The Dynamics calculation accounts for the conversion of kinetic energy to vibrational energy, as shown by the oscillating momentum and bond length of the new bond formed.
MEP (r1 = 0.90743, r2 = 0.91743, p1 = p2 = 0)	Figure 6: reaction trajectory produced by MEP.	Figure 7: time-variation of momenta produced by MEP. There is zero motion.	Figure 8: time-variation of internuclear bond length produced by MEP. The length of the new bond stays constant.	The MEP calculation does not account for the bond vibration, therefore the momentum of the newly formed molecule is a straight line, and there is no oscillation in the new bond.

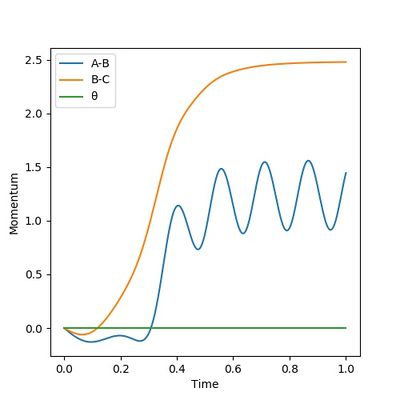
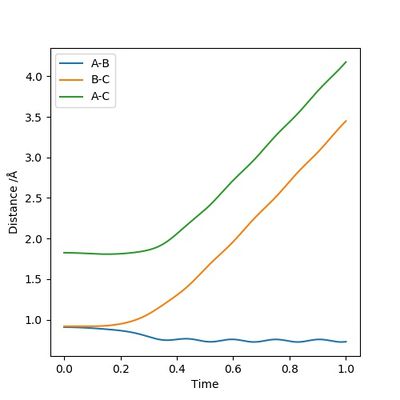
According to Figures 4 and 5, we set the initial conditions to be r₁ = 0.74895, r₂ = 1.0 (an arbitrary large distance), p₁ = -1.2745, p₂ = -2.4889, which corresponds with the final position of the trajectory only with the signs of the final momenta reversed. The resulting trajectory is almost the same as those we obtained previously.

(Good explanation.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

Figure 9: initial conditions corresponds to the final values of the above trajectory but with the signs of the momenta reversed. A very similar reaction path.

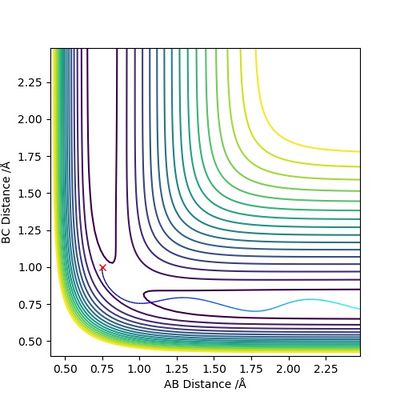
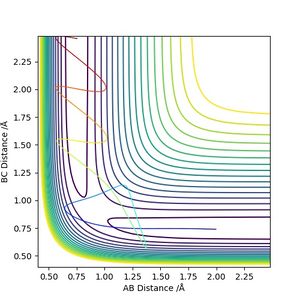
Next, we examine the effect of initial momenta and total energy on the reaction trajectory, i.e. if it is reactive or not, by giving the reactants varying amounts of initial momenta. The results are summarized by the table below.

p1	p2	Etot	Reactive?	Reaction path	Description of the dynamics
-1.25	-2.5	-99.018	Y		More internal vibration after the transition state; energy sufficient to pass over Ea.
-1.5	-2.0	-100.456	N		Reaction does not proceed; the molecules bounce back without reacting.
-1.5	-2.5	-98.956	Y		Considerable internal vibration before & after reaching the TS; more than enough energy to overcome Ea.
-2.5	-5.0	-84.956	N		The kinetic energy supplied is way above the activation energy so the reaction path goes past the saddle point. However it bounces back after a while, with most of the energy contributed to intramolecular vibration. So the starting materials ARE reactive and we do have products formed, but they eventually turn back to the reactants.
-2.5	-5.2	-83.416	Y		Reaction proceeds to the formation of the products with much of the kinetic energy contributing to the internal vibration of the newly formed product.

(Excellent illustration though additionally showing the energy vs time plot can make it better.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

Transition State Theory

The main assumptions of Transition State Theory are:

- The nuclei behave classically

- The reaction path passes through the saddle point representing the transition state

- Once the reaction passes through the TS, it will proceed to the formation of the product(s)

Under most circumstances, TST matches with experimental results to a good extent. However, from the simulation we can conclude that when the kinetic energy supplied is way above the activation energy, this is not necessarily the case. Here the experimental position of the transition state may largely deviate from the theoretical one represented by the saddle point on the potential energy surface. Because of the abundance of energy supplied, more molecules are able to occupy vibrational modes of higher energy, making their motion more complicated and harder to predict. This could be the underlying reason for the large deviation. It could be hard as well to predict the reaction rate under such circumstances; for example, when there is a

reverse reaction going on.

(I think you may need to cite the description of this assumption.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

F - H - H SYSTEM

Transition State Determination

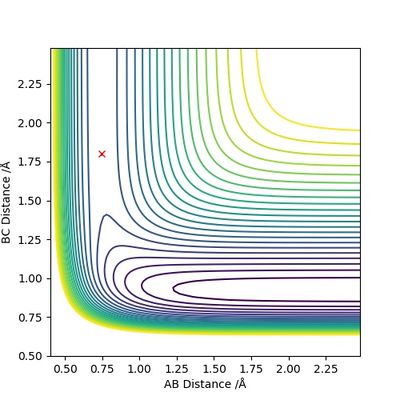
F + H₂ --> H + HF is exothermic and has an early TS. The reaction releases energy because the new H-F bond formed is stronger than the H-H bond broken (F is much more electronegative than H). On the other hand, H + HF --> F + H₂ is endothermic and has a late TS. The reaction requires input of energy because the H-F bond broken is much stronger than the H-H bond formed.

Setting initial momenta to be both zero, the position of the TS is estimated to be r₁ = 0.745 Å and r₂ = 1.80 Å.

(Good, nice and clear.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

Figure 10: position of the TS marked by a cross.

Figure 11: no bond length variation when at equilibrium.

Activation Energy

Figure 12: reaction profile of H + HF --> F + H2.

Figure 13: reaction profile of F + H2 --> H + HF.

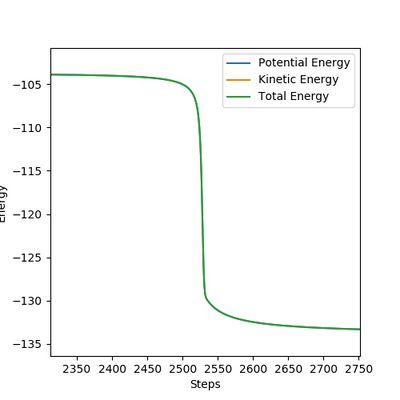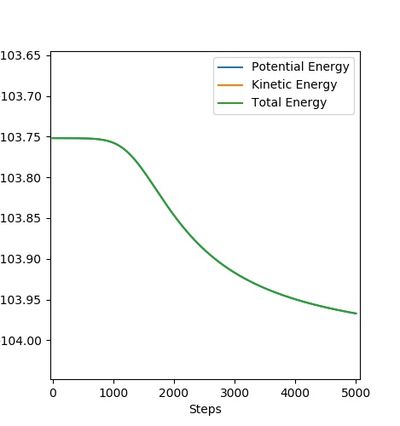The figures above show the energy profiles of H + HF and F + H₂ respectively.

The activation energy of H + HF is determined as -103.867 - (-133.257) = 29.390 kcal/mol

The activation energy of F + H₂ is determined as -103.752 - (-103.967) = 0.215 kcal/mol

(How you get this plot is my question so I think you need to discuss this in detail.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

Energy Distribution

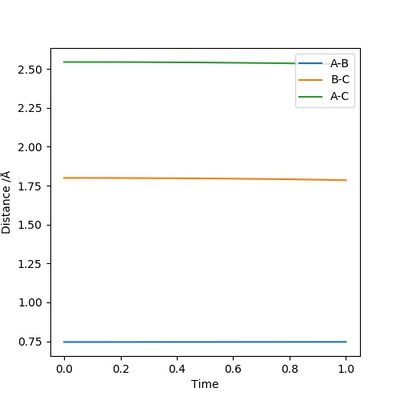
First we focus on energy conversion. Below is a general case of a successful reaction.

Figure 14: a generic reactive path with r1 = 0.745, r2 = 1.40, p1 = 3, p2 = -0.5.

Figure 15: corresponding time-variation of momenta of this reaction path.

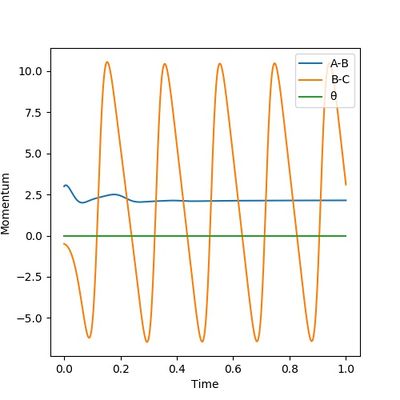Figure 15 shows that the vibration of bond A-B gradually ceases, which means that bond A-B corresponds to the H-H bond broken. In this case bond B-C must be the new H-F bond formed. The H-F bond continues its vibration and eventually becomes the only source of momentum, which means that the excess kinetic energy from the F atom was converted to vibrational energy after the reaction has occurred. The extent and modes of the H-F bond vibration can be measured by Raman spectroscopy.

(It can be more clear if you include the energy vs time plot here.) Cq3417 (talk) 15:37, 15 May 2019 (BST)

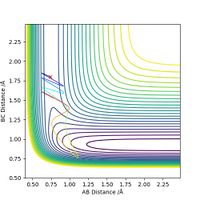
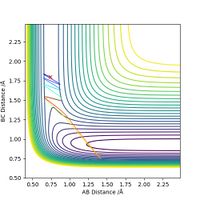
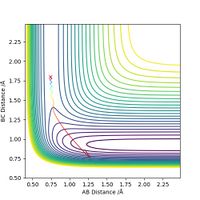
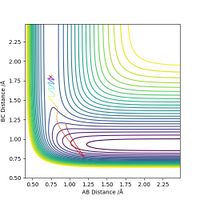
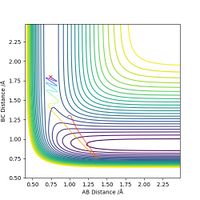
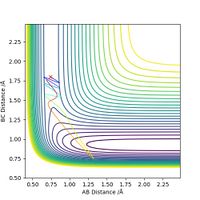
Next, for the reaction F + H₂ --> H + HF, we set the initial conditions to r_HH = 0.74, r_HF = 1.80 and p_FH = -0.5. Different values of p_HH, ranging from -3 to 3, are tested and the results are summarized in the table below.

pHH = -3	pHH = -2.4	pHH = -1.8	pHH = -1.2	pHH = -0.6
pHH = 0	pHH = 0.6	pHH = 1.2	pHH = 1.8	pHH = 2.4	pHH = 3

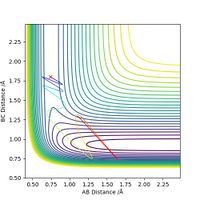
The table shows that when p_HH has a value between -1.2 and 0, the reaction proceeds to the product side. In all other cases the reaction trajectory more or less bounces back to the reactant side, and the extent of this backward conversion increases as the absolute values of p_HH increases. The only outlier is p_HH = 2.4, where the trajectory generally stays on the product side.

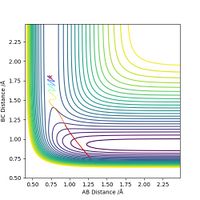
Now increase p_HF slightly to -0.8, and largely reduce p_HH to 0.1. The trajectory below shows that despite having considerably lower total energy, the reaction still proceeds to the product side.

Figure 16: p_HF = -0.8, p_HH = 0.1, r_HH = 0.74, r_HF = 1.80. The total energy of the system has been significantly reduced.

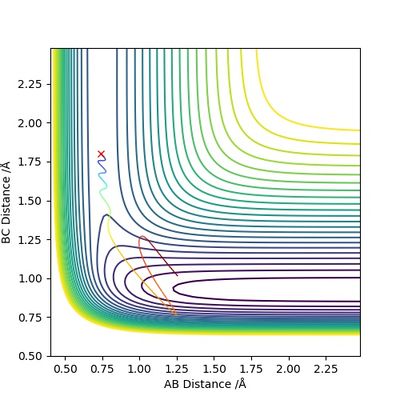
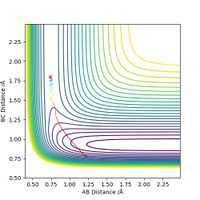
Finally, for the reaction H + HF --> F + H₂, we assume that there is very little vibration within the H-F bond (i.e. p_HF = 0.2), and that the H atom is approaching with extremely high kinetic energy (p_HH = 5). With the initial conditions r_HH = 0.745, r_HF = 1.80, the trajectory below is obtained. It is evident that the high kinetic energy possessed by the H atom is initially able to break the H-F bond and push the system to the product side; however, HF is reformed afterwards and then the entire process repeats. This is an oscillating reaction.

Figure 17: r_HH = 0.745, r_HF = 1.80, p_HF = 0.2, p_HH = 5. This set of initial conditions results in an oscillating reaction.

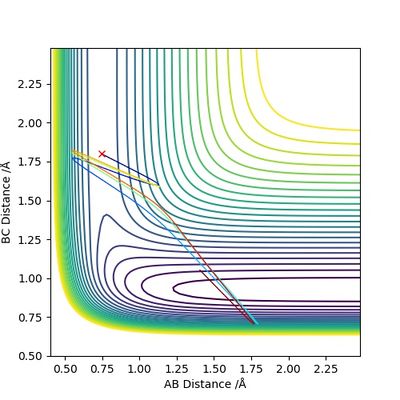
By decreasing p_HH and increasing p_HF, it is possible to obtain a reactive trajectory. For example, when we let other variables stay constant and change the rest to p_HF = 0.3, p_HH = 2.6, the reaction can indeed proceed to the product side as shown in the figure below.

Figure 18: when r_HH = 0.745, r_HF = 1.80, p_HF = 0.3, p_HH = 2.6, we obtain a reactive trajectory.

(Where is your discussion that respects to the Polanyi's empirical rules?) Cq3417 (talk) 15:37, 15 May 2019 (BST)

In conclusion, a proper distribution of kinetic and vibrational energy is crucial for the trajectory to be reactive. Generally in most cases, a high kinetic energy nearly guarantees a reactive path. The reaction F + H₂ --> H + HF has an early TS, and does not need much energy to reach it; the other reaction H + HF --> F + H₂ has a late TS, and requires much higher vibrational energy to reach it. The second reaction also shows us that just having high kinetic energy is not enough to trigger a successful reaction. By lowering the kinetic energy and increasing the vibrational energy we see that there is a delicate balance between the two that eventually leads to a reactive trajectory.

(Overall this is a sufficient report that shows a good understanding of this concept. However, the citation of reference and, the combination of theories and experimental data are required to be noticed.) Cq3417 (talk) 15:37, 15 May 2019 (BST)