MRD:mtc3018
Exercise 1: H + H2 system
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is located at a saddle point on a PES, which can be mathematically expressed as:
.
This means that a transition state is the maximum point along the minimum energy path in a PES. The first two equations listed above mean that the force registered at the transition state is 0, while the last equation distinguishes the point from a local minimum. The equation represents the determinant of the Hessian matrix and is a requirement for a saddle point.
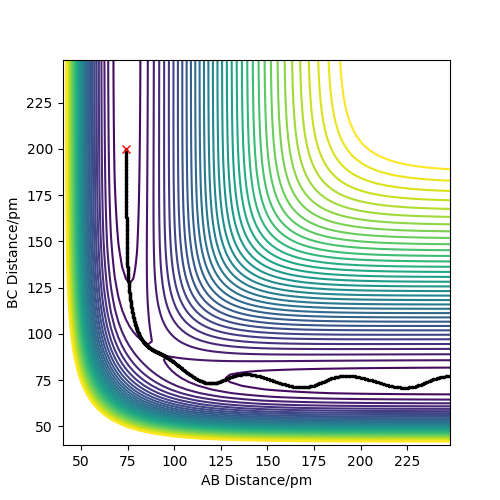
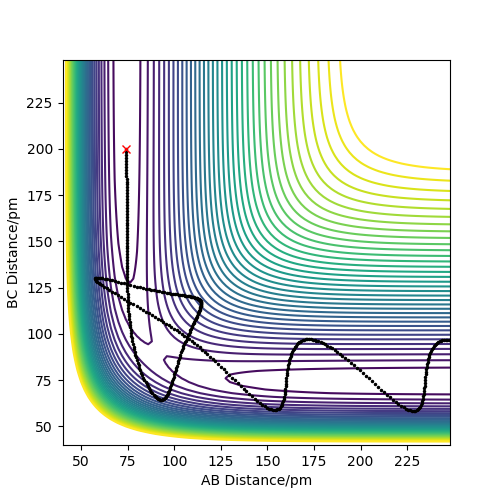
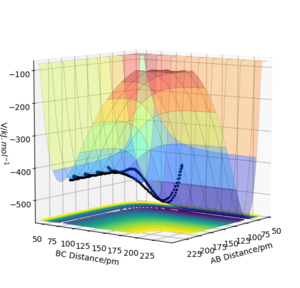
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
The transition state position was found by looking for the value of r (which is the separation between the three atoms: rts = rAB = rBC) for which the force is 0 and for which the one of the vectors in the Hessian matrix points up and one points down. Because the system is symmetric, consisting of 3 identical atoms, rAB = rBC at the transition state. Additionally, at the transition state, no oscillations are registered, as the system reaches an equilibrium, losing its vibrational energy. This is illustrated in the "Internuclear Distance vs Time" plot.
rts was found to be 90.774 pm.
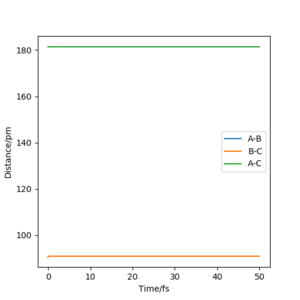
Good. Pu12 (talk) 19:36, 21 May 2020 (BST)
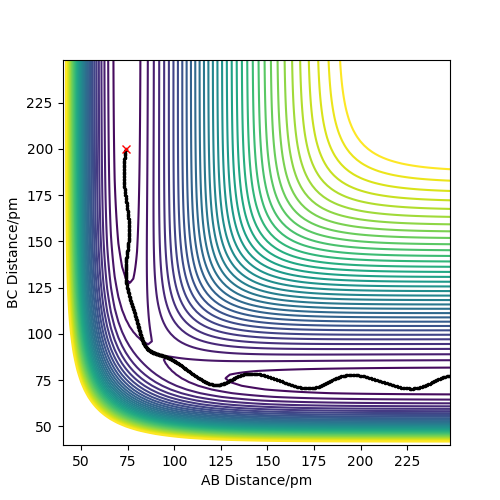
Comment on how the mep and the trajectory you just calculated differ.
The minimum energy path was found by changing the initial conditions such that r1 = rts+1 pm, r2 = rts and p1 = p2 = 0 g.mol-1.pm.fs-1. This allowed finding the steepest descent path from the transition state to the products (H3+ H2-H1), as r1 (r(H2-H3)) was slightly increased compared to r2.
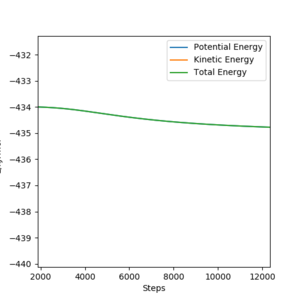
When running the calculation using the dynamics calculation type, a more detailed description of the motion along the minimum energy path is obtained. This is because MEP does not take vibrational energies into account, which is the reason why the path is not oscillating, while the one corresponding to the dynamics type is. Additionally, MEP does not allow the atoms to accumulate kinetic energy with each step, resetting the velocity of atoms to 0 after calculating their direction. Overall, it can be concluded that in the dynamics calculation the total energy of the system is conserved, while in the MEP algorithm, because the kinetic energy is constantly reduced to zero, while the potential goes down, the total energy of the system drops.
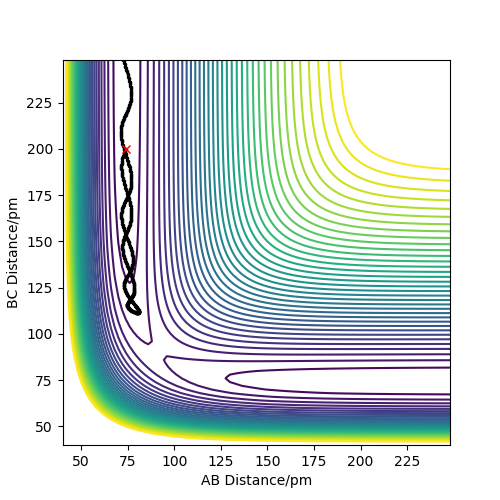
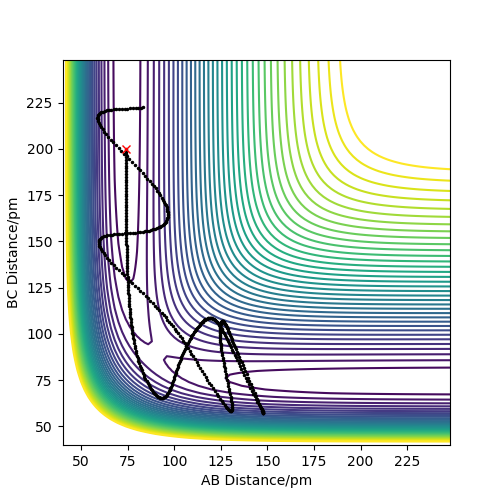
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
Initial positions: r1 = 74 pm and r2 = 200 pm
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Reactive | H3 approaches the H1-H2 molecule and collides with it, forming the H2-H3 molecule which moves in the direction of the original molecule, while H3 returns in the opposite direction. The collision leaves the new molecule in a higher vibrational excited state, as the oscillations increase. | 
|
| -3.1 | -4.1 | -420.1 | Not reactive | The atom and molecule move towards each other, however after the collision they bounce off and change their momenta going opposite way. The velocity corresponding to r2 increases with time, but the H1-H2 velocity remains constant, the molecule oscillating slightly. | 
|
| -3.1 | -5.1 | -414.0 | Reactive | The dynamics is very similar to the original case, however the momentum of the H1-H2 molecule is higher now and the molecule oscillates more. After the collision, the newly created molecule has an even higher vibrational energy. | 
|
| -5.1 | -10.1 | -357.3 | Not reactive | H3 approaches the molecule with high velocity and collides with it, which keeps the middle atom at roughly the same position while H3 bounces off it a few times, causing large oscillations. The last collision leaves the middle atom with a high enough momentum to increase the interatomic distance such that it reaches H1 and binds to it. This is again causing large oscillations and both the original molecule and the atom travel in opposite directions. | 
|
| -5.1 | -10.6 | -349.5 | Reactive | This situation is similar to the previous one, however, now, H3 has enough energy to recross the energy barrier and hold on to H2. H1 goes back in the direction where it cam from, while the new molecule has very high vibrational energy. | 
|
Contrary to the hypothesis that for a reaction to occur it is only required that kinetic energy overcomes the activation barrier, more aspects come into play when deciding whether a reaction is successful or not. The trajectory of the reaction thus needs to be studied, as the way the atoms oscillate is crucial in forming a bond by passing the transition state and remaining on that side of it. As it can be seen in example 4, although the transition state energy was passed, the extra energy is used to recross the barrier and the trajectory goes back on the initial path. Therefore, the information in the table demonstrates that the above assumption is incorrect. You haven't discussed transition state theory or commented on how rates predicted by it would differ from those in your examples. Pu12 (talk) 19:36, 21 May 2020 (BST)
EXERCISE 2: F - H - H system
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 → HF + H is exothermic, because the HF bond corresponds to a lower potential than an H2 bond. This can be seen in a potential energy surface plot where the potential is lower for a small AB (HF) distance than for a small BC (H2) distance. Conversely, HF + H → F + H2 is endothermic.
This can be rationalised by inspecting bond enthalpies. The H-F bond is stronger (565 kJ/mol) than the H-H bond (432 kJ/mol), which means that when going from H-H to H-F energy will be released, while energy is needed to go from H-F to H-H.
Good. Pu12 (talk) 19:36, 21 May 2020 (BST)
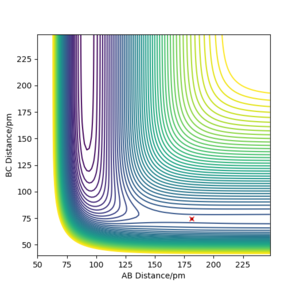
Locate the approximate position of the transition state.
As for the previous example involving 3 hydrogens, the transition state was found by setting both momenta to 0 and finding the values of rAB and rBC for which the forces that act along AB and BC are 0. The vectors in the Hessian also need to point to both upwards and downwards. This happened when rAB =rHF=181.1 pm and rBC=rHH=74.49 pm. This transition state is obviously no longer symmetric because different atoms are involved.
The values for the interatomic distances make sense when thinking about Hammond's postulate, which says that the transition state resembles the structure which is closer in energy. Due to the fact that HF + H → F + H2 is endothermic, the structure corresponding to an H2 bond (short BC distance) is higher in energy and therefore closer to the transition state energy. This is why, when searching for the transition state, the distances associated with the higher energy geometry need to be considered.
Report the activation energy for both reactions.
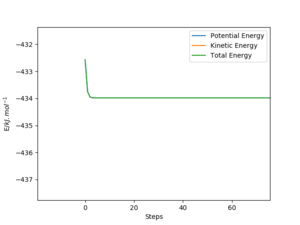
Activation energy results from the difference in energy between the transition state and that of the reactants. MEP calculations allow us to find this difference, as the kinetic energy is set to 0 and the potential energy can be determined. An energy vs. time plot was used.
For finding the activation energy of the reaction F + H2 → HF + H, the momenta were set to 0 and the interatomic distances were set to rAB =rHF=rts+1=182.1 pm and rBC=rHH=74.49 pm. The difference between the initial and final energy is ~0.6 kJ/mol.
For finding the activation energy of the reaction HF + H → H2 + F, the momenta were set to 0 and the interatomic distances were set to rAB =rHF=181.1 pm and rBC=rHH=rts+1=75.49 pm. The difference between the initial and final energy is ~1.5 kJ/mol This value is much too low and should be around 120-130, it looks like you might have got the energy for the first reaction twice, you should double check the contour plots to see that the trajectories in the calculations you use to find the activation energy correspond to the correct reaction. Pu12 (talk) 19:36, 21 May 2020 (BST)
.
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
A reactive trajectory was chosen for F + H2 → HF + H such that: rAB =rHF=175 pm, p=-1.5 g.mol-1.pm.fs-1 and rBC=rHH=rts+1=75.49 pm, p=2 g.mol-1.pm.fs-1. The trajectory on the PES plot shows large oscillations following the collision of the F atom with the H2 molecule, which was also described in the animation: the original molecule vibrates considerably, however the collision with the slow F atom leaves the system in a very high vibrational state. This means that a large amount of the energy of the system is converted from potential to kinetic.
Experimentally, the energy release can be detected via calorimetry, as well as spectroscopy. The IR spectrum would show overtones and the new molecule would be vibrationally excited. Over time, the IR spectrum would show an increase in intensity for the peak going from the 0th vibrational state to the 1st and a decrease in the intensity of the other peaks .
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules stress on the importance of translational energy, rather than vibrational in getting a successful exothermic reaction. At the same time, for an endothermic reaction to occur, it is more important that the system has vibrational energy, rather than translational.
The reaction F + H2 → HF + H is exothermic and therefore translational energy is more effective for overcoming the barrier Which is at an early transition state. Pu12 (talk) 19:36, 21 May 2020 (BST) . However, the reaction has a low activation energy so a too high energy of the system might result in an unsuccessful reaction.
The reaction HF + H → H2 + F is endothermic and happens more readily when a high vibrational energy is provided, having a late transition state. You should reference Polanyi's rules. Good report overall but with some correctionsPu12 (talk) 19:38, 21 May 2020 (BST)