MRD:mpg15
Excercise 1: H + H2
Transition States vs Minima
At both the transition state and a minimum, the total gradient of the potential energy surface is zero. To distinguish between the two, we must look at the second derivatives along both axes. A minimum will be found at the coordinates where:
fxxfyy - f2xy > 0 and fxx > 0 and fyy > 0
A saddle point, which corresponds to a transition state, will be found at the coordinates where:
fxxfyy - f2xy < 0
Therefore, a minimum in the potential energy surface will have increasing gradients in all directions, while a transition state will have an increasing gradient in some directions and a decreasing gradient in others. [1]
(Fv611 (talk) 10:57, 30 May 2017 (BST) Yes. Well done on mentioning the second derivative test)
Locating the Transition State
The estimated position of the TS is 0.90775A. At this point, the animation displayed no change in particle position, and the AB/BC bond distance plot is completely flat. 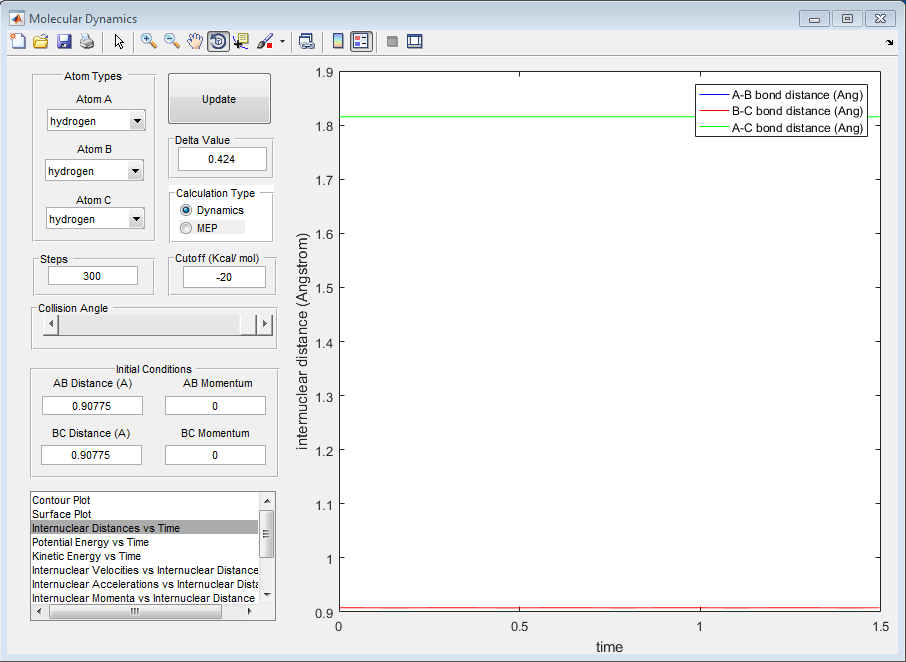
(Fv611 (talk) 10:57, 30 May 2017 (BST) Why is there no change in position at the TS?)
MEP vs Dynamics Calulation
The mep trajectory gives a perfectly straight line rolling down the minimum of the slope, while the trajectory calculated using the dynamics method gave an oscillating path, showing the vibration of the molecule itself. If the BC distance is set to be off equillibrium, instead of the AB distance, the reaction moves towards the products instead of back towards the reactants. Setting up a calculation with the final positions set as the initial positions, and with the reverse sign of the final momenta as the initial momenta gives a plot of a standard reaction path.
(Fv611 (talk) 10:57, 30 May 2017 (BST) You describe the effects but not the cause. Why are they different?)
Reactive and Unreactive Trajectories
The table is given below:
| p1 | p2 | Reactivity |
|---|---|---|
| -1.25 | -2.5 | Reactive |
| -1.5 | -2.0 | Unreactive |
| -1.5 | -2.5 | Reactive |
| -2.5 | -5.0 | Unreactive |
| -2.5 | -5.2 | Reactive |
In the first set of initial conditions, the reaction proceeds smoothly, with small oscillations of the reactant and product molecules.
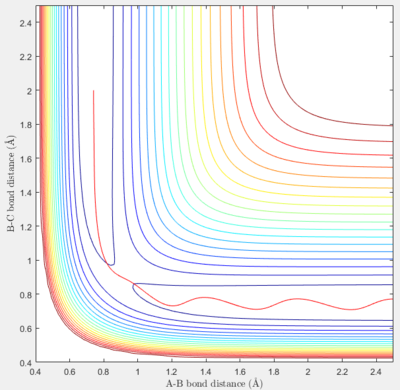
In the second set of initial conditions, the reaction does not run to completion - the reactants lack the energy to climb past the transition state energy barrier, and so a product never forms.
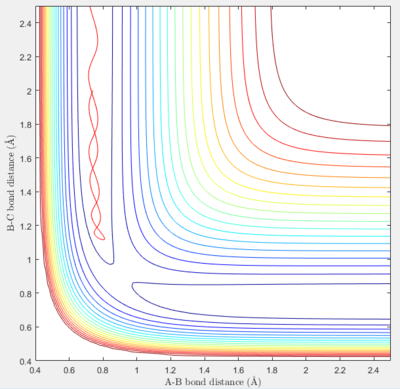
In the third set of initial conditions, the reaction also proceeds rather smoothly, with greater oscillation of the reactant and product molecules due to the increased energy of the system.
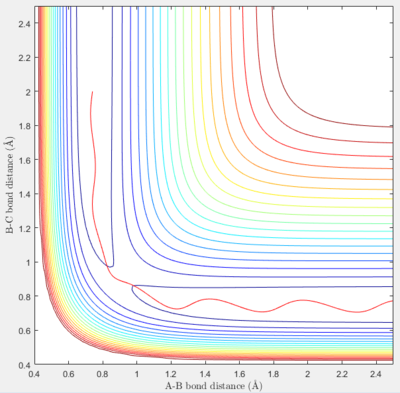
In the fourth set of initial conditions, the reaction shows more erratic behavior, with a very brief formation of the product and a reversion back to the reactants, which now display significant oscillations.
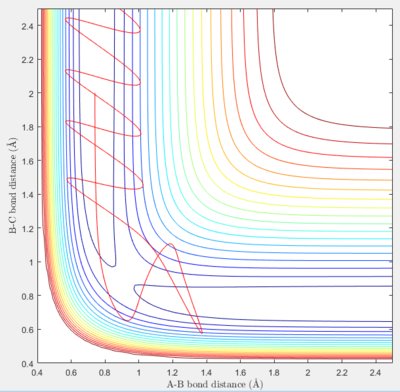
In the fifth set of initial conditions, the reaction runs to completion, whilst also displaying erratic behavior. The product forms, and a reversion back to the reactants is briefly seen, after which the product is reformed. The product shows very strong oscillations.
Transition State Theory
The key assumptions of transition state theory are that particles behave in a classical way with no quantum behaviour, and that the transition state can only be crossed once by the reaction trajectory. The latter demonstrably does not apply in all cases, as there are many reaction trajectories which pass more than once through the transition state. This means that the experimentally measured reaction rate would be lower than that predicted by the theory. The assumption that no quantum behaviour is observed is also incorrect, especially for small atoms such as hydrogen. Quantum tunnelling of electrons will play a significant part in speeding up the reaction rate by essentially changing the shape of the potential surface. The overall discrepancy of the reaction rates predicted by the theory and measured experimentally therefore depends on the exact system studied.[2][3][4]
Exercise 2: F-H-H System
Inspection of the Potential Energy Surface
Reaction Energetics
The F + H2 reaction is exothermic, due to the formation of HF, which forms stronger bonds and therefore has a lower potential energy.
The HF + H reaction is endothermic, due to the need to break the strong HF bonds.
(Fv611 (talk) 10:57, 30 May 2017 (BST) You provide no justification to your statements.)
Transition State Position
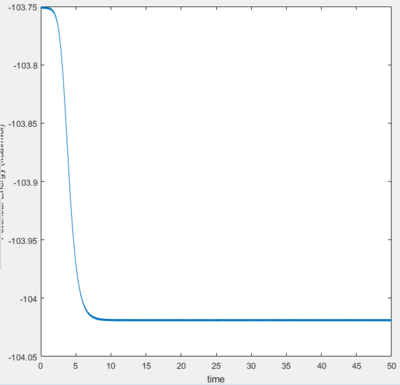
The transition state of the reaction is located at the point where the H-H separation is 0.7426, and the H-F separation is 1.8120. It has an energy of -103.75 Kcal/mol.
(Fv611 (talk) 10:57, 30 May 2017 (BST) Again, no justification)
Activation Energies
The activation energy for the F + H2 reaction is around 0.27 Kcal/mol
The activation energy for the HF + H reaction is around 30.15 Kcal/mol

(Fv611 (talk) 10:57, 30 May 2017 (BST) Again, no justification. Why should I believe your statements if you provide no evidence?)
Reaction Dynamics
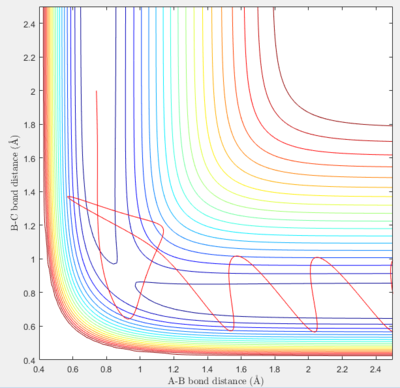
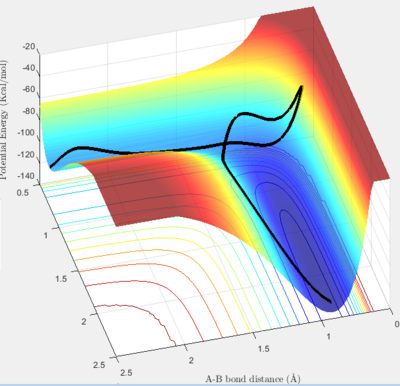
A reactive trajectory was generated, with the F-H separation set as 2.4A and the momentum as -0.8,and the H-H separation set as 0.74A, with the momentum as -0.3. This produces a trajectory which moves between products and reactants twice before a formation of a strongly oscillating FH molecule.
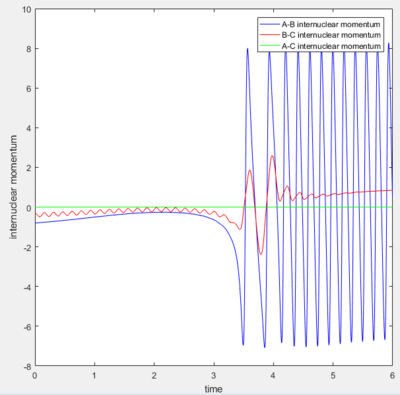
Reaction Energy Release
The potential energy of the reaction is converted into kinetic energy during the reaction. This energy is seen in the very large vibrational motion of the new molecule, as seen above. A part of that energy would also be transferred to the H atom which is freed during the reaction. The sharp increase in kinetic energy of the molecules would correspond to a large increase in temperature, which could be confirmed via experiment.
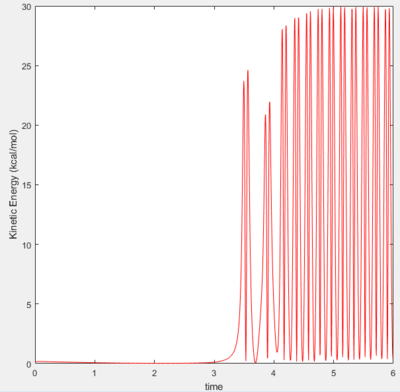
Setting initial HF separation and momentum as 2.4A and -0.5, with HH separation kept at 0.74, it was observed that momenta in the range -2.5<x<2.0 do not give a reactive trajectory, with the reactants never passing hte transition state. If the HF momentum is increased slightly to -0.8, even a HH momentum of 0.1 results in a reactive trajectory.
A reactive trajectory for a HF molecule was achieved with an initial HF separation of 0.9A, initial momentum of 2.8, HH separation of 2.4 and initial momentum of -7.4
Impact of Energy Distribution on Reaction Rate
Polanyi's empirical rules deal with the impact of the two types of motion - translational and vibrational - on endothermic and exothermic reactions. For the exothermic reaction, with an early transition state, it is the translational energy that drives the reaction, and therefore has the greatest impact on reaction rate. For the endothermic reaction, with a late transition state, it is the vibrational energy that drives the reaction and controls the rate.[5]
(Fv611 (talk) 10:57, 30 May 2017 (BST) Very little discussion and no examples. Also no mention of efficiency.)
References
1. P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 10th Editi., 2014.
2. J. Pineda and S. D. Schwartz, Phil. Trans. R. Soc. B, 2006, 1433–1438.
3. P. Pechukas and F. J. Mclafferty, J. Chem. Phys., 1973, 1622.
4. P. Pechukas and E. Pollak, J. Chem. Phys., 2008, 2062.
5. J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161–168.
