MRD:mlw115RXNDy

Exercise 1: H₂ + H system

Dynamics from the transition state region

Question 1. What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

Where a reaction is modeled on a potential energy surface the lowest energy path between the reactants and products is seen as a "valley floor" of the surface. The transition structure is a saddle point along the minimum energy ridge.

The gradient of the potential energy surface is zero at the minimum, along the direction of the reaction path and so the first derivative with respect to the inter-nuclear distance is zero. For the saddle point the gradient of the potential energy surface is zero orthogonal to the direction of the reaction pathway.

δV(r_i)/δr_i = 0

Second derivatives δV²(r_i)/δr_i² > 0 Minima δV²(r_i)/δr_i² < 0 Maxima

where V is the potential energy and r related to the nuclear positions.

The minimum pathway and saddle point can be distinguished using the second derivatives with respect to atom positions. The second derivative of a maximum point is negative, whereas the second derivative of a minimum is positive. As the saddle point is a maxima along the minimum path the second derivative is negative. The second derivative of the minimum energy path in the direction of the reaction will be positive.

Estimating Transition State Position

Question 2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Initial Conditions

	Distance	Momentum
AB	0.908	0
BC	0.908	0

Jas213 (talk) 20:00, 28 May 2018 (BST) Units missing.

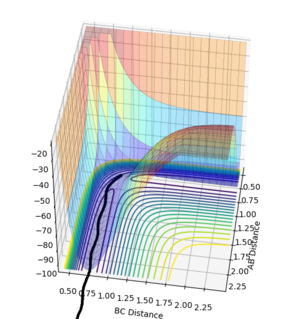
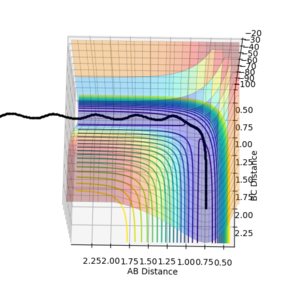
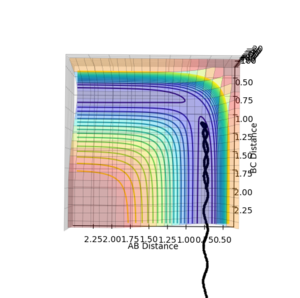
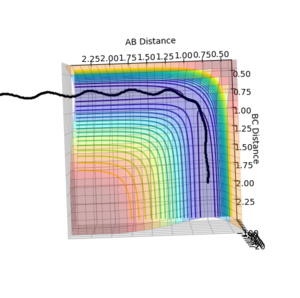
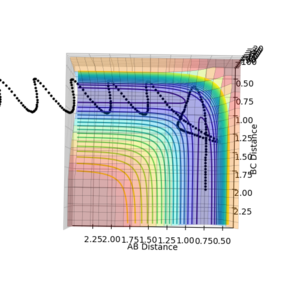
Surface Plot 1	Surface Plot 2	Internuclear distance vs Time
		|

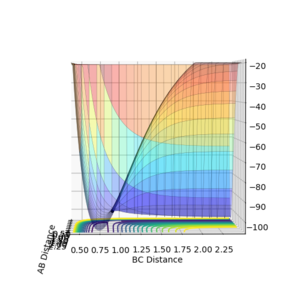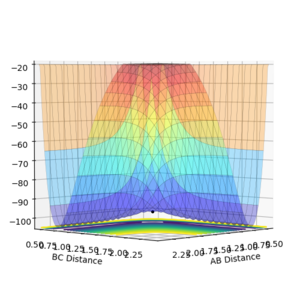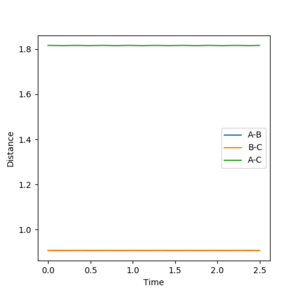The best guess of inter nuclear distances at the transition state was found using trial and error, to find the positions that would result in the minimum trajectory. As the system is symmetric the distances would be equal. The two surface plots are included to demonstrate the "reaction path". The internuclear distance vs time plot demonstrates no change in any bond lengths at the transition state so the overall momenta is 0 and potential energy is at the maximum. This agrees with that the transition state is a stationary point.

Reaction Path

MEP vs Dynamics

Initial Conditions

	Distance	Momentum
AB	0.909	0
BC	0.908	0

Surface Plot (MEP)	Surface Plot (Dynamics

Question 3. Comment on how the mep and the trajectory you just calculated differ.

It can be seen in the MEP plot that the trajectory follows the minimum energy valley floor without any obvious deviations or oscillation. This does not account for the inter-molecular vibrations between the molecules,. The MEP trajectory is corresponding to infinitely slow motion, it does not accurately represent the atomic motion of the reaction. The trajectory oscillates in the dynamics plot, also in much less steps the AB bond distance increases considerably more. This plot is more realistic as it accounts for the motion of atoms during the reaction.

Final Geometry

	Distance	Momentum
AB	9.993	0.754
BC	2.486	1.167

Reversed conditions

Initial Conditions

	Distance	Momentum
AB	9.993	0.754
BC	-2.486	-1.167

From taking the previous runs final conditions and setting these as the initial conditions and reversing the momenta values the reaction seems to run in reverse, reaching an end exactly at the transition state.

Determining Reactivity

Question 4. Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

Atoms	Internuclear distance
AB	0.74
BC	2.0

Jas213 (talk) 20:02, 28 May 2018 (BST) Again units missing everywhere, good that you stated the initial conditions, wouldn't have hurt to have a little introductory phrase instead of just copy pasting the questions.

pAB	pBC	Total Energy	Reactive?	Surface Plot	Explanation
-1.25	-2.5	-99.018	Yes		Initially the HAHB distance changes very little as the vibrational energy is quite low, as the HC approaches it can be seen that the BC distance decreases linearly. The molecules pass over the transition state, after this point the HAHB distance decreases and the HBHC distance oscillates slightly, with a higher vibrational energy than the HAHB molecule. This overall process represents the HAHB bond breaking and forming a HBHC molecule.
-1.5	-2.0	-100.456	No		The molecule approaches the maxima with some vibrational energy, shown by oscillations in the initial path, the energy of the system is not high enough to pass over the transition state energy maxima so the HC "rebounds" and the HBHC distance begins to increase. The HAHB molecule oscillations increase.
-1.5	-2.5	-98.956	Yes		The reaction proceeds similarly to the first case with HC approaching and forming a bond with HB as there is sufficient energy to proceed over the transition state maxima. The vibrational energy throughout is slightly higher than the first case, demonstrated by higher oscillations in atom distances.
-2.5	-5.0	-84.956	No		In this case the energy is high enough and the atoms are able to pass over the transition state energy maxima, however the vibrational energy of the HBHC system formed seems to be too high to form the molecule and the HC atom rebounds and the distance begins to decrease and so the HAHB is reformed but with considerably higher oscillations.
-2.5	-5.2	-83.416	Yes		The HC approaches the oscillating HAHB system, the HB atom rebounds between the two atoms, as it can be seen on the surface plot the system passes over the transition state maxima, back over to the other side and back again as this occurs. Finally the HBHC bond is formed with a high vibrationally energy

Jas213 (talk) 20:05, 28 May 2018 (BST) An overall concluding comment would have been expected. You could have also stated the kinetic energies in each case to support your point.

Transition State Theory

Question 5 State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition state theory is used to understand how elementary chemical reactions take place assuming a quasi-equilibirum between reactanting complexes and those at the transition state. The rate of reaction can be understood by inspecting the complexes at the maximum saddle point of the minimum energy pathway. The reactants are in equilibrium with the activated transition state complexes and can be converted to the products.

This theory is useful to theoretically understand a chemical reaction however it operates on a series of assumptions which limit the theory. Main Assumptions: Equilibrium is close in the systems Only one reaction pathway occurs There is negligable barrier recrossing

For instance the atoms are assumed to behave classically, ignoring tunelling. Tunneling would be more prominent in reactions with low activation barriers. Also the theory assumes that the saddle point with the lowest energy will be passed over to reach the products, however this is not the case when higher vibrational energies will be populated.

Clearly a key issue seen in the data obtained above is that there is considerable barrier recrossing. Therefore the transition state theory would fail in this case. The TST would assume that all collisions of an energy above the barrier of the transition state would result in a successful reaction. Clearly this is not the case and the experimental rate would be much lower than the TST would predict.

Jas213 (talk) 20:07, 28 May 2018 (BST) Good that you give the references, however you need to state them at the end of the specific sentences you have adapted from the references.

Exercise 2: H-H-F System

PES Inspection

Question 6. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

For the forward reaction of H₂ + F --> HF + H is exothermic, as shown in the surface plot below the energy of the reactants H₂ is higher than the energy of the product HF. As the energy absorbed in breaking the H-H bond in the first case is less than the energy released forming the H-F bond which means that in total energy is released which results in an exothermic reaction.

Surface Plot H2+F->HF+H	Surface Plot HF+H -> H2+F
	|

Bond	Strength (kJ/mol)
H-F	565
H-H	432

Determining Transition State

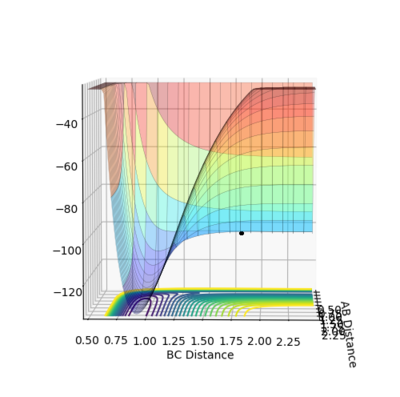
Question 7. Locate the approximate position of the transition state.

A = H_A B = H_B and C = F

Atoms	Internuclear distance
AB	0.74
BC	1.813

Surface Plot	Internuclear distance vs Time
	|

Jas213 (talk) 20:08, 28 May 2018 (BST) Not a single sentence on how you obtained the TS, no units, just throwing some plots and tables at me. Your distance vs. time plot shows wiggly lines, hence you haven't found the exact TS yet.

Calculating Activation Energy

Question 8. Report the activation energy for both reactions.

Initial Conditions

	Distance	Momentum
AB	0.74	0
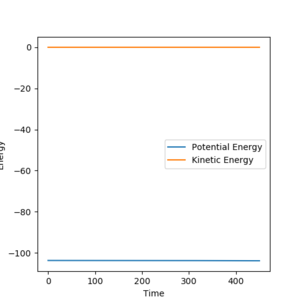
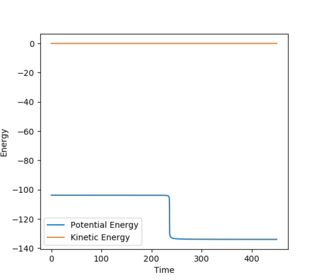
BC	1.8130/1.8135	0

BC= 1.8135	BC= 1.8135 Zoomed	BC= 1.8130
‎

Activation energy HF+H->H₂+F

	Energy (Kcal/mol)
Initial energy	-103.752
Final energy	-133.89
EA	30.138

Activation energy H₂+F->HF+H

	Energy (Kcal/mol)
Initial energy	-103.742
Final energy	-103.752
EA	0.01

Jas213 (talk) 20:11, 28 May 2018 (BST) Again not a single sentence? Did you use MEPs or Dynamic? to obtain these E vs. time plots? You could have provided them. Why do you have two BC distances, but only one AB distance? Some comments/ some discussion would have been nice. If you don't explain anything, how can I tell if you understood what you are doing.

Reaction Dynamics

F+ H₂

Initial Conditions

	Distance	Momentum
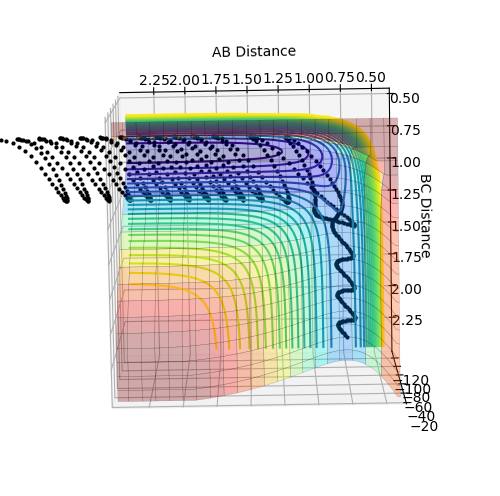
AB	0.74	0
BC	2.3	-2.7

Surface Plot	Internuclear momentum vs time

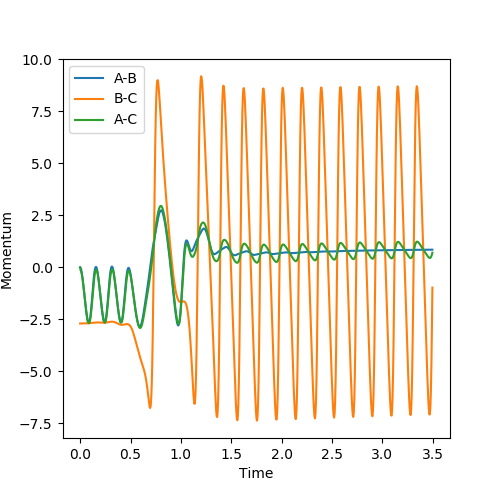
Energy
Kinetic	3.837
Potential	-103.886
Total	-100.049

Question 9. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

As energy is always conserved and can only be transformed from different forms to another. It can be seen from the animation that as the H-H (AB) bond is broken and the H-F (BC) bond is formed the vibrational energy (and so the kinetic energy) considerably increases for H-F. The internuclear momentum vs time graph demonstrates this, as the momentum is much higher for the H-F atom. As the vibrational energy begins to dampen the energy will be released as heat so experimentally an increase in temperature could confirm the reaction had occurred. Spectroscopy can be used to determine the vibrational energy of the bonds formed.

Atoms	Internuclear distance
AB	0.74
BC	2

pHH	pHF	Total Energy	Reactive?	Surface Plot	Explanation
-3	-0.5	-100.339	No		H2 approaches the fluorine atom slowly but when a collision is made the H rebounds straight back into the other H and they continue their path oscillating together in the opposite direction. This demonstrates recrossing, as the activation barrier is passed over but the products are not formed
3	-0.5	-93.254	No		This is similar to the previous case however the hydrogen rebounds twice into flourine but on the second rebounds remains returns back to oscillating with the original H atom
2	-0.5	-98.753	No		The HF molecule oscillates within the energy well at high vibrational energy after collision. The system remains in the products side after the reaction however the molecule remains in a high energetic state
1.5	-0.5	103.754	No		Similarly to the previous situation the fluorine slowly approaches the hydrogen molecule with a high vibrational energy and a high vibration energy molecule of HF is formed
0.1	-0.8	103.364	Yes		Despite having lower total energy than the previous cases the reaction goes to completion, increasing the momentum of the fluorine atom has a considerably more pronounced effect on the success of the reaction compared to any changes in the vibraitonal momentum of the oscillating hydrogen molecule.

Jas213 (talk) 20:17, 28 May 2018 (BST) Good effort showing all these examples, but any comments on what your result indicate?

HF+F

Atoms	Internuclear distance
AB	2
BC	0.74

pHH	pHF	Total Energy	Reactive?	Surface Plot	Explanation
-5	0.2	-103.364	No		Approaching H rebounds and reaction doesn't complete

A reactive pathway was found by trial and error around the reversed conditions from the reverse reaction.

Initial Conditions

	Distance	Momentum
AB	5.0	-1.5
BC	1.2	1.0

Polanyi's Empirical Rules

Question 10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that in reactions with an early transition state (most closely resembling the reactants) translational energy most effectively promotes a successful reaction. Conversely where the transition state is late (resembling products closely) vibrational energy, specifically of the reactants most effectively promotes a successful reaction.

This is demonstrated in the above, where the forward reaction H₂+F-> HF+H has an early transition state, as the activation barrier is so low and the transition state closely resembles the reactants. In this case a high translational energy of the incoming atom (fluorine) is more effective in resulting in a successful reaction and increasing the vibrational energy of the H₂ molecule has little impact. This is illustrated nicely in the table above.

In the reverse reaction HF + H -> H₂+F the transition state is late, as the activated complex much more closely resembles the product. A high vibrational energy of the HF molecule results in a successful reaction whereas increasing the translational energy of the approaching H atom has little impact.

Jas213 (talk) 20:19, 28 May 2018 (BST) Correct, you could have incorporated this discussion into the previous section and defined a reactive range of values, following the polanyi rules.