MRD:milandeleev

Exercise One

Question One

Q1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

A1. The total gradient of the PES should be zero at a minimum and transition state. To distinguish between these two, the second derivative must be taken (or the curvature analysed). If it is negative, this represents a local maximum (or transition state), and, if positive, represents a local minimum (intermediate/product/reactant).

Question Two

Q2. Report your best estimate of the transition state position and explain your reasoning, illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

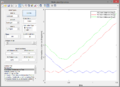
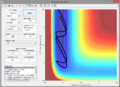
A2. To find the approximate position of the transition state, I plotted internuclear distance against time to find the point at which the nuclei were equidistant, since, in the transition state, $r_{1} = r_{2}$ . This was around 1Å, so I modified this internuclear distance until the line size on the surface plot was as small as possible, reaching a value of 0.907743Å (as seen below).

Question Three

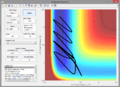
Q3. Comment on how the MEP and the trajectory you just calculated differ.

A3. The MEP just shows the path of lowest energy. It does not extend past the transition state which indicates that the reaction does not take place, but also does not indicate the graphical position of the reactants. The trajectory also shows that the reaction is unsuccessful, but shows where the reactants energetically are. See right for image.

Question Four

Q4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

A4.

p₁	p₂	Reactive?	Description
-1.25	-2.5	Reactive	The reactants have sufficient energy in the correct modes to reach the transition state and fall to the products.
-1.5	-2.0	Unreactive	The reactants have insufficient energy in the correct modes to reach the transition state, so do not form the products.
-1.5	-2.5	Reactive	The reactants have sufficient energy in the correct modes to reach the transition state and fall to the products.
-2.5	-5.0	Unreactive	The reactants have sufficient energy in the correct modes to reach the transition state. They pass the transition state, but still have much remaining energy, so revert back to the transition state and fall back to reactants.
-2.5	-5.2	Reactive	The reactants have sufficient energy in the correct modes to reach the transition state and fall to the products, which are high in vibrational energy.

Question Five

Q5. State the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

A5. Transition-state theory is based on the assumption that there is a potential energy surface that divides reactants from products, the maximum of which is known as the transition state, through which the system will only pass once before being stabilised. The assumptions that the Born-Oppenheimer separation holds (the reaction is electronically adiabatic) and that the reactants are equilibrated in a canonical or microcanonical sense are also vital for this theory.^[1]

↑ D.G Truhlar, B.C Garret and S.J Klippenstein (1996): Current Status of Transition-State Theory; in: Journal of Physical Chemistry 100, p12771.

Exercise Two

Question One

Q1. Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The strength of the H-H bond is 432 kJmol^-1, and the strength of the H-F bond is 565 kJmol^-1, making the reaction $\dot{F} + H_{2} \to H F + \dot{H}$ exothermic, due to the higher H-F bond strength.

Question Two

Q2. Locate the approximate position of the transition state.

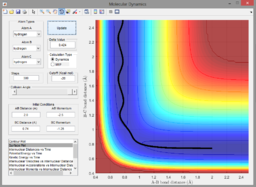
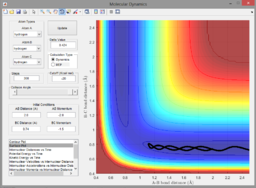
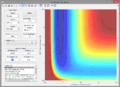
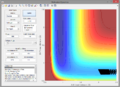
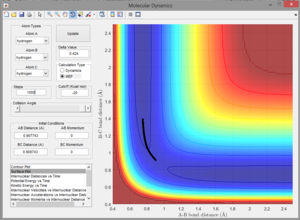
A2. Since the reaction is exothermic, invoking Hammond's postulate, the transition state is assumed to closely resemble the reactants. As a result, the H-H bond length ( $r_{B C}$ ) is kept constant to reduce the number of variables. The transition state was found at ca. 1.8175Å (see below).

Zoomed-out contour plot containing transition state
Zoomed-in contour plot containing transition state

Question Three

Q3. Report the activation energy for both reactions.

A3.

Question Four

Q4. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

A4. The image adjacent shows the large, oscillating fluorine-hydrogen internuclear momentum generated after the reaction. This indicates that the majority of the reaction energy is released into vibrational energy in the hydrogen fluoride molecule, stretching and compressing the H-F bond. This could be experimentally confirmed by monitoring the IR radiation emitted by the reaction: there should be a single, very strong peak when the reaction is complete, which indicates the release of heat energy of a single wavelength due to the oscillation of the H-F bond.

Question Five

Q5. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

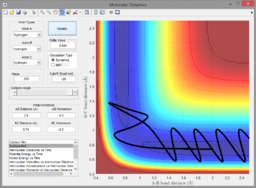
A5. Using the values in figure 1 ( $r_{A B} = 2.30 Å$ , $r_{B C} = 0.74 Å$ and $p_{A B} = - 0.5$ , the value of $p_{B C}$ was varied between 3 and -3. All values put a large amount of vibrational energy into the H-H system, and none resulted in a successful reaction. This is because, according to Polanyi's empirical rules, vibrational energy is more efficient in promoting late-barrier reactions than translational energy. The reaction $\dot{F} + H_{2} \to H F + \dot{H}$ is exothermic, meaning, that if Hammond's Postulate is invoked, it reaches its transition state early so is an early-barrier reaction. This means that the vibrational energy in the H₂ molecule is not effective at promoting the reaction.

However, setting this value constant at 0.1 and slightly increasing the value of p_AB to -0.8 allowed the reaction to proceed closer to products, albeit in a highly vibrationally energetic manner (see figure 2). This shows that the higher translational energy of the free fluorine atom was better at promoting the reaction than the large vibrational energy of H₂ in the previous part.

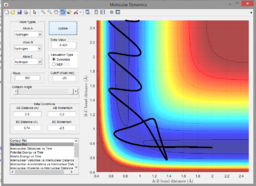
Considering the endothermic reaction, one would expect the opposite to be true, since the reaction $\dot{H} + H F \to H_{2} + \dot{F}$ is endothermic and therefore early-barrier. This means that the vibrationally excited HF molecule should be more efficient at promoting reaction than the translationally excited H atom. Indeed, this was found to be true, as seen in figures 3 and 4. In figure 3, a weakly vibrationally excited HF molecule does not even reach the transition state. In figure 4, the vibrationally excited HF molecule reaches and passes it!

Figure 1
Figure 2
Figure 3
Figure 4

[Transition-State_Theory-1] D.G Truhlar, B.C Garret and S.J Klippenstein (1996): Current Status of Transition-State Theory; in: Journal of Physical Chemistry 100, p12771.

[1]