MRD:mhz15

Introduction

This is the page created by Hafiz Zainal to report the results of his Molecular Reaction Dynamics simulation using MATLAB.

H + H₂ System

The reaction between an H₂ molecule and an H atom is discussed below through the use of plots obtained from MATLAB.

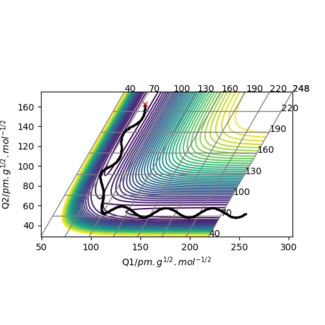
Surface plot

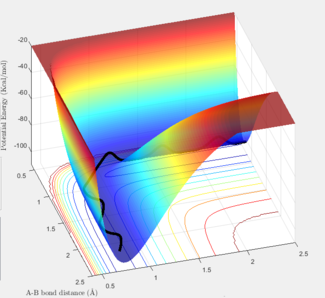
The surface plot shows the variation of potential energy of an H atom in collision with an H₂ molecule.

The blue-red spectrum corresponds to the potential energy range with blue being the minimum and red the maximum.

The black wavy line illustrates the path of H₂ along the minimum vibrational energy of the diatomic molecule.

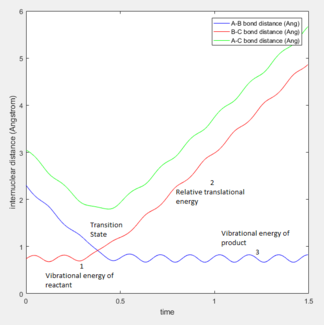
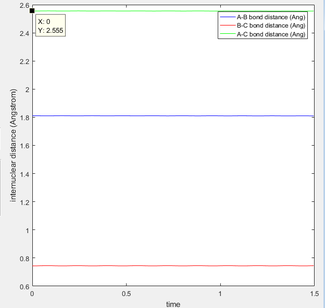
Interpreting the distance vs time plot

At the beginning of the sequence, r₂, corresponding to the internuclear distance of H_A-H_B, decreases from ~2.3 Å to a minimum ~0.6 Å where it oscillates relative to the middle H_B atom.

r₁, corresponding to the internuclear distance of H_B-H_C, increases as H_A approaches H_B. Eventually H_C breaks away from the attraction of H_B and moves away to a maximum r₁.

The sequence shown illustrates the transition state where r₁ is equal to r₂ at about 0.9 Å.

The animation still mentioned above ties in with the discussion of the H - H₂ reaction dynamics in terms of internuclear distance.

The H atoms in molecule H_C-H_B (shown in red) maintain their oscillation while H_A moves closer towards H_B, illustrated in blue.

The potential energy of H_A, relative to the two other H atoms, increases as it approaches H_B up to a point - the transition state - where the the internuclear distance of H_A and H_B equals that of H_B and H_C.

As has been mentioned above, H_A oscillates around H_B, shown in blue, past the transition state, and H_C gains kinetic energy as it moves away and loses potential energy.

The plot illustrates the trajectory of the transition state at r₁ = r₂ = r_ts when r_ts is approximated to 0.9078 Å and p₁ = p₂ = 0.

The gradient of the trajectory is zero. The internuclear distance between H_A and H_B is around 1.8 Å which agrees with the approximated value at which the transition state forms, as shown in the above still of the reaction animation.

Reaction path

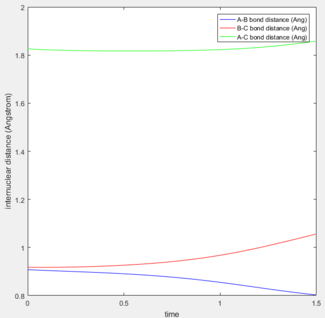The above internuclear distance vs time plots show the path of the reaction starting from the transition state, when r₂ = r_ts = 0.9078 Å and r₁ = r_ts + 0.01 and the momenta p₁ and p₂ set to 0.

The reaction path in mep refers to the trajectory along the minimum energy pathway.

Reactive and unreactive trajectories

Trajectories with the following momenta combination were run while p₁ = p₂ = 0:

p₁	p₂	Reactivity
-1.25	-2.5	Reactive
-1.5	-2.0	Unreactive
-1.5	-2.5	Unreactive
-2.5	-5.0	Unreactive
-2.5	-5.2	Reactive

Surface plot of the trajectory with conditions p₁ = -1.25, p₂ = -2.5, and p₁ = p₂ = 0.

The reaction pathway crosses the route along the floor of the potential valley, which is the path that requires the H₂ and H molecules to have relatively small initial kinetic energies.

This pathway takes the reactant molecules to regions of least potential energy, as r₁ increases as the H_A atom approaches H_B.

The trajectory continues its path as H_C moves away and the new H_A-H_B bond forms.

Surface plot of the trajectory with conditions p₁ = -1.50, p₂ = -2.0, and p₁ = p₂ = 0.

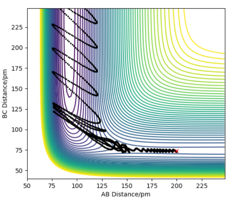
The reaction pathway does not go along the floor of the potential valley - it stops at the point where the H₂ molecule possesses equilibrium bond length.

The H_A-H_B bond does not form.

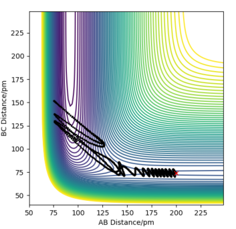
Surface plot of the trajectory with conditions p₁ = -1.50, p₂ = -2.5, and p₁ = p₂ = 0.

The reaction pathway moves along the floor of the potential valley.

This pathway takes the reactant molecules to regions of least potential energy, as r₁ increases as the H_A atom approaches H_B.

The trajectory continues its path as H_C moves away and the new H_A-H_B bond forms.

Surface plot of the trajectory with conditions p₁ = -2.50, p₂ = -5.0, and p₁ = p₂ = 0.

The trajectory moves along a different path that does not cross the saddle point - a path that makes the reaction feasible if the molecules have enough initial kinetic energy.

H_A forms a bond with H_B as the trajectory crosses past the saddle point but it moves back towards the initial path.

The H_A-H_B bond breaks again.

Surface plot of the trajectory with conditions p₁ = -2.50, p₂ = -5.2, and p₁ = p₂ = 0.

The trajectory moves along a different path and does not cross the saddle point.

This path requires higher initial kinetic energy. The trajectory continues along the path down the floor of the other valley, after the formation of the new H_A-H_B bond.

F - H - H System

Classifying endothermic and exothermic reactions

In the H + HF reaction, the bond breaking is between the hydrogen and fluorine atoms. The H-F bond is relatively stronger due to a large difference of electronegativities between that of hyrodgen and fluorine atoms. Fluorine attracts the hydrogen atom stronger. Thus a large amount of energy is required to break the bond, and this makes the H + HF reaction endothermic.

In the F + H₂ reaction, the bond breaking is between the two hydrogen atoms. The H-H bond is relatively weaker due to an approximately zero difference of electronegativities between the two atoms. A smaller amount of energy is required to break the H-H bond, thus the reaction is exothermic.

The transition state

The plot on the center illustrates the transition state of an F - H - H reaction, and it occurs when r_FH = 1.811 Å and r_HH = 0.744 Å, and the initial momenta set to 0.

Activation energies

In the F + H₂ reaction, the transition state resembles the reactants more due to its exothermic nature. Thus the difference between the highest point of kinetic energy and the lowest point on the side of the reactants is equal to the activation energy. The activation energy is found to be 22.574 kcal/mol.

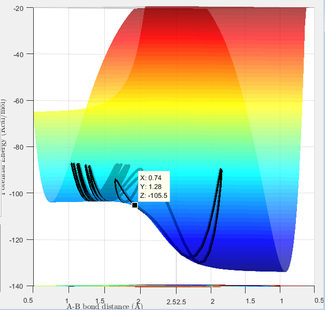
In the H + HF reaction, the transition state resembles the products more due to its endothermic nature. Thus the difference between the highest point of kinetic energy and the lowest point on the side of the products is equal to the activation energy. The activation energy was found to be 28 kcal/mol.

Reaction dynamics

F + H₂ reaction

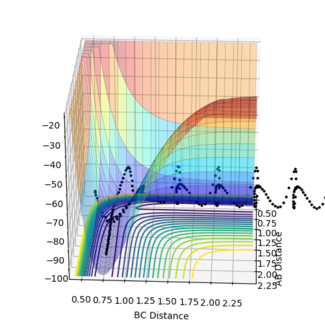
The reactive trajectory was found using initial conditions of r_FH = 1.48 Å and r_HH = 0.74 Å, while momenta were set to 0.

As F approaches H_B and forms a bond with the atom, its potential energy increases, and H_A, the leaving atom, loses potential energy and gains kinetic energy.

Testing different p_HH and p_FH values

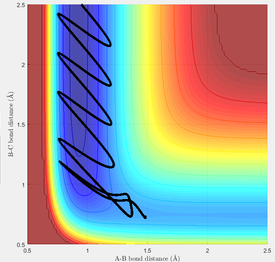A range of values for p_HH from -3.0 to 3.0 was explored with the trajectory starting at the bottom of the well. The conditions used were r_FH = 1.48 Å, r_HH = 0.74 Å and p_FH = -0.5. In all of the reactions tested, the products are converted back to the reactants. This is due to there being an excessive amount of energy into the system.

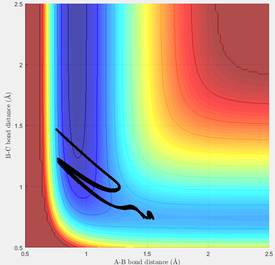
The trajectory when p_FH = -0.8 and p_HH = 0.1.

Using the same initial conditions as above, the reaction was tested with p_FH = -0.8 and p_HH = 0.1, reducing the overall energy of the system.

The trajectory leads to a reaction but H_C and F remain in oscillation relative to the central H_B.

H + HF reaction

The trajectory when r_HF = 1.811 Å, r_HH = 0.74 Å and p_HF = -0.2, p_HH = -2.2.

The value of p_HH was set to a high value above the activation energy.

The trajectory with the same conditions as above except p_HF = -0.1 and p_HH = -1.2.

The trajectory leads to a reaction when p_HF = -0.1 and p_HH = -1.2.