MRD:mhmh
Exercise 1: H + H2 system
Dynamics from the Transition State Region
The mathematics of potential energy surfaces (as a function of inter-nuclear separation) indicate many features of molecular collisions, principally being used to determine both the thermodynamic and kinetic feasibility of a given collision (of reactant molecules) resulting in the formation of product molecules. [1]</references>
of The transition structure corresponds to a maximum on the minimum energy path, which is a saddle point in the potential energy surface. As with the minimum in the potential energy surface, the total gradient of the potential energy surface has a value of zero at both of these stationery points.
Distinction Between Maxima and Minima
A true minimum and a saddle point can be distinguished by using the 'Two-Variable Second Derivative Test'.
Therefore, we must find the value of the equation:
at each point.
The minimum in the potential energy surface will have: a as a positive value, The saddle point in the potential energy surface (the transition structure) will have: a as a negative value.
Locating the Transition State
The best estimate for the transition state is: rts = 0.90775 A
This is because this is the value of the equidistant A-B and B-C internuclear distances at which there is no oscillation in either bond length, so must correspond to the transition state sine.... FINISH!!
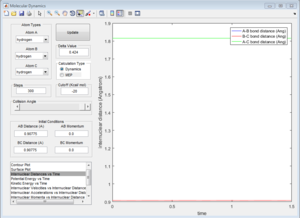
The value of r1 (B-C distance) differs in the 'Dynamics' version and the MEP version. Using the Dynamics run (snce this is more representative of the true structure), with 300 steps:
At time, t = 2.00s:
r1 (B-C distance) = 0.7553 A r2 (A-B distance) = 7.155 A
p1 = + 2.481 p2 = + 1.122
With the offset (from the transition strucutre) changed to the opposite direction, the atoms revert back to the original reactant molecule, BC and atom A, rather than giving the product AB and dissociated atom C.
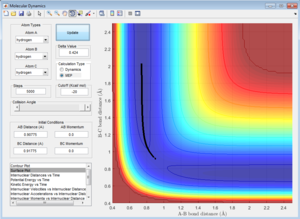
Minimum Energy Path (MEP) vs. Trajectory
Both the minimum energy path (mep)and trajectory shows the variation in A-B bond length (r2) as a function of increasing B-C bond length (r2), starting from a position on the potential energy surface which is slightly offset from the transition state, i.e. observing how the point 'rolls' across the PES in the direction of increasing r2.
The MES, however, has fewer degrees of freedom - the potential energy is held constant, at the minimum value (and therefore kinetic energy and other degrees of freedom are also fixed). Therefore, the mes can be considered as a pseudo-two variable system, in which the only variables free to change are A-B (r2) bond length, and B-C bond length (r1), with fixed potential energy (corresponding to the minimum).
However, the dynamic trajectory does not have such limitations, and therefoer shows a system which is subject to more degrees of freedom. Therefore, potential energy is not fixed at the absolute minimum value, and so the line observed in the Internuclear Distances vs. Time plot (Figure .....) is not perfectly straight - it fluctuates as the potential energy interconverts between kinetic energy, around the minimum value(in potential energy), but not fixed at this value.
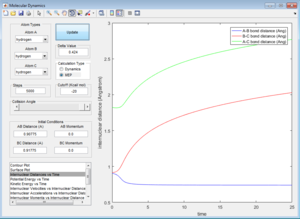

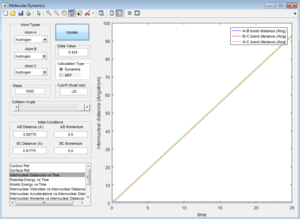
When the initiaal positions correspond to the final positions of the trajectory, and the final momenta have their signs reversed, we just observe the final AB molecule vibrating about its equilbirum bond length, with the C atom dissociated.
Reactive Trajectories
| Initial Conditions | p1 | p2 | Reactive or Unreactive Trajectory? |
|---|---|---|---|
| 1 | -1.25 | -2.5 | Reactive |
| 2 | -1.5 | -2.0 | Unreactive |
| 3 | -1.5 | -2.5 | Reactive |
| 4 | -2.5 | -5.0 | Unreactive |
| 5 | -2.5 | -5.2 | Reactive |
Initial Conditions 1
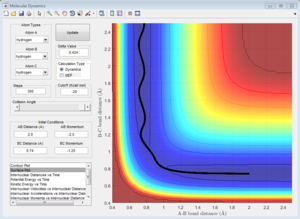
Along the reactive trajectory, the AB internuclear distance decreases as the A atom approaches the BC molecule. At the transition state, the BC bond is breaking as the AC bond is forming, and the momentum p2 (along the AB internuclear distance) is so great that it can overcome the activation barrier, and the B-C bond breaks with C dissociating, and its momentum increasing in magnitude as it dissociates away from the newly-formed AB molecule. The A-B bond thus oscillates about the equilibirum bond length, with the internuclear momentum ocillating as the total energy of the A-B bond interconverts between potential and kinetic energy.
Initial Conditions 2
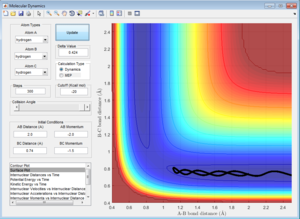
Atom A approaches moleculke BC (which is oscillating about the equilbirium bond length). However, the momentum along A-B (p2) is so low that A has insufficient kintetic energy to to overcome the activation barrier, and therefore approaches B, with the magnitude of p2 decreasing to 0 at a closest distance of 1.116. At this point, A rebounds, and the momentum increases in the opposite direction as A dissociates away from BC.
Initial Conditions 3
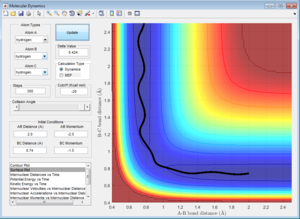
A approaches the molecule BC with a momentum (p2) sufficient to overcime thee energy barrier for A-B bond formation. The momentum along the B-C bond (p1) is greater than in the Initial Conditions 1, and so the dissociation of C is more easil;y achieved (i.e. the B-C bond breaks more quickly) because C has a greater kinetic ernergy to begin with, soi starts at a point which is closer to the transition state, so effectively the activation barrier for reaction is larger.
Initial Conditions 4
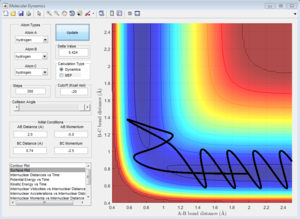
Initial Conditions 5
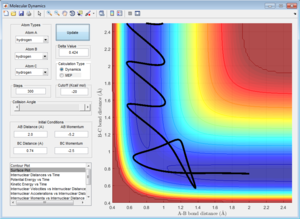
Transition State Theory
The transition state is a saddle point. At this precise point on the potential eenrgy sufacre, the reacting atoms must have a very specific arrangment (i.e.e all bond lengths must have a very specific value).1 Therefore, the probability of a given trajectory (which results in successful reaction), reaching this precise point is very low. Since we know tht these reactions are reactive, they must have an energy which either equals or exceeds the activation energy1 (which is the potential energy corresponding toi the saddle poiint). Therefore, many reactive trajectories do not actually pass exactly through the transition state geometry, and so therefpore, the system must have an overall energy which exceeds the potential energy at the saddle point (transition state structure).1 Hence, for a given reactive trajecotry (which does not pass eactly through the transition strucuture) must have a maximum experiemntal potentiual energy (the activation energy) greater than the energy at the saddle point.1
Therefore, transition state thepory predicts that it is very likely that experimental reaction rates will be slower than the calculated values, due to the hiugher experiemntal activation enrgy. this is expressed by Arrhenius' law : k=Ae-Ea/RT 1.
Exercise 1: F + H2 system
The H2 + F reaction is exothermic. This can be easily determined by observation of the surface plot : as A-B internuclear separation decreases from an effectively infinite separation (as F atom approaches H2 molecule), the potential energy decreases to a minimum. Exothermic reactions are defined as reactions in which products have a lower total potential energy than reactants, so the lower potential energy at a small B-C internuclear separation, and large A-B (i.e. when the H-F bond has formed and H-H has broken) indicates that the formation of HF and dissocaiton of H2 is an exothermic process. This is shown in Figure ...

Therefore, the reverse reaction (HF dissociating and H2 reforming) must by definition be an endothermic (i.e. enthalpically unfavourable) process, as shown in Figure ....

This proves that the HF bond must be stonger (have a more negative enthalpy of formation) than the H2 bond - since the H2 and F sytem which forms a HF bond at the expense of a H2 bond has a negative (exothermic0 reaction enthalpy.
This is proven in the literature: Enthalpy of formation of HF(g) = Enthalpy of formation of H2 =
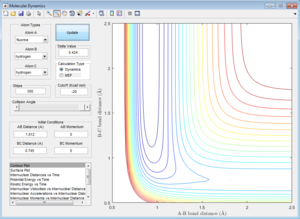
Loacting the Transition State
The transtion state can be approximated (to 3 decimal places), to:
A-B (H-F internuclear separation): 1.812 A B-C (H-H internuclear separation): 0.745 A
This can be shown in Figure ...
Activation Energy
(To two decimal places)
Absoulte energy of the transition state:-103.75 kcalmol-1
Absolute energy of H2 and F: -104.02 kcalmol-1
Absolute energy of HF and H: -134.01 kcalmol-1
Activation energy to form H2 and F: -103.75 - (-104.02) = 0.27 kcalmol-1
Activation energy to form HF and H: -103.75 - (-134.01) = 30.26 kcalmol-1
Mechanism for Release of Reaction Energy
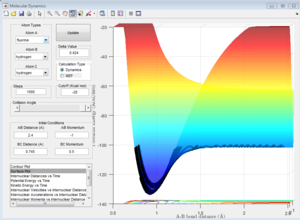
As shown in Figure..., the vibrational energy in the reactants is smaller than the vibrational energy in the products (since the amplitude of the ocsillaions in the corresponding directions is much larger in the proucts (in the A-B bond, i.e. H-F).
The translational kinetic energy is approxiamtely equal in the reactant and product staetes (as the period of the oscillations is approximately thee same).
Therefore, the total kinetic energy (vibrational plus translational, neglecting rotational, as there is zero rotation in a diatomic molecule) is greater in the products (HF and H). However, due to the Conservation of Energy, the total energy of the system (potential energy plus kinetic energy) must remain constant.
Therefore, the potential energy of the product state must be lower than reactants - which we know is true as we have already found the H2 + F -- HF reaction to be exothermic. This is shown in the surface plot, Figure...
This could be proven by several different experimental methods, including infrared spectroscopy and calorimety.
Infrared Spectroscopy
In the reactants, the vibrational kinetic energy is lower. Therefore, the reactant and product systems could each be monitored experiemnetally by recording an IR spectrum for each system. For the reactant system, the intenisty of absorption of the H-H bond would be much lower thann the intensity of the absorption peak corresponding to the H-F bond.
Calorimetry
Conversely, due to the higher total kinetic energy of the product system, the products are hotter than reactants - the exothermic nature of the reaction means that temperature of the systme increases as heat energy is released. Therefore, calorimetry, which is a technique used to measure the change in heat energy of a reaction, could be used to monitor the given reaction.
Polanyi Rules
The Polyani rules state that late transition states (those corresponding to endothermic reactins, according to Hammond's postulate) are enhanced by a greater vibrational energy, whereas early transition states (corresponding to exothermic reactions) are favoured by a higher translational kinetic energy (so lower vibrational kinetic energy).2
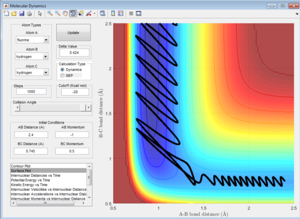
Therefore, the case study of the HF plus H reaction with different pHH and PHF momenta values allows a visual example of these rules. This reaction is an endothermic reaction, so has a late transition state, by Hammond's postulate.1 Therefore, according to the Polyani rules, the forwards reaction will be promoted by a higher vibrational kinetic energy than translational k8inetic energy in the reactajnts.
This is shown as such:
For a high initial BC momentum (pBC = 9.26) (corresponding to high H-H vibrational energy), with a low initial translational kinetic energy (pAB = -0.9), the forwards reaction is kinetically favoured, as shown by the existence of a reactive pathway in Figure ....
References [1] </references>
1 Atkins
2Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction
Zhaojun Zhang, Yong Zhou, and Dong H. Zhang* , State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, Liaoning, China
