MRD:mea15
Molecular reaction dynamics
Exercise 1 H2+H system
At a minimum the potential energy surface will have a gradient of 0 as both potential energy derivatives for each direction will be minima.
At a transition state structure the potential energy surface will have a gradient of 0 as it is a maximum of the minimum energy pathway, it is a saddle point.
When the curvature of the potential energy surface is considered for the minima the curvature will be larger than 0 as around the minima the potential energy will be larger than the minima itself so the surface will curve upwards.
At the transition state a saddle point will occur where the surface curves up in some directions and down in other directions.The saddle point can be identified by taking the determinant of the hessian matrix which is made up of the partial derivatives fxx fxy fyx and fyy, if the determiant is smaller than 0 then the saddle point is found.
Finding the transition state
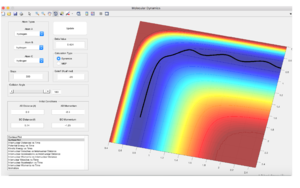
The best estimate of the transition state position is 0.90775 angstroms for both distances. This is backed up by the figure below as there is almost no oscillatory motion thus showing that the transition state position has been found as if placed on the transition state there should be no movement due to the transition state being a minima when the distances are equal to each other, any oscillations would show the minima has not been found.
Trajectories from r1 = rts+δ, r2 = rts
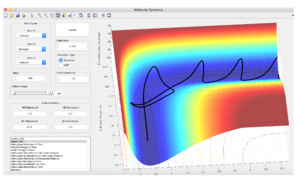
The mep and trajectory differ by the mep has no motion representing the molecules oscillating. It just follows the lowest energy path while the dynamics trajectory does not follow the lowest energy path as in the dynamics simulation the molecules oscillate and thus the trajectory follows a wave like motion through the valley instead of a straight one due to energy changes between vibrational and translational modes taking place. In the mep there is no such energy change
At large times, r2 increases steadily to 372.6 angstroms at a large time while r1 oscillates at 0.748 after initially decreasing slightly from the rts value. p1 oscillates around an average value of 1.248 while p2 increases and then remains steady at 2.481.
initial conditions r1 = rts and r2 = rts+0.01
By changing and using these new initial conditions would cause the trajectory to follow the valley that corresponds to r2 being constant instead of r1 being constant as the initial position is on the the other side of the transition state in comparison to the original initial conditions. The internuclear distances r2 and r1 will swap their values and behaviour, the same also applies for the internuclear momenta values.
The trajectory reaches the initial conditions used above and then goes back to the position at which the dynamics run begun at when the initial positions described above correspond to the final position and the momenta have their signs reversed.
Reactive and unreactive trajectories
| P1 | P2 | Reactive or unreactive | Screenshot | Description |
|---|---|---|---|---|
| -1.25 | -2.5 | Reactive |  |
The trajectory reaches the transition state, goes over the transition state and then oscillates through the constant AB bond distance valley. This corresponds to molecule A-B being formed from A hitting molecule B-C, the momentum and energy is sufficient to go over the activation state. |
| -1.5 | -2.0 | Unreactive |  |
The trajectory almost reaches the transition state and the goes back along its original path, this is due to the momentum values not being large enough so there is not enough energy to overcome the barrier of the transition state. |
| -1.5 | -2.5 | Reactive |  |
The trajectory reaches the transition state, goes over the transition state and then oscillates through the constant AB bond distance valley. This corresponds to molecule A-B being formed from A hitting molecule B-C, the momentum and energy is sufficient to go over the activation state even though the P1 momentum is close to being too large for the reaction not to occur. |
| -2.5 | -5.0 | Unreactive |  |
The trajectory reaches the transition state and then recrosses the transition state, this is a case of barrier recrossing due to the ratio of translational to vibrational energies being incoorect |
| -2.5 | -5.2 | Reactive |  |
The trajectory reaches the transition state and then crosses it a couple of times before going into the product valley. The ratio of the energies of the atoms changes each time the barrier is crossed until the correct ratio is reached and trajectory then moves towards the products. |
The main assumptions of Transition State Theory and how it compares to experimental results
Transition state theory assumes the system is close to equilibrium, there is only one reaction pathway which the reaction proceeds down and there is very little recrossing of the barrier, transition state theory also assumes that the reaction follows the Boltzmann distribution[1]. Transition state theory breaks down at high temperatures as these conditions are not fulfilled, this can be seen in the pictures above when there is significant recrossing due to large translational energies being present.
Experimental values will be larger as transition state theory neglects the effect of tunneling which can occur in this situation due to the very small masses used in this experiment.[2]
Exercise 2 F - H - H system
F+H2 is exothermic while H+ HF is endothermic. The first reaction is endothermic as the potential energy surface drops after the reaction showing the products have less energy than the reactants. The inverse occurs for the the H+HF reaction. This relates to the bond strength by H-F having a larger bond strength than H-H and therefore being lower in energy, this means when the bond is formed energy will be released and so the reaction is exothermic as the energy released from the formation of the H-F bond is much larger than the energy required to break the H-H bond.
Locating the approximate position of the transition state
AB=1.8102, BC=0.746 after an 1000 steps dynamics run, this transition state closely resembles H2 + F instead of HF and H as predicted by Hammond's postulates which states that an exothermic reaction will have a transition state much more similar to the reactants than the products.
Reporting the activation energy for both reactions
The activation energy for the F+H2 reaction is 0.2 kcal mol-1 while the opposite reaction has an activation energy of 30.3 kcal mol-1. This was calculated by finding the energy at the transition state and then comparing it to the lowest energy at the initial positions for each reaction.
Identifying a set of initial conditions that results in a reactive trajectory
When distances AB and BC are set to 2.5 and 0.74 respectively it is found that when the momentum between AB is set to -2, BC has a momentum value of between -0.61 and 1.66 for the reaction to occur. The reaction energy is released by converting translational energy into vibrational energy, the vibrational energy then causes the bonds to be broken, thus releasing the energy by decaying down excited vibrational states. The energy released could be determined by looking at a vibrational spectra as the spectra would show a different vibration that corresponds to a different energy when the energy is transferred.
Setting up a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and exploring several values of pHH in the range -3 to 3
By exploring this range it is found that values under 2.2 in the positive momentum direction and -2.75 in the negative momentum direction do not go over the transition state, this is due to not enough vibrational energy being in the system causing the bonds to break. Meanwhile at values above 3 in both directions there is a significant amount of barrier recrossing resulting in unreactive trajectories due to the incorrect ratios of vibrational and translational energies being present in the system.
For the same initial position the momentum was increased to pFH = -0.8, and the overall energy of the system was reduced by reducing the momentum to pHH = 0.1.The reaction occurs after significant amounts of barrier crossing takes place. This is due to the energy being transferred between vibrational and translational modes until the correct ratio is reached and the barrier is crossed successfully. This shows that for this reaction the amount of translational energy is much more important than the vibrational energy in the system.
The reverse reaction, H + HF.
A reactive trajectory occurs at AB=0.74 angstroms, BC=2.5 angstroms with the momenta being AB=0.5 and BC being -0.45. This reaction depends much more on the amount of vibrational energy compared to the amount of translational energy of the system. This is the inverse of the reaction occurring in the opposite direction.
Discussing how the distribution of energy between different modes (translation and vibration) affects the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules state that a early transition state is climbed more easily with translational energy while a late transition state is climbed more easily with vibrational energy[3]. This means that the reaction will occur quicker if the energy is distributed in the correct modes, an early transition state requires the distribution of energy to favour the translational modes while a late transition state will require the distribution of energy to favour the vibrational modes in order for the efficiency of the reaction to increase.