MRD:mb7418
EXERCISE 1: H + H2 system
To me it looks like you understood what you are doing, although you have problems expressing yourself in a clear way sometimes. for example, "The transition state is the minimum energy required for the reactants to convert into the products" is wrong - that would be the activation energy, not the transition state. (What is the difference? look at the absolute energies...) Fdp18 (talk) 08:50, 30 May 2020 (BST)
Dynamics from the transition state region
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface? This text is repeated below which makes this section difficult to read. Mak214 (talk) 18:03, 29 May 2020 (BST)
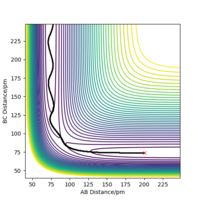
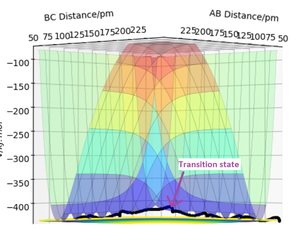
Potential energy surface diagrams show the potential energy the system has according to the coordinates of the atoms in the system.[1] Figure 1 shows a potential energy surface diagram representing the reaction, equation 1: A + BC → AB + C.
| r / ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r2=r(AB) | 230 | -5.2 |
| r1=r(BC) | 74 | 0 |
In this case r(1)=r(BC) and r(2)=r(AB). BC is a hydrogen molecule consisting of two hydrogen atoms, B and C. Atom A is a hydrogen atom which has energy equal to or more than the activation energy, thus reaching the transition state. The transition state structure consists of atom A forming a bond with molecule BC while the BC bond is slightly dissociating. After the transition state, the bond between AB would form making a new molecule and the BC bond would be fully dissociated.
- Q1. On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
In a potential energy surface diagram, the transition state is mathematically defined as the first-order saddle point[2]:
∂V(r1)/∂(r1)=0 and ∂V(r2)/∂r2=0
∂2V(r)/∂(r1)2 > 0 and ∂2V(r)/∂(r2)2 < 0
[∂2V(r)/∂(r1)2]*[ ∂2V(r)/∂(r2)2] - [ ∂2V/∂(r1)(r2)]2 < 0
Hessian matrix is shown in Table 2, resulting in DET = -0.999698 < 0
| f(x) | f(y) | |
|---|---|---|
| f(x) | +0.707 | -0.707 |
| f(y) | -0.707 | -0.707 |
In Figure 1, the black wavy lines shows that the molecule is vibrating. This is the minimum energy path required for the reactants to react and turn into the products via the transition state.[3] This suggests that the transition state is the peak in the minimum energy path. The transition state is the minimum energy required for the reactants to convert into the products. Hence once the transition state is reached, if the reaction was successful the products would be formed. Figure 1 shows the location of the transition state in the potential energy diagram.
The transition state can be distinguished from a local minimum of the potential energy surface because it is on the diagonal axis. Because it is also a maximum (minimum AND maximum in orthogonal directions.. i.e a saddle point) therefore distinguishable from a local minimum. Mak214 (talk) 18:03, 29 May 2020 (BST)
It is the saddle point.This is when everything in the system is stationary when there is no momentum.
Locating the transition state r1=r2
- Q2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
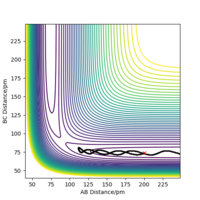
When the transition state is formed, due to all the atoms being hydrogen, this suggest that the transition state is symmetrical. This means that the bond distance between A and B is the same as the bond distance of B and C. This can be used to locate the transition state when the momentum is 0. Table 3 shows an estimate of the transition state position (rts).
| r / ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r2=r(AB) | 90.75 | 0 |
| r1=r(BC) | 90.75 | 0 |
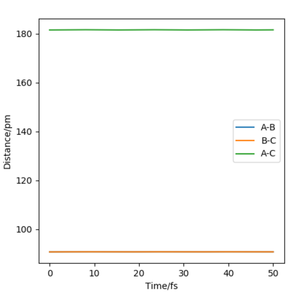
Figure 2 shows an Intermolecular distance vs time graph resulted from the initial conditions from Table 2. The line is flat, this suggest that everything in the system is stationary. Whereas, if it wasn't the transition state, in the intermolecular distance vs time graph you'd see oscillations representing the vibrational movements. The more oscillations would indicate the more vibrational movements. Hence the transition state is a flat line as there isn't any. OK. Mak214 (talk) 18:33, 29 May 2020 (BST)
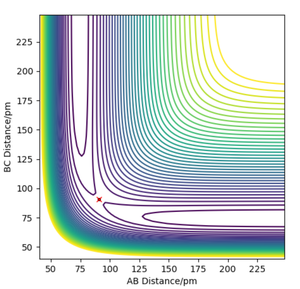
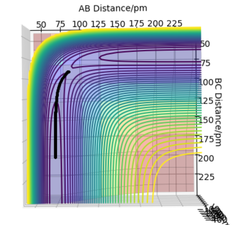
The contour plot shown in Figure 3 shows the transition state as a red cross. This is the saddle point of the potential surface. Whenever r1 and r2 are the same, the point would be anywhere across the diagonal axis. This contour plot helped estimate the transition state position as the trajectory shows that the AB and BC bond lengths are the same. This is the point at which reactants have to overcome to react into the products.
The minimum energy path can differ depending on the relative momentum of the atoms/molecules and their vibrational excitation energy. The transition state of the reaction won't change its position. The reactants require sufficient translational kinetic energy and vibrational energy to overcome the transition state (saddle point) in order to react and turn into the products.
Trajectories from r1 = rts+δ, r2 = rts
- Q3. Comment on how the mep and the trajectory you just calculated differ. r1 = rts+1 pm, r2 = rts and the momenta p1 = p2 = 0 g.mol-1.pm.fs-1
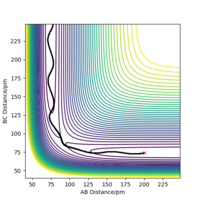
The trajectory of the minimum energy path can be visualised slightly near the transition state, this is when atom A is approaching molecule BC to form a bond with it, A + BC.
| r /ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r2=r(AB) | 90.75 | 0 |
| r1=r(BC) | 91.75 | 0 |
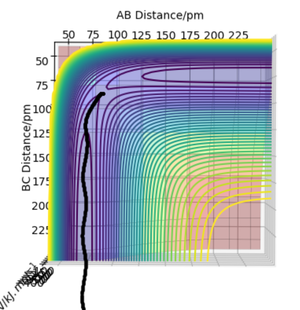
The initial conditions shown in Table 4 gives the potential energy diagram in Figure 4 and 5 when the calculation type is MEP. The minimum energy path shown by the black line isn't wavy.
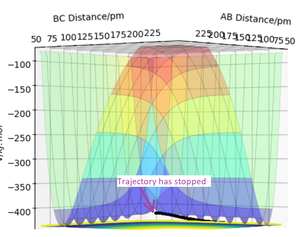
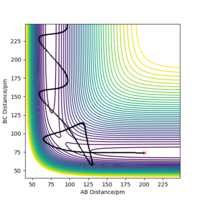
However, when the same initial conditions are applied when the calculation type is Dynamic, the minimum energy path is wavy shown in Figure 6. This shows that the MEP calculation gives a different result of the reaction trajectory. The molecule is constantly moving at a velocity since there is no external force acting upon the reactants. This is called inertia motion.[4] Whereas the potential energy diagram produced from the Dynamics calculation takes into account the reactants inertia by representing the pathway as non-linear. Additionally, the MEP calculation diagram has a smaller trajectory than the Dynamics calculation.The reason for this is beacause the MEP calculation sets the momentum to zero at every step whereas the dynamic calculation the momenta is developed classically[5]. The MEP calculation only takes the gradient into account. The amount of steps there are corresponds to the number of times it is calculating what the gradient is at that point. The only thing relative to the MEP calculation is the gradient. Whereas with dynamics, it takes into account how long it takes for the gradient to change. The momentum (velocity) is changing each time instead of setting it to zero every step. Hence it's longer as after the products are formed, they are still have motion such as vibrational and kinetic. Yes. This does show an understanding of MEP vs Dynamics. Just to clarify - the amount of steps is the number of times the system moves during the simulation - this was a bit confused in your response. Mak214 (talk) 18:36, 29 May 2020 (BST)
Reactive and unreactive trajectories
Interpreting trajectories
- Q4. For the initial positions r1 = 74 pm and r2 = 200 pm, run trajectories with the following momenta combination and complete the table.
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Reactive | The starting point (represented by the red cross) starts at 200 pm between atoms A and B. Then the distance AB decreases. Atoms A and B are approaching each other and once it reaches the transition state, the AB distance and BC distance are the same and all the atoms are stationary. Then the AB bond is formed and atom C repels from atom B. The molecule AB is constantly vibrating. This could suggest that some translational kinetic energy got converted into vibrational energy after the transition state. Hence after the trajectory has oscillations after it passes the transition state. |  |
| -3.1 | -4.1 | -420.077 | Unreactive | The trajectory has some oscillations, showing that the reactants are constantly vibrating. Hence it has vibrational energy. However, it doesn't go over the transition state so it doesn't react into the products. This suggests that the reactants approach each other but then they repel. While they do that they oscillate as they get closer. It ends up with a high AB distance (essentially the starting point of the reaction), this shows that the reactants haven't reacted due to the AB molecule not forming. This could be due to not having enough translational kinetic energy. |  |
| -3.1 | -5.1 | -413.977 | Reactive | The starting point starts at 200 pm between atoms A and B. Then the the atoms got closer and reaches the transition state. This is when the distance AB and BC are equal. Then the AB distance remains continuous while the BC distance begins to increase. The BC bond breaks and the AB bond forms. It only crosses the transition state once. It ends up in the products as the distance AB is short (molecule containing atoms A and B bonding) and BC is distance is long (reactant molecule BC bond has been broken). |  |
| -5.1 | -10.1 | -357.277 | Unreactive | The whole trajectory shows that it's unreactive because the starting point and ending point are similar. It started at a high AB distance value and also ended at a high AB distance value. This suggests this is end unreactive.
At the starting point, AB are far apart. Then they begin approaching each other and reach the transition state. However, they repel from each other and then start approaching each other again. This happens again and then the distance AB begins to increase again. The BC bond is formed again, resulting in the reactant molecule BC at the end. |
 |
| -5.1 | -10.6 | -349.477 | Reactive | This crosses the transition point more than once. It's reactive as it's end point is at a high BC distance and low AB distance, suggesting that the BC bond broke and the AB bond has formed resulting in AB + B.
From the starting point, the AB distance starts to decrease. This suggests atom A and B approach each other, but then the AB distance begins to increase again so the A and B atoms repel. There is a moment when the distance between atoms A and B is the same as the distance between B and C (transition state) Then the B and C atoms approach each other and then repel B continuously. While atoms A and B get closer forming a bond. The molecule AB vibrates while atom C continuously repels away from it. |
 |
OK. What do you conclude from the table? Mak214 (talk) 18:40, 29 May 2020 (BST)
Transition state theory
- Q5. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The three assumptions of the transition state theory[6] are:
1) The transition state will only be crossed over once. Once the transition state it reached, the products will be formed.
2) During the transition state, any motion along the reaction coordinate can be separate from the other motions and treated classically as a translation. The concentration of the transition state is in equilibrium with the reactants. (concentration constant relating them both, there's a Maxwell-Boltzmann distribution between the reactants and the transition state at any given time) This is defined as the Quasi equilibrium. It's assumed that the kinetic energy is predicted by the Boltzmann distribution. The transition states that are turning into products are distributed among their states according to the Maxwell-Boltzmann Laws[7] even in absence of an equilibrium between the reactant and product molecules.
3) There's minimum effects of quantum tunneling.
The quantum tunneling effect[8] is when the reactants can overcome the barrier by moving across it to turn into the products. The transition state theory doesn't include quantum tunneling. If quantum tunneling was included, it would increase the rate of reaction as more reactants will turn into products. There are only classical motions in the transition state theory. Hence it is suggested that quantum tunneling isn't included in the model used in Table 5 because it's assumed there's a faster alternative route used.
Additionally, in the Table 5 model the transition state theory wasn't true because the transition state was crossed over more than once in the last two reactions in Table 5, this could decrease the rate of reaction due to the products being able to cross the transition state again and go back into the reactants. Therefore, the transition state theory is an over-estimate in comparison to the model used. Yes. Good. Mak214 (talk) 18:41, 29 May 2020 (BST)
EXERCISE 2: F - H - H system
PES inspection
- Q6. By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
| r/ ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 500 | 0 |
| r(BC) | 70 | 0 |
In the following equations, A = atom F, B = atom H, C = atom H.
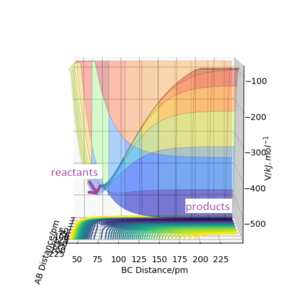
The initial conditions in Table 6 gives the potential energy diagram for Figure 7. The reason for this is because the F and H bond is very far apart, suggesting that it's not bonded whereas the hydrogen atoms are closer together, suggesting a F atom and H2 molecule are in the initial conditions.
Equation 2: F + H2 → HF + H is an exothermic reaction[9] shown in Figure 7. The energy of the reactants is higher than the energy of the products. This shows that this is an exothermic reaction due to the process releasing energy. This suggests that the bond strength of H2 is weaker than the bond strength of HF as no additional energy was required to break its bond. This reaction has an early transition state[10] due to the the fluorine atom being highly electro-negative so it attacks the hydrogen molecule very quickly.
| r / ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 70 | 0 |
| r(BC) | 500 | 0 |
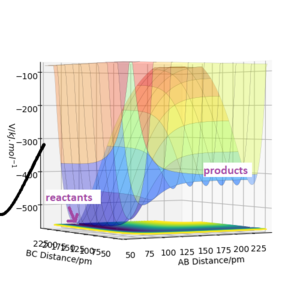
The initial conditions in Table 7 gives the potential energy diagram for Figure 8. The reason for this is because the F and H atoms are very close together compared to both the hydrogens. This suggests that a HF molecule and one H atom are in the initial conditions.
Equation 3: HF + H → F + H2 is an endothermic reaction[9] shown in Figure 8. The energy of the reactants is lower than the energy of the products. This suggests that this reaction is endothermic as the process used additional energy to break the H-F bond to form the H-H bond. Therefore, in the potential energy surface diagram there will be a lot of vibrational energy before the transition state compared to after. This also suggest that the HF bond is stronger than the HH bond as it requires additional energy to break its bond. This will give a late transition state.The translational energy could get converted into vibrational energy in order to break the bond between the strong H-F bond[11]. This favours the endothermic reaction because the reactants position will be aligned with the direction of the minimum energy path.
- Q7. Locate the approximate position of the transition state.
| r /ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 180 | 0 |
| r(BC) | 74.5 | 0 |
The transition state position shown in Table 8 was estimated by looking at the initial conditions in Table 6 for the exothermic F + H2 → HF + H reaction. Due to exothermic reactions having early transition states, this suggested that the bond distance BC (the hydrogen atoms) would be small as it's the reactant. The initial bond distance of AB was reduced until the hessian matrix, shown in Table 9, gave a value of Det= -1.0 <0 which proved it was a saddle point. Additionally, there was no force. This also suggested it was the transition state.
| AB direction | +1.000 | -0.024 |
| BC direction | -0.024 | -1.000 |
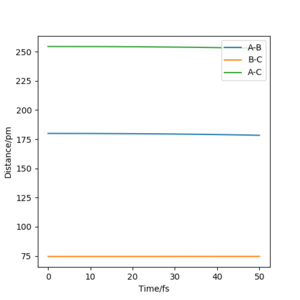
Additionally, Figure 9 shows the intermolecular distance vs time graph. This is a flat line, this could be due to everything in the system being stationary. There are no oscillations showing that there are any vibrational motions. This suggest that it's at the initial conditions in Table 8 represent the transition state position.
- Q8. Report the activation energy for both reactions.
Equation 2: F + H2 → HF + H the activation energy value is 1.0 kJ/mol.
Equation 3: HF + H → F + H2 the activation energy value is 126.7 kJ/mol.
The activation energy for equation 2 was calculated by getting the potential energy for transition state by using the initial conditions in Table 8. Then this was subtracted by the potential energy obtained by using the initial conditions in Table 10. Activation energy = TS(potential energy) - Reactants(potential energy) = (-433.981)-(435.056) = 1.075 kJ/mol
| r/ ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 500 | 0 |
| r(BC) | 74.5 | 0 |
The activation energy for equation 3 was calculated by getting the potential energy for for transition state by using the initial conditions in Table 8. Then this was subtracted by the potential energy obtained by using the initial conditions in Table 11. r(AB) which is the HF bond distance = 92 ppm[12]. The r(BC) bond which is the HH bond distance was set very high because the hydrogen atoms aren't bonded in the reactants.
Activation energy = TS(potential energy) - Reactants(potential energy) = (-433.981)-(560.698) = 126.7 kJ/mol
| r/ ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 92 | 0 |
| r(BC) | 500 | 0 |
Good work. well done. Mak214 (talk) 19:28, 29 May 2020 (BST)
Reaction dynamics
- Q9. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
| r/ ppm | p/ g.mol-1.pm.fs-1 | |
|---|---|---|
| r(AB) | 175 | -1.6 |
| r(BC) | 74 | 0.3 |
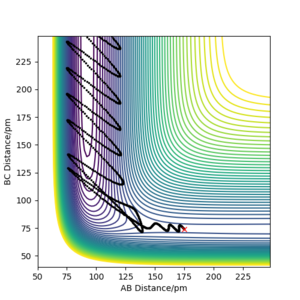
The step number was increased to 4000 and the initial conditions in Table 12 gives the potential energy surface diagram in Figure 10. This shows a reactive trajectory for the exothermic reaction F + H2 → HF + H as it passes the transition state as well as having many oscillations. The end point is also far away from the starting point.
The starting point (reactants) has a high energy level compared to the products due to being exothermic[9]. Hence the potential energy converts into translational kinetic energy. Therefore, there are many oscillations in Figure 10 due to energy being conserved.
This can be explained by the difference in distribution of the energy levels between an excited and relaxed state. The excited state will have an occupied ground state (v=0) as well as an occupied first state (v=1) where v=vibrational number. Whereas in the relaxed state only the ground state will be occupied. This approach uses the harmonic oscillator[13]. When energy is released, in the excited state there will be two transitions, v(0)→v(1) and v(1)→v(2), the fundamental peak and overtone. In the ground state it will only have transitions from v(0)→v(1).
Therefore, in an IR spectrum[14], for the excited state there will be two peaks corresponding to the overtone and fundamental peak. The overtone peak intensity will be smaller than the fundamental's peak intensity. Hence there are many oscillations due to the overtone decreasing and then increasing in intensity while the fundamental increases and then decreases in intensity.
Therefore, this could be confirmed experimentally by Infrared spectroscopy (IR).
- Q10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
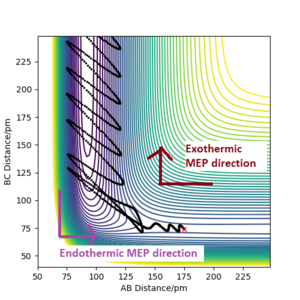
The position of the transition state affects whether the reaction is either exothermic or endothermic. An endothermic reaction will have a late transition state, suggesting that the vibrational energy efficiency will be higher[15]. The reason for this is because if it had a higher translational kinetic energy, the reactants wouldn't follow the minimum energy path and will just collide with each other but then immediately repel resulting in being back at the starting point. Hence, the translational kinetic energy converts into vibrational energy[11] instead so the reactants collide and are aligned with the minimum energy pathway. The direction of the path taken is shown in Figure 11. The initial conditions in Table 12 was used to give the reactive trajectory. This suggests that endothermic reactions have higher vibrational energy to make their reactions more efficient so it's able to overcome the transition state. Hence there are a lot of oscillations before the transition state is reached because it requires more efficient vibrational energy in order to reach the transition state.
Whereas if the reaction has an early transition state, it will be an exothermic reaction. This suggest that there will be a higher translational kinetic energy compared to vibrational energy. This means that there will be less oscillations before it reaches the transition state as shown in Figure 11.
Overall, an efficient endothermic reaction will have a higher vibrational energy whereas an efficient exothermic reaction will have a higher translational kinetic energy. Great. Please see a couple of comments of mine earlier on in the report. Otherwise I think this is a good job. Thank you especially for the extensive bibliography and for referencing throughout the text, good practice. Mak214 (talk) 21:40, 29 May 2020 (BST)
- ↑ Chemistry LibreTexts. 2020. 2.6: Potential Energy Surfaces. [online] Available at: <https://chem.libretexts.org/Courses/University_of_California_Davis/UCD_Chem_107B%3A_Physical_Chemistry_for_Life_Scientists/Chapters/2%3A_Chemical_Kinetics/2.06%3A_Potential_Energy_Surfaces> [Accessed 19 May 2020].
- ↑ Chemistry LibreTexts. 2020. Hammond’S Postulate. [online] Available at: <https://chem.libretexts.org/Bookshelves/Ancillary_Materials/Reference/Organic_Chemistry_Glossary/Hammond%E2%80%99s_Postulate> [Accessed 22 May 2020].
- ↑ Atkins, de Paula, Keeler: Physical Chemistry, 11th Edition. Section 18D.3 Potential Energy Surfaces (PESs)
- ↑ Evans, M.G. and Polanyi, M., 1938. Inertia and driving force of chemical reactions. Transactions of the Faraday Society, 34, pp.11-24.
- ↑ J. I. Steinfeld, J. S. Francisco, W. L. Hase Chemical Kinetic and Dynamics 2nd ed., 8.3.1, Prentice-Hall, 1998.
- ↑ J. I. Steinfeld, J. S. Francisco, W. L. Hase Chemical Kinetic and Dynamics 2nd ed., Chapter 10 pg. 20, Prentice-Hall, 1998
- ↑ Rowlinson*, J.S., 2005. The Maxwell–Boltzmann distribution. Molecular Physics, 103(21-23), pp.2821-2828.
- ↑ Abyss.uoregon.edu. 2020. Quantum Tunneling. [online] Available at: <http://abyss.uoregon.edu/~js/glossary/quantum_tunneling.html> [Accessed 22 May 2020].
- ↑ 9.0 9.1 9.2 Duff, J.W. and Truhlar, D.G., 1975. Effect of curvature of the reaction path on dynamic effects in endothermic chemical reactions and product energies in exothermic reactions. The Journal of Chemical Physics, 62(6), pp.2477-2491.
- ↑ Chemistry LibreTexts. 2020. Hammond’S Postulate. [online] Available at: <https://chem.libretexts.org/Bookshelves/Ancillary_Materials/Reference/Organic_Chemistry_Glossary/Hammond%E2%80%99s_Postulate> [Accessed 22 May 2020].
- ↑ 11.0 11.1 Polanyi, J.C. and Tardy, D., 1969. Energy Distribution in the Exothermic Reaction F+ H2 and the Endothermic Reaction HF+ H. The Journal of Chemical Physics, 51(12), pp.5717-5719.
- ↑ Cccbdb.nist.gov. 2020. CCCBDB Listing Of Experimental Data Page 2. [online] Available at: <https://cccbdb.nist.gov/exp2x.asp?casno=7664393&charge=0> [Accessed 22 May 2020].
- ↑ Cccbdb.nist.gov. 2020. CCCBDB Listing Of N2 Experimental Data Page 2. [online] Available at: <https://cccbdb.nist.gov/exp2x.asp?casno=7727379&charge=0> [Accessed 18 May 2020].
- ↑ Chemistry LibreTexts. 2020. 5.5: The Harmonic Oscillator And Infrared Spectra. [online] Available at: <https://chem.libretexts.org/Courses/Pacific_Union_College/Quantum_Chemistry/05%3A_The_Harmonic_Oscillator_and_the_Rigid_Rotor/5.05%3A_The_Harmonic_Oscillator_and_Infrared_Spectra> [Accessed 22 May 2020].
- ↑ Guo, H. and Liu, K., 2020. Control Of Chemical Reactivity By Transition-State And Beyond.