MRD:lydia

Exercise 1: H + H₂ system

In this exercise, all A, B and C atoms are hydrogen

Dynamics from the transition state region

Q1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The minima is points where the gradient equals to zero ( dV/dr_BC or dV/drAB equals zero). If you are making a sentence using is/are, you are making a definition. So you are saying, when the gradient equals to zero, it is a minima. But this is not true, because it could also be a maxima or a saddle point. I think what you meant is that when it is a minima, the gradient equals to zero. But can you see the difference?--Sw2711 (talk) 14:17, 17 May 2018 (BST)

The transition state is a stationary point of the potential energy surface (saddle point). The curvature of the transition state is negative. Yes, the TS is a stationary point and it is a saddle point. But by reading this sentence and the one above, you still haven't told me what is the difference between a minima and a TS(saddle point). Also, 'the curvature of the TS is negative', is it actually true? --Sw2711 (talk) 14:17, 17 May 2018 (BST)

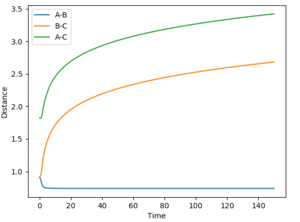
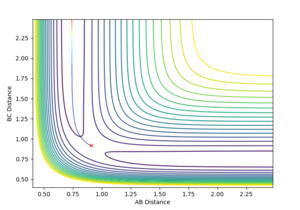
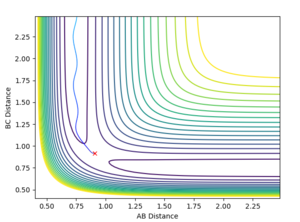
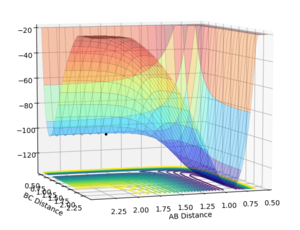
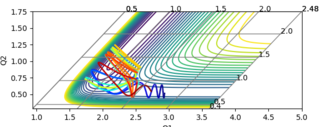
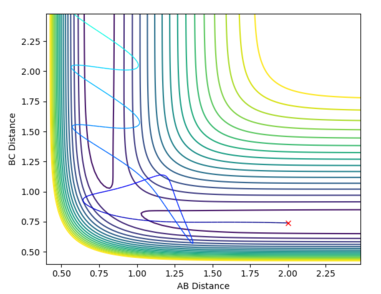
The gradient equals to zero when the potential energy curve reaches minimum points or maximum points. A picture of the potential surface plot is shown below. The bottom line on the curve is the line where the gradient dV/dr_BC equals to zero (the minimum energy path). Along the line, there are small peaks and troughs on the two sides. In the middle of the line, there is a comparatively large jump of the line, where we can find a point with a maximum value of the potential energy. This point corresponds to the transition point. At the transition point, the BC distance and the AB distance are the same while the momenta of AB and BC are zero That's not true. You can pass TS with some momenta, depending on your initial settings. --Sw2711 (talk) 14:17, 17 May 2018 (BST), the three atoms stop oscillating, as shown in figure 1 (the trajectory drawn is a single point). However, any point that is not the transition point will make the three atoms start oscillating, as shown in figure 2 (the trajectory drawn is an oscillating curve).

After reading this paragraph, I think you do understand where the TS is. But you still haven't told me clearly what is the difference between a saddle point and a local minima. Please check this video to see if it makes sense to you. link--Sw2711 (talk) 14:17, 17 May 2018 (BST)

figure 1. The transition point on the potential surface plot.

figure 2. Oscillating trajectory line on the potential surface plot

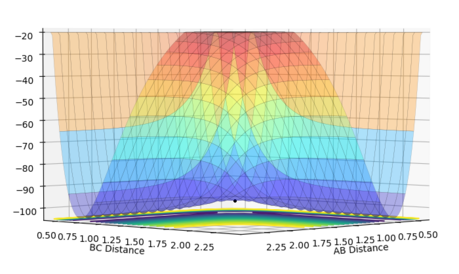Q2: Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

figure 3. Distance vs. Time graph when r=0.908

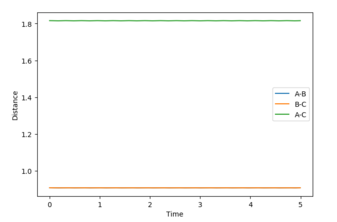
The best estimate of the transition state position r_ts would be 0.908. Normally, even giving zero initial momentum, one atom A would collide a diatomic molecule BC, the AB distance will decreases as A approaches to the BC molecule. Then, after the collision, the BC bond breaks and new bond AB form, thus, the BC distance would increase while AB distance decrease (changing oscillatory within a certain range). However, at the transition state position, the three atoms are in equilibrium positions, the distance between the three atoms would be be constant, So, if you set both distances to 0.91, it is a constant oscillation. There is no reaction and no intersection in distance. Why is 0.91 not a TS? Why do you think 0.908 is the closest to TS? --Sw2711 (talk) 14:21, 17 May 2018 (BST)

as shown in figure 3 (where the initial AB and BC distance set to 0.908).

Q3: Comment on how the mep and the trajectory you just calculated differ.

For MEP calculation method, it assumes that the atom experience no initial energy (it does not take the initial momentum into account), thus the atom will directly move to the direction with lower potential, with no oscillation. It is more than just the initial momentum. It actually re-set momenta to zero at each oscillation cycle. Otherwise, based on your assumption, you should expect the same trajectories produced by both Dynamics and MEP when you initial momenta are set to zero. But you don't. --Sw2711 (talk) 14:24, 17 May 2018 (BST) However, the dynamics calculation takes into account the initial momentum. Although the atom will still move towards the position with lower potential energy, they can still move slightly towards the position with higher potential energy due to the energy brought by initial momentum. Thus, the atoms are moving towards the lower potential energy position with oscillations.

	p1	p2	r1	r2	distance vs time	momentum vs time	Contour plot
MEP calculation	0	0	2.5 (sign of continue to increase)	0.74	figure 4 distance vs time, MEP	figure 5. momentum vs time MEP	figure 6. r1 is 918, r2 is 0.908, using MEP calculation
Dynamics calculation	2.5	oscillating around 1.2	infinity	oscillating around 0.74	figure 7. distance vs time dynamics	figure 8. momentum vs time dynamics	figure 9. r1 is 0.918, r2 is 0.908, using dynamics calculation

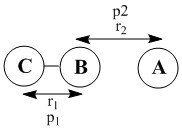
In reverse case (when r₁ is set to 0.908, r₂ set to 0.918), results are shown below:

	p1	p2	r1	r2
MEP calculation	0	0	0.74	2.5 (sign of continue increasing)
Dynamics calculation	oscillating around 1.2	2.5	oscillating around 0.74	infinity

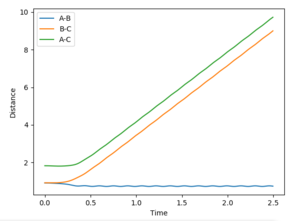
When setting a dynamic calculation with initial r₁=0.74, r₂=10, p₂=-2.5, p₁=-1.2, the distance vs time graph shows a rapid decrease of the r₂ value while the r₁ value oscillate slightly around the inital value. Until at large t, the r₁ and r₂ value approach to the same value.

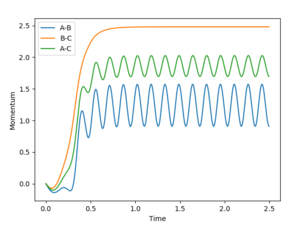
The momentum value for both p₁ and p₂ remain oscillating around the initial value, then increase rapidly at large t (at t=2.1).

figure 10. The distance vs time graph when the initial setting are r1=0.74, r2=10, p1=-1.2, p2=-2.5

figure 11. The momentum vs time graph when the initial setting are r1=0.74, r2=10, p1=-1.2, p2=-2.5

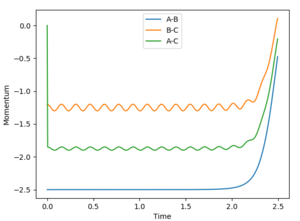Reactive and unreactive trajectories 

Q4: Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

Good for the detailed observation. My main question is 'What do you notice about the energy?' --Sw2711 (talk) 14:37, 17 May 2018 (BST)

	p1	p2	Total Energy	Reactivity	Description	Plot
1	-1.25	-2.5	-99.018	reactive	The AB distance decreases from 2 to the transition point, then further decreases to around 0.75 (with oscillations) and continue oscillating around 0.75. The BC distance remain unchanged until the transition point is reached, then increase rapidly to infinity. Bond formation between A and B leads to the formation of the excited vibrational AB molecular structure, thus, the AB distance oscillating.	figure 12.
2	-1.5	-2.0	-103.706	unreactive	The AB distance decreases oscillatory to the transition point, then increasing again (oscillatory) to infinity. The BC distance oscillates around 0.75, but not changing a lot (since the B-C bond is nor broken by the collision with atom A).	figure 13
3	-1.5	-2.5	-98.956	reactive	The AB distance decreases from 2 to the transition point, then further decreases to around 0.75 (with oscillations) and continue oscillating around 0.75. The BC distance remain unchanged until the transition point is reached, then increase rapidly to infinity. Compare to the first set of data, the oscillatory decrease before reaching the transition point is more rapid in this set of data.	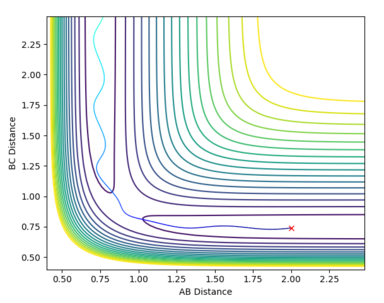figure 14
4	-2.5	-5.0	-84.956	unreactive	The AB distance decreases rapidly to the transition point, then oscillate around 0.8 for one cycle, then increase again to infinity. The BC distance oscillates largely around 0.75.	figure 15
5	-2.5	-5.2	-83.416	unreactive	The AB distance decreases rapidly to the transition point, then oscillate around 0.8 for one cycle, then increase again to infinity. The BC distance oscillates largely around 0.75. Although, the BC distance is oscillating, it oscillates outside the range of the typical H-H bond length value, thus there might not be actual bond forming. That's a really good point. But which status would this system get to when the time is long? --Sw2711 (talk) 14:37, 17 May 2018 (BST)	figure 16

Q5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Main assumptions of the transition state theory:

1. By examining the transition sate complex, the rate of reaction can be obtained.
2. The transition state complexes are in quasi-equilibrium with the reactants.
3. The products are formed through the transition state complex.

The predicted reaction rate would be longer than the experimentally obtained rate of reaction.

The transition state theory assumes that an activated complex can be formed at the transition state, and it is in equilibrium with the reactants. Thus, the transition state complex has to be longer lived in order to allow the quasi-equilibrium condition to be reached. However, in reality, the transition state complex is an activated complex with high energy and it is not too stable, most of them do not exist long enough for the quasi-equilibrium to be established (especially at high temperatures).

Also, the transition state theory assume all the atoms behave as the classical mechanics, the atoms have have to collide with sufficient energy for the reaction to proceed (the transition state can only be formed and the reaction is only possible if the activation barried is passed). However, in reality, the atoms can tunnel through the activation barrier, thus across it even without enough initial energy, which would lead to different pathways for the reaction to happen. This can also lead to a difference between the TST predicted rate of reaction and the experimentally obtained value.

For this part: I think the term ‘equilibrium’ is not very applicable here. ‘equilibrium’ is mainly used in statistical thermodynamics. So like…thinking about a reaction A+B<=>C. Statistically speaking there is 80% molecules in this system reacts from the left to the right and 20% the other way around. (about obviously you should think about more like a Boltzmann distribution ). This reaction has reached an equilibrium. But in terms of your system, there are only 3 atoms. So, it is either one way or the other. So you need to think about what TST means to your system. You haven’t really answered how will TST predictions compare with experimental results. --Sw2711 (talk) 14:37, 17 May 2018 (BST)

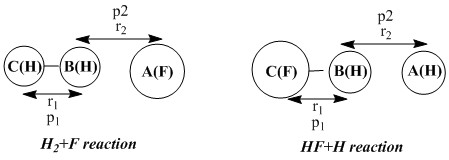
Exercise 2: F - H - H system

PES inspection

Q1: Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

For F + H₂ reaction to occur, the H-H distance (r₁) is set to 0.74 while the r₂ is set to 2.5. the p₁ was set to -1.0 and the p₂ as set to -14. the total reaction energy turns out to be -13.733. Thus, the reaction is exothermic, which indicates that the H-F bond strength is greater than the bond strength of H-H.

For H + HF reaction to occur, the HF distance (r₁) is set to 0.9 while the r₂ is set to 2.5. The p₁ was set to -1 and the p₂ was set to -13.5. Turns out the total reaction energy is +35.632. Thus, the reaction is endothermic, which also indicates that the bond strength of H-F is greater than the bond strength of H-H. Since the reaction involves the bond breaking of H-F (endothermic process) and the bond formation of H-H (exothermic process), the overall reaction endothermic would mean that the energy absorbed via H-F bond breaking overrides the energy released via the formation of H-H bond. Thus, H-F bond strength greater.

This is a very good method. Can you think of other methods to figure out whether it is endo or exo? Can you tell directly from an energy surface?--Sw2711 (talk) 14:39, 17 May 2018 (BST)

Q2: Locate the approximate position of the transition state.

I can see some pictures. But I need some explanations, pretending I am not the marker but a course mate about to start this lab next week. How would you explain to me what those figures mean?--Sw2711 (talk) 14:42, 17 May 2018 (BST)

	r1(rBC)	r2(rAB)	Potential surface plot	Distance vs Time
H2+F	0.746	1.810	figure 17. the potential surface plot and the trajectory of the transition state	figure 18. The internuclear distance vs time graph when the initial distance is set to the distance in the transition state
HF+H	1.810	0.746	figure 19. The potential energy surface plot and the trajectory of the transition state	figure 20. The distance vs time graph when the initial distance is set to the distance of the transition point

Q3: Report the activation energy for both reactions.

Reaction	Energy of the transition state	Energy of the reactant	Activation energy	Energy vs Time graph
H2+F	-103.751 kJmol-1	-103.778 kJmol-1	0.029 kJmol-1	figure 21
HF+H	-103.751 kJmol-1	-133.315 kJmol-1	30.036 kJmol-1	figure 22

When the initial structure was set to a structure near the transition state, the trajectory will fall down from the starting point to the reactant point, which leads to energy decrease from the activated transition point (the initial starting point) to the reactant point (the reactants are low in energy). Thus, the activation energy can be calculated as the difference between the transition state energy and the reactant energy. This part is good, because you have explained to me. --Sw2711 (talk) 14:43, 17 May 2018 (BST)

Reaction dynamics

Q4: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

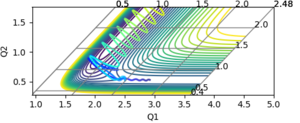
The reaction is possible if the initial condition was set as r₁(r_BC)=0.73, r₂(rAB)=1.79 while 0<p₁<-1.75, p₂=-8.

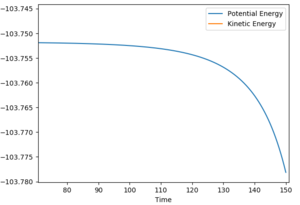
As shown in figure, the momentum of AB (p₂) oscillate vibrantly indicating that the AB (HF) molecule has gained kinetic energy.

figure 23. The momentum vs time graph of the system

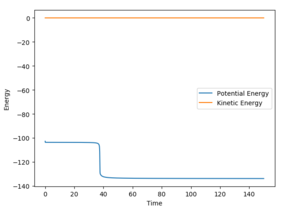
Thus, the reaction energy released is absorbed by the AB molecule, so that the AB molecule is excited into its excited vibrational state. After the absorption of the reaction energy, the energy of the system is interchanging between the potential energy and the kinetic energy, as shown in the figure below. This increase in the energy can be confirmed by calorimetry. Good, because you have shown me with evidence and explained--Sw2711 (talk) 14:44, 17 May 2018 (BST)

figure 24. Energy vs time graph of the system

Q5: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

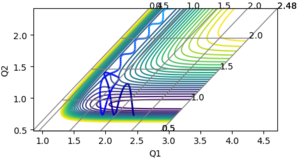
The Polanyi rules, which state that vibrational energy is more efficient in promoting a late-barrier reaction than translational energy, is further confirmed by the observation below.

The translational energy is increased via the increase of the AB momentum (A atom approach BC molecule faster) while the vibrational energy is increased via increasing the momentum of the BC molecule (the BC molecule vibrates more significantly).

This is not so true. If you think one momentum is equivalent to vibrational energy and the other momentum is equivalent to translational energy, this is not true. When you add the momentum into the system, you are just adding the kinetic energy. But whether this kinetic energy goes to translational or vibrational energy, you have some control, but not all of them. The best way to read the vibrational energy is to see how many contour lines the trajectory has passed (i.e. how far away it is from the minimum energy path). Therefore, changing the momentum of the molecule is not the only way to change the vibrational energy, you can also change your starting point (i.e. the molecule bond length). --Sw2711 (talk) 11:28, 18 May 2018 (BST)

Although both increasing the translational energy and the vibrational energy would increase the total energy of the system, the translational energy increase would more significantly increase the efficiency of the reaction (the reaction is more likely to proceed). As shown in the table below, for the same reaction with similar total energies, the one with higher vibrational energies (initial condition 1) does not proceed while the one with higher translational energy (initial condition 2) proceeds.

Good research on Polanyi rules and the experiments. But I just can't see how your experiments matches the Polanyi rule. You said in Polanyi rules 'vibrational energy is more efficient in promoting a late TS reaction than translational energy.' But in your experiments, you proved to me that 'translational energy is more efficient.' So, what is wrong? Is there anything missing or you forgot to explain?--Sw2711 (talk) 14:51, 17 May 2018 (BST)

	Initial conditions	energies	the skew plot	Reactivity
1	rHF=1.81 rHH=0.74 pHF=-0.5 pHH=-3	Total Energy=-96.111 kJmol-1 Higher vibrational energy Lower translational energy	figure 25. skew plot with high vibrational energy	unreactive
2	rHF=1.81 rHH=0.74 pHF=-0.8 pHH=-0.1	Total Energy=-103.475 kJmol-1 Higher translational energy Lower vibrational energy	figure 26. skew plot with high translational energy	reactive

The reaction that is endothermic would require higher vibrational energy input for the reaction to occur, as shown in the table below. With the similar amount of translational energy input (similar p₂ value), the F+HF reaction requires more vibrational energy (higher p₁ value) for the reaction to occur. Since the F+HF reaction is endothermic and the transition state energy is similar to the products energy (the transition state resembles more to the product than to the reactants), it could be concluded that the reaction with transition state closer to the product might need more vibrational energy for the reaction to occur.

So you think it is whether it is endothermic or exothermic which determines which type of energy is more efficient. Do you have any reference or theory to support that? --Sw2711 (talk) 14:54, 17 May 2018 (BST)

Inversely, since F+H2 reaction is exothermic and the transition state resembles more to the reactants,the reaction with transition state closer to the reactants might not have high vibration energy requirement.

reaction scheme	Initial conditions	Energies	Skew plot	Reactivity
F+H2	rHF=1.81 rHH=0.74 pHF(p2)=-0.8 pHH(p1)=-0.1	Total Energy=-103.475 kJmol-1 Lower vibrational energy	figure 27	reactive
H+HF	rHF=0.74 rHH=1.81 pHF(p1)=-0.8 pHH(p2)=-1.0	Total Energy=-103.205 kJmol-1 Higher vibrational energy	figure 28	reactive