MRD:lemon
Zy3915 (talk) 15:41, 4 May 2017 (BST)
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
zero. For a minimum point, the curve must go up for any direction starting from that minimum, while for a transition structure, the curve can either go up or go down from the point.
(What is zero? You need to discuss the mathematical definition of a Transition State --- what are the signs for the first and second derivatives of the Potential Energy Surface? How does a saddle point differ from a maximum or a minimum? The answer to this is literally in the script Je714 (talk) 15:58, 8 May 2017 (BST))
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
(you need to zoom out in both axes to make clear that the geometry is not varying with time. A range of 0.00001 time units and 0.0005 A will not show this Je714 (talk) 11:50, 9 May 2017 (BST))
Comment on how the mep and the trajectory you just calculated differ.
much fewer steps is required to complete a dynamics calculation (about 200) compared to that required by mep calculation(more than 5000)
Also, dynamics calculation gives a wavy line while the plot of mep shows no vibration.
(You're right about the difference in steps and the wavy line vs. no vibration. But why is that? Those are just mere observations, you need to be able to understand the reason behind them -- that's what this question is aiming for. Je714 (talk) 15:58, 8 May 2017 (BST))
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.
What do you observe?
the trajectory goes back the the transition state position.
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
- r1 = 0.74 and r2 = 2.0
| p1 | p2 | |
|---|---|---|
| -1.25 | -2.5 | reactive |
| -1.5 | -2.0 | unreactive |
| -1.5 | -2.5 | reactive |
| -2.5 | -5.0 | unreactive |
| -2.5 | -5.2 | reactive |
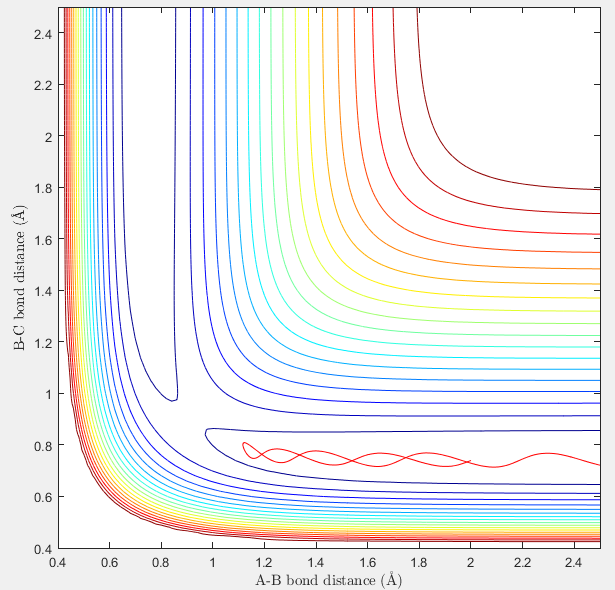
r1 = 0.74; r2 = 2.0; p1=-1.25; p2=-2.5: reactive The particles have the right energy in this case that allows the two molecules to reach the transition state and separate with the atom A breaking the old B-C diatomic bond and forming a new A-B bond.
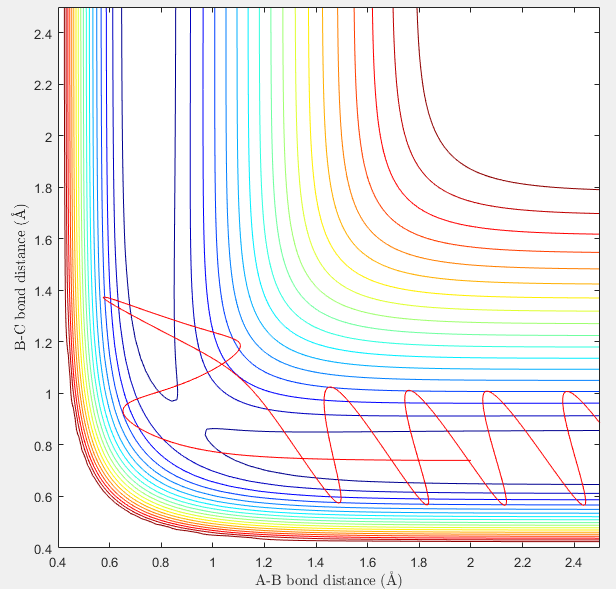
r1 = 0.74; r2 = 2.0; p1=-1.5; p2=-2.0: unreactive The relative momentum of atom A is not high enough fro it to reach the diatomic molecule B-C to get to the transition state, therefore it bounces back.
r1 = 0.74; r2 = 2.0; p1=-1.5; p2=-2.5: reactive This case is very similar to the first case that the momenta are all quite low and the atom A has enough energy to reach transition state and then allows the reaction happen mildly.(no much vibration observed on the trajectory.)
r1 = 0.74; r2 = 2.0; p1=-2.5; p2=-5.0: unreactive Both particles have high momenta therefore although a transition state is formed, it collapse back into the originally atom A and diatomic B-C.
r1 = 0.74; r2 = 2.0; p1=-2.5; p2=-5.2: reactive This case is the opposite to the fourth case in consequence. the momentum of atom A is slightly higher than before so eventually it overcomes the high energy barrier for transition state and then a new molecule of A-B is formed
State what are the main assumptions of Transition State Theory. Given the results you have obtained,
how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory assume that the motion of the atoms obey classical mechanics. In reality, molecular vibrations are quantized so the predicted rate might be higher than the experiment value as mostly of the molecules don't have enough energy to reach higher vibrational level for forming a new bond.
(This is not the only assumption of TST. What about recrossing of the TS? You've observed that in your previous experiments. Je714 (talk) 18:20, 8 May 2017 (BST))
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 is a exothermic reaction while H + HF is endothermic. This fact HF has stronger bond than H2 and therefore F + H2 are less stable than H + HF.
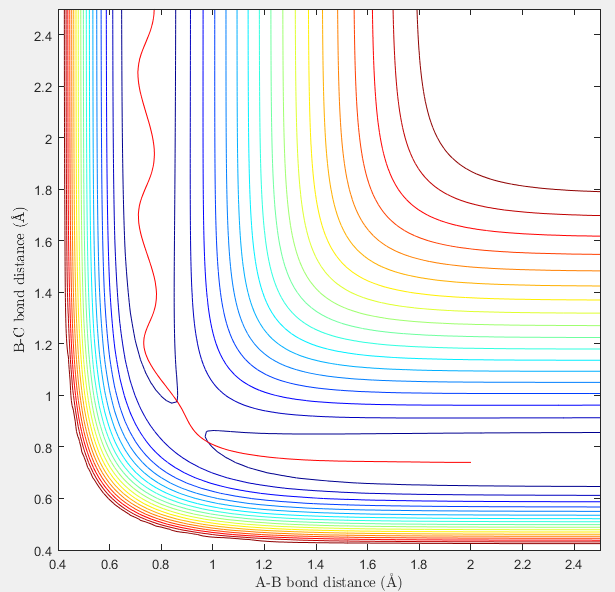
Locate the approximate position of the transition state.
At transition state, r1=1.815A r2=0.74A approximately.
(Some evidence for this would be needed Je714 (talk) 16:04, 8 May 2017 (BST))
Report the activation energy for both reactions.
for reaction F + H2 Ea=-0.2 kcal/mol for reaction H + HF Ea=-30.2 kcal/mol
(How have you reached these numbers? Have you tried using MEP? Are you sure they are negative?Je714 (talk) 16:04, 8 May 2017 (BST))
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
r1 = 2.5; r2 = 0.74; p1=-0.983; -0.399<=p2<=-0.583 Significant fluctuation on momentum of A-B which means the energy released from H-F bond forming was converted to the vibrational energy of HF molecules. Experimentally, an increase in temperature in a closed systems should be observed as the progressing of the reaction.
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe? Note that we pare putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.
The system is reactive when pHH<-2.8 or pHH>2.8, where the vibrational energy of the H-H bond is high enough to break for the reaction to go forwards.
For the same initial position, increase slightly the momentum pFH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.1. What do you observe now?
when the kinetic energy of F is high enough, the system can be reactive no matter how low the vibrational energy of H2 is.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The distribution of energy between translation energy and vibrational energy is always more efficient when the modes with higher energy barrier is satisfied. In other words, it is more effective to break the bond first by adding more vibrational energy when a strong bond needs to be break. On the other hand, the position of the transition states tells which mode helps more for the reaction to happen: when the transition state is close to the reactant, it means the bonding is relatively easy to break so that more energy should be given to the transnational energy for the particles to meet each other.
(Good. Some examples of these situations are needed to prove your explanations. Also references to Polanyi's empirical rules. Je714 (talk) 18:20, 8 May 2017 (BST))