MRD:lec17
EXERCISE 1: H + H2 system
Dynamics from the transition state region
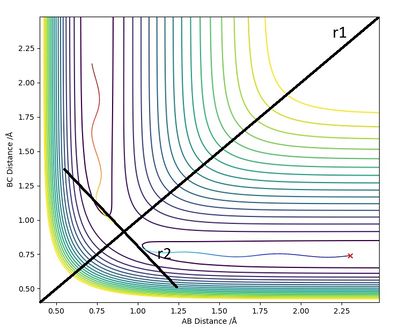
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is the maximum on the minimum energy path linking reactants and products, this is observed as a saddle point. At this point the first partial derivative is equal to zero (∂V(ri)/∂ri=0). The second partial derivatives of the saddle point with respect to the orthogonal vectors (see diagram - r1 and r2 where r2 is the tangent to the minimum energy pathway at the transition state ) are of opposite signs where r1 is positive and r2 is negative. The negative value of the second partial derivative will correspond to the maximum, whereas the positive value of the second partial derivative will refer to the maximum. I think you mean minimum. Also how can you distinguish it from a local minimum? Pu12 (talk) 18:02, 6 June 2019 (BST)
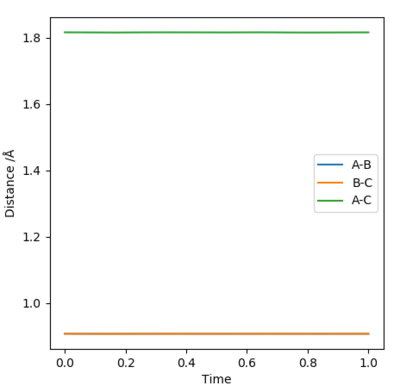
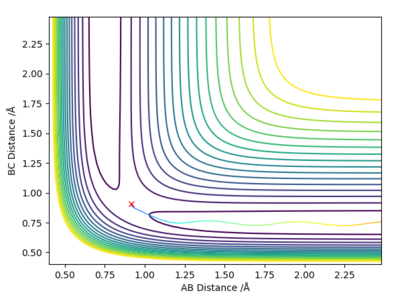
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
Using AB distance = BC distance and a momentum of 0, a plot can be produced of internuclear distances vs time. The values for the distances were optimised to produce a graph with no trajectory towards the products or reactants and with minimal oscillation. This distance value was found to be 0.9079 angstroms and so this is a good estimate for the transition state position.
Comment on how the mep and the trajectory you just calculated differ.
The minimum energy path corresponds to infinitely slow motion and so the momenta are reset to zero each step. This means that in comparison to the dynamics calculation graph (right hand photo) the energy pathway on the mep graph (left hand graph) shows fewer oscillations.
 |
 |
Reactive and unreactive trajectories
Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Yes | The reactants collide with enough energy to cross the activation barrier and form the products. Vibrational energy is shown in the products by the oscillations displayed on the illustration. | 
|
| -1.5 | -2.0 | -100.456 | No | The reactants collide but there is not enough energy for them to cross the activation barrier. As a result, the molecules do not pass through the transition state. | 
|
| -1.5 | -2.5 | -98.956 | Yes | The reactants collide with enough energy to cross the activation barrier and so the molecules cross through the transition state. | 
|
| -2.5 | -5.0 | -84.956 | No | The reactants collide and have enough energy to cross the activation barrier, however, due to the large amounts of energy they recross the barrier and return to the reactants. | 
|
| -2.5 | -5.2 | -83.416 | Yes | The reactants collide and have enough energy to cross the activation barrier. There is a large amount of vibrational energy in the products and so there is a possibility for barrier recrossing, however, the reaction goes to completion. | 
|
The table demonstrates how even when reactants collide with enough energy to reach the transition state, a reaction may not necessarily occur as barrier recrossing is possible. This means that the reaction between those molecules may not go to completion, despite having enough energy. This means therefore that the effective rate of reaction of a sample of molecules would likely be lower than the theoretical prediction as not all of the collisions with enough energy will produce a reaction. Good.Pu12 (talk) 18:02, 6 June 2019 (BST)
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
There are many assumptions involved in Transition State Theory, particularly:
- The electronic and nuclear motions are separate.
- The equilibrium Boltzmann distribution is used to describe the energy distribution of the reactants throughout the reaction.
- There is no barrier recrossing possible - once the molecules have passed the transition state in the direction of the products, the reactants cannot be reformed.
- In the transition state, motion along the reaction coordinate may be separated from all other motions.
- Even if there is no equilibrium between the reactants and the products, the activated complex is still distributed according to the Boltzmann distribution (the quasi-equilibrium postulate).
The limitations of Transition State Theory mean that the predictions for reaction rate values may not match the experimental values. An example of this is how TST assumes that barrier recrossing is not possible, however, the results produced in the previous question show that barrier recrossing does indeed occur in experimental systems. This would mean therefore that the predicted values for the reaction rate would be higher than the experimental values, as it would assume that all the collisions with enough energy would result in a reaction that went to completion.
EXERCISE 2: F - H - H system
PES inspection
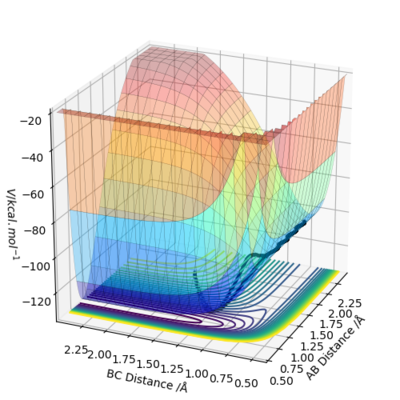
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
 |
 |
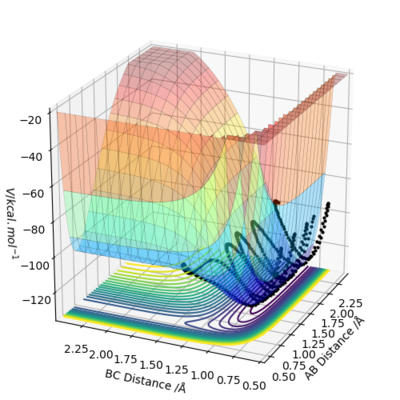The surface plot for H + HF starts at a low energy level and needs to gain a large amount of energy to reach the transition state, reaching a higher energy level at the products. This therefore suggests that this is an endothermic reaction. Conversely, the surface plot for F + H2 starts at a higher energy level and has a decrease in energy to reach the energy level of the products. This reaction is therefore exothermic. The endothermic nature of the H +HF reaction demonstrates how the H-H bond formed in the products is weaker than the H-F bond in the reactants. This is similarly shown in the exothermic reaction between F and H2 which shows how the H-H bond being broken in the reactants is weaker than the H-F bond being formed in the products. Good.Pu12 (talk) 18:02, 6 June 2019 (BST)
Locate the approximate position of the transition state.
According to Hammond's Postulate, in an exothermic reaction the transition state will most closely resemble the reactants as it is closer to them in energy. Similarly, in an endothermic reaction the transition state is closer in energy to the products and so will most closely resemble them. The momentum for AB and BC was set to 0, and the AB and BC distances were gradually changed until a graph of internuclear distances vs time is produced with minimal oscillation and no trajectory towards either the reactants or the products. The distances to produce this were found to be 1.813 angstroms for H-F and 0.7445 angstroms for H-H. Therefore, rts(H-F)=1.813 angstroms and rts(H-H)=0.7445 angstroms.
 |
Report the activation energy for both reactions.
 |
 |
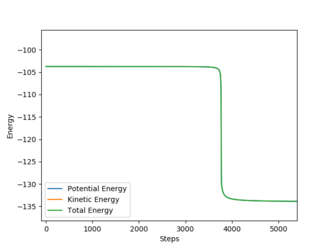Activation Energy(H + HF)= +30.013 kcal mol-1
Activation Energy(F + H2)= +0.245 kcal mol-1
Reaction dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
Initial conditions were found that gave a reactive trajectory. These were an AB distance of 0.74 angstroms, a BC distance of 1.81 angstroms, an AB momentum of -2.5 and a BC momentum of -1.69. This produces the Momenta vs Time graph shown below.
 |
 |
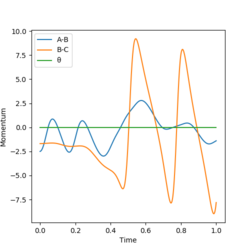It can be seen that the number of oscillations increases in BC over time, which shows that the energy in the reaction is converted to kinetic energy of BC. This agrees with the graph of energy over time where, whilst the total energy stays constant, the kinetic energy slightly increases and the potential energy slightly decreases. When the potential energy decreases, the kinetic energy increases and vice versa. The reaction between H2 and F is exothermic and so the kinetic energy is converted to heat energy, which would be displayed experimentally as an increase in temperature.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's rules state that vibrational energy is much less efficient in promoting an early-transition state reaction than translational energy, and vice versa for a late-transition state reaction. It was shown above that the reaction of H2 and F is an exothermic reaction and so according to Hammond's postulate this reaction has an early transition state. Conversely, the reaction of HF and H is endothermic and so according to Hammond's postulate has a late transition state. Taking into account Polanyi's rules, the reaction of H2 and F should be most effectively activated by translational energy and the reaction of HF and H should be most effectively activated by vibrational energy.
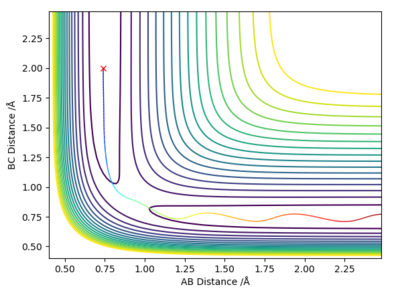
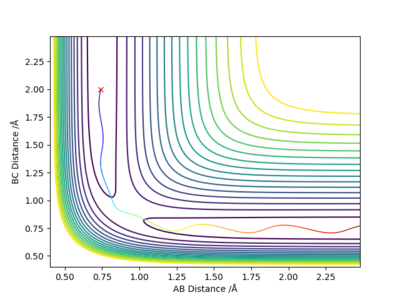
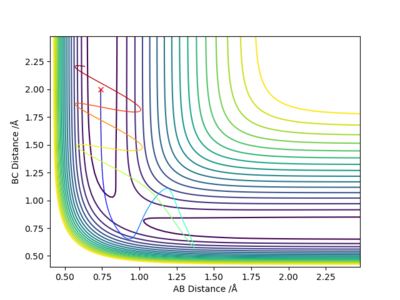
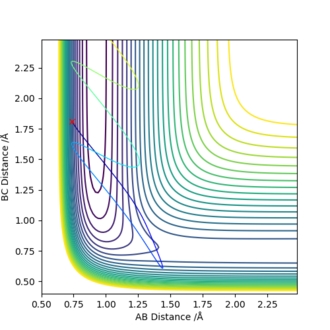
For the reaction of H2 + F, the values of rHH=0.74 angstroms and rHF=1.81 angstroms were used. The left hand figure below shows the contour plot when pAB=-2.5 and pBC=-0.5, this figure relates to greater vibrational energy. The right hand figure shows the contour plot when pAB=-0.5 and pBC=-2.5, this figure relates to greater translational energy. It can be seen that the figure for greater translational energy displays a successful trajectory, whereas the figure for greater vibrational energy shows an unsuccessful trajectory - this, therefore, agrees with Polanyi's rules for an early transition state reaction.
 |
 |
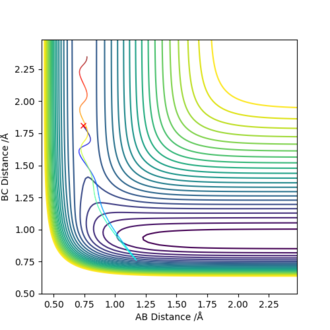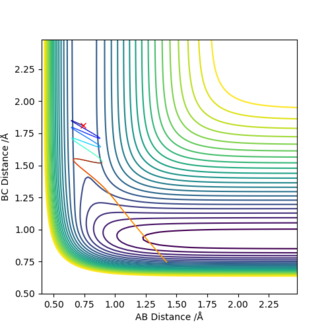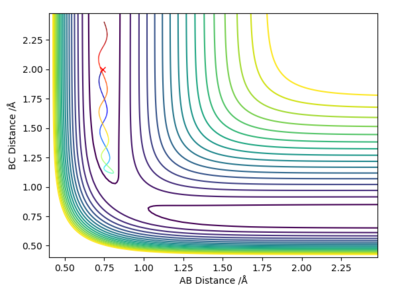
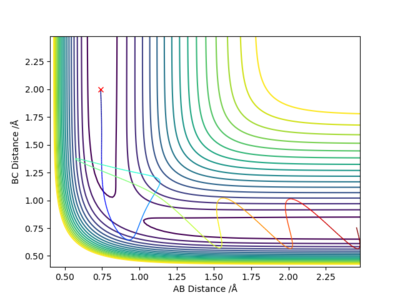
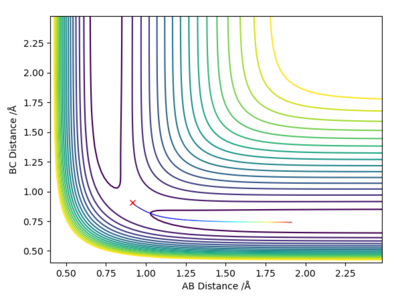
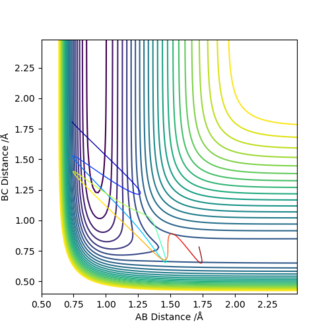
For the reaction of HF and F, the values of rHF=0.74 angstroms and rHH=1.81 angstroms were used. A contour plot was produced for a situation with greater translational energy, pHF=-0.5 and pHH=-2.5 (left-hand figure), which was shown to be an unsuccessful trajectory. A contour plot for greater vibrational energy was also produced, where pHF=-2 and pHH=-0.75 (right-hand figure), which displays a reactive trajectory. According to Polyani's empirical rules, we would expect the reaction to be most effectively activated by vibrational energy as this reaction has a late transition state. The graphs produced, therefore, support this.
 |
 |
Good report with good illustrations, well done.Pu12 (talk) 18:02, 6 June 2019 (BST)