MRD:kk3015
Molecular Reaction Dynamics:
Exercise 1: H + H2 System
The total gradient of the potential energy surface is zero for both the minimum and the transition point as they are both turning points of the plot. The difference is that the absolute minimum has a second derivative that is positive in all directions, while the transition structure point is a saddle point, meaning that its second derivative is positive in one direction and negative in the other direction.
(This only applies to a 2-coordinate PES Tam10 (talk) 15:27, 22 May 2017 (BST))
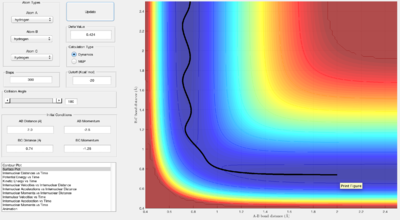
Through trial and error, the best estimate of the transition state position is at rts ≈ 0.908 Å. With this r value, the Internuclear Distance vs Time graph is:
As the graph shows, the system doesn't oscillate at rts = r1 = r2 = 0.908 Å, therefore this must be the transition point. This is because the trajectory started with no initial momentum, and so it will remain at the transition state forever.
.PNG)
.PNG)
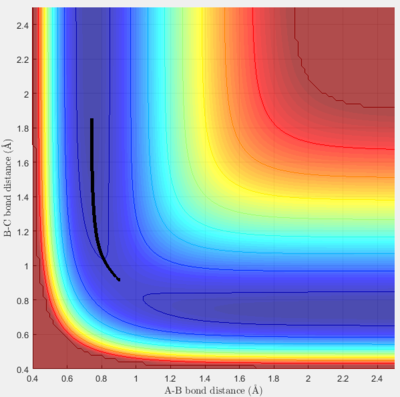
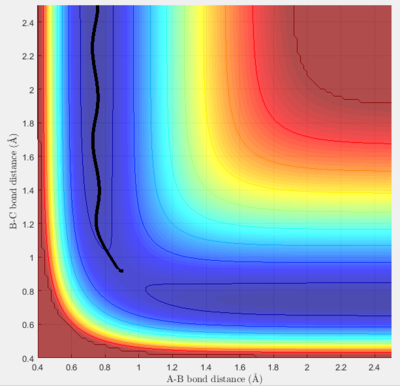
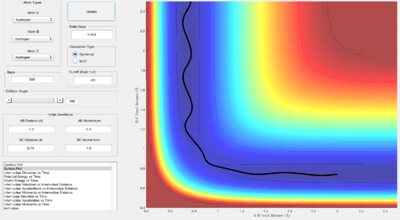
The MEP algorithm takes only the minimum point, requiring more steps and hiding the oscillating pattern. Whereas the Dynamics algorithm shows the oscillating pattern as the trajectory leads off with the B-C bond (r1) "breaking" and the product A-B "forming".
(But why does it do this? Tam10 (talk) 15:19, 22 May 2017 (BST))
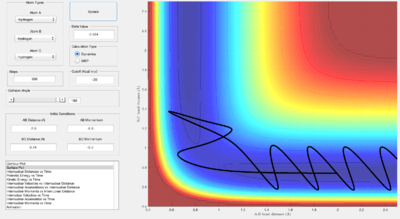
Looking at the "Internuclear Distances vs Time" and "Internuclear Momenta vs Time" graphs, still with r1 = rts + 0.01 and r2 = rts, the final values of r1(t) r2(t) and p1(t) p2(t) at large t (t = 15 s, 3000 steps), came to be:
t = 15 s, r1(t) = 55.51 Å, r2(t) = 0.7563 Å, p1(t) = 2.481, and p2(t) = 1.306
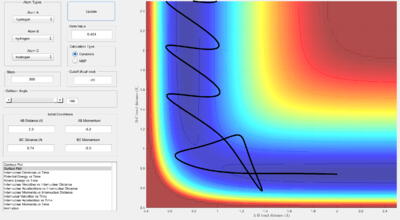
If the initial conditions are reversed, the reaction path now gradually rolls towards the reactants side instead of the products, giving the opposite values of r1(t) r2(t) and p1(t) p2(t):
t = 15 s, r2(t) = 55.51 Å, r1(t) = 0.7563 Å, p2(t) = 2.481, and p1(t) = 1.306
Setting up a calculation (Dynamics) with the initial positions corresponding to the final positions above but with the initial momenta having the opposite sign:
r1(t) = 55.51 Å, r2(t) = 0.7563 Å, p1(t) = -2.481, and p2(t) = -1.306
This gives us the graphs with the same curves but after being rotated 180°, meaning that the projectile simply came back to the old initial position.
Reactive and unreactive trajectories
| p1 | p2 | Reactive or Unreactive | Screenshot | Description |
|---|---|---|---|---|
| -1.25 | -2.5 | Reactive |  |
There is enough energy to overcome the kinetic activation barrier, causing the trajectory to roll towards the product. |
| -1.5 | -2.0 | Unreactive |  |
There is not enough energy to overcome the kinetic activation barrier, causing the trajectory to roll back towards the reactants. |
| -1.5 | -2.5 | Reactive |  |
There is enough energy to overcome the kinetic activation barrier, causing the trajectory to roll towards the product. |
| -2.5 | -5.0 | Unreactive |  |
There is enough energy to overcome the kinetic activation barrier, however the trajectory rolls back towards the reactants due to "barrier recrossing". |
| -2.5 | -5.2 | Reactive |  |
There is enough energy to overcome the kinetic activation barrier, causing the trajectory to roll towards the product; however the trajectory crosses the barrier twice before ending up rolling towards the products. |
The transition state theory assumes that, upon collision, the reactants will be in the right orientation resulting in a successful reaction and go on to form the products. Therefore, with enough energy to overcome the kinetic activation barrier, the rates in the obtained results will be higher than the experimental value due to the fact that not all reactant molecules will collide with the correct orientation, and so 100% successful collision rate is impossible.
Exercise 2: F - H - H System
Due to the fact that fluorine is much more electronegative than hydrogen, the H-F bond is much more polarised and stronger than the H-H bond. The energy required to break the H-H bond is lower than the energy released in the H-F bond formation, making the F + H2 reaction exothermic. And the energy required to break the H-F bond is higher than the energy released in the H-H bond formation, making the H + HF reaction endothermic.
Once again, from trial and error, the transition state position is approximately obtained to be:
AB(HF) = 1.812 Å, and BC(HH) = 0.745 Å
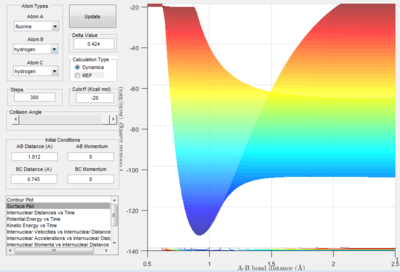
From the graph above, the activation energy for F + H2 is estimated to be around 30.2 kcal/mol, while the activation energy for H + HF is around 0.4 kcal/mol.
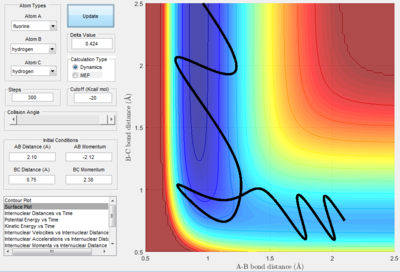
With the initial conditions set at AB(HF) = 2.10 Å, BC(HH) = 0.75 Å, p(AB) = -2.12, and p(BC) = 2.38, the F + H2 trajectory is reactive; as seen in the surface plot above.
From looking at the "Internuclear Momenta vs Time" graph and considering the conservation of energy, a transfer between translational and vibrational energy can be seen. Here, the energy released is transferred to vibrational energy in the new H-F bond, seen as an oscillating H-F(A-B) internuclear momentum after the transition state.
(The energy comes from potential energy, not translational Tam10 (talk) 15:19, 22 May 2017 (BST))
Polanyi's empirical rule states that, for a reaction with an early transition state, the translational energy is more effective in increasing the efficiency of the reaction than the vibrational energy. And vice versa for a reaction with a late transition state.
Looking at how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, using the "Internuclear Momenta vs Time" graphs:
F + H2:
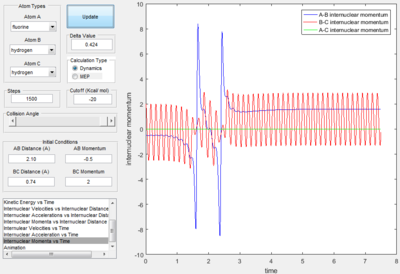
When the initial conditions were set with a small translational energy of -0.5 and a large vibrational energy of 2, the collision is unsuccessful; as seen by the above graph's continuing oscillation of the same B-C internuclear momentum line after the collision point.
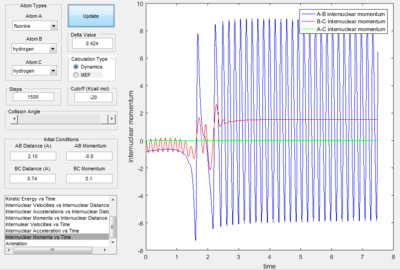
However, when the initial conditions were set so that the translational energy was larger (-0.8) and the vibrational energy was made smaller (0.1), the collision becomes successful; as seen by the oscillation transferring from the red line to the blue line after the collision point. This suggests that the reaction has an early transition state.
H + HFː
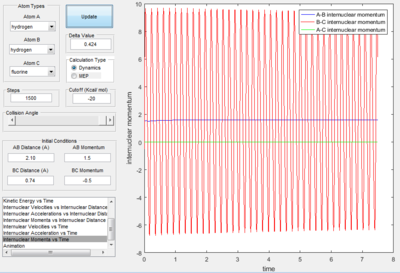
When the initial conditions were set with a large translational energy of 1.5 and a small vibrational energy of -0.5, the collision is unsuccessful; as seen by the above graph's continuing oscillation of the same B-C internuclear momentum line after the collision point.
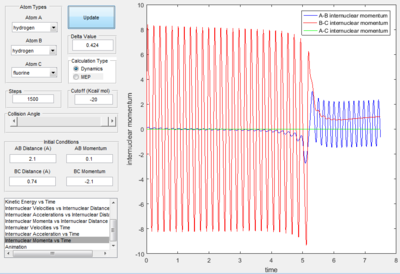
However, when the initial conditions were set so that the translational energy was smaller (0.1) and the vibrational energy was made larger (-2.1), the collision becomes successful; as seen by the oscillation transferring from the red line to the blue line after the collision point. This suggests that the reaction has a late transition state.
(What about the experimental question? Tam10 (talk) 15:19, 22 May 2017 (BST))