Molecular Reaction Dynamics: Applications to Triatomic systems

Part 1: H + H2 system

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The total gradient of the potential energy surface is zero at a minimum and at a transition structure.

When the second derivative of a stationary point is positive, the point is the minima. This is the point which has the smallest value compared to the the points nearby, showing a "valley.

For the transition structure, there is a saddle point in the potential energy surface. In terms of curvature, the gradient goes from (+) to 0 then (+) or from (-) to 0 then (-) again.

In which directions? Use the sign of second partial derivatives to be more precise with your definition. http://mathworld.wolfram.com/SecondDerivativeTest.html Je714 (talk) 17:28, 31 May 2017 (BST)

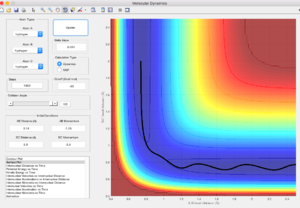
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

At transition state, r=0.908A. This is the radius that gives least oscillation when the momentum of both particles are zero. Going lower or higher than this value will cause the system to oscillate. The non-oscillating system shows that r=0.908A is the stationary point, where it is at the unstable equilibrium, slight increase or decrease in radius causes the system to fall to the stable equilibrium.

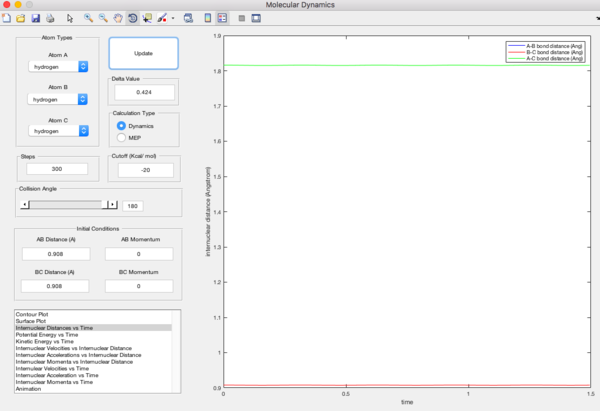
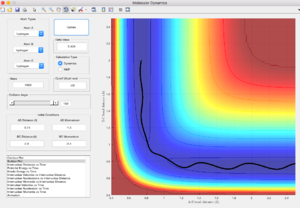
Radius at which least oscillation is obtained.

**Comment on how the mep and the trajectory you just calculated differ.**

Minimum energy path (mep) gives trajectory which follows the floor of the valley, non-oscillating whereas dynamic gives oscillating trajectory.

In mep, the velocity is always reset to 0. Therefore, the atom will accelerate and move in the direction of steepest descent at each time step. Hence, it will follow the floor of the valley, minima of the potential surface.

In dynamic trajectory calculation, at each time step, the atom has an initial velocity. Therefore, its motion is the coupling of the initial velocity and the acceleration due to the direction of steepest descent, which results in the oscillating path.

Good Je714 (talk) 17:29, 31 May 2017 (BST)

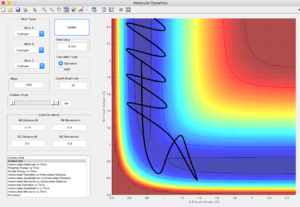
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

Condition	p1	p2	Reactivity	Comments
1	-1.25	-2.5	Reactive	Atoms have sufficient energy to pass through the transition state. New B-C bond is formed and oscillates due to vibrations.
2	-1.5	-2.0	Unreactive	Atoms approach each other but energy is not high enough to pass through transition state.
3	-1.5	-2.5	Reactive	Atoms have sufficient energy to pass through the transition state. New B-C bond is formed and oscillates due to vibrations. Higher magnitude of vibration of A-B due to higher kinetic energy. (Higher momentum, higher KE, KE=p²/2m)
4	-2.5	-5.0	Reactive but returns to initial state	Atoms have sufficient energy to pass through the transition state but the products returns to the initial state by recrossing the transition state.
5	-2.5	-5.2	Reactive	Atoms have sufficient energy to pass through the transition state twice, forming products.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Quasi-equilibrium assumption

When the reactants and products are not in equilibrium with each other, the activated complexes are in quasi-equilibrium with the reactants.

The flux of activated complexes in the two directions are independent of each other.

Each intermediate is long-lived enough to reach a Boltzmann distribution of energies before continuing to the next step.

Unless atoms or molecules collide with enough energy to form the transition structure, then the reaction does not occur.

The reaction system will pass over the lowest energy saddle point on the potential energy surface.

By obtaining the ΔG^≠ from the trajectory, the rate could be predicted using the Arrhenius equation. The value can hence be compared with the experimental values.

The 1st and 3rt points don't apply here -- we're simulating a triatomic collision in isolation, not an ensemble of particles. You need to talk about barrier recrossing, which is what you observe in some of the previous examples. You forgot to say if you expect the calculated reaction rate values to be higher or lower than the experimental ones. Je714 (talk) 17:32, 31 May 2017 (BST)

Part 2: F-H-H system

Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

1) F + H₂-> HF + H , exothermic

2) H + HF -> H₂ + F , endothermic

Need to relate this to the PES, if possible Je714 (talk) 17:32, 31 May 2017 (BST)

The exothermic reaction in 1 suggests that H-F bond is stronger than H-H bond. Since the formation of more stable or stronger bond in the product releases more energy than formation of weaker bond. This yields larger release in energy in 1 compared to 2. This is in agreement with literature BE (H-F) = 565 kJ mol^-1 , BE (H-H) = 432 kJ mol^-1.

Locate the approximate position of the transition state.

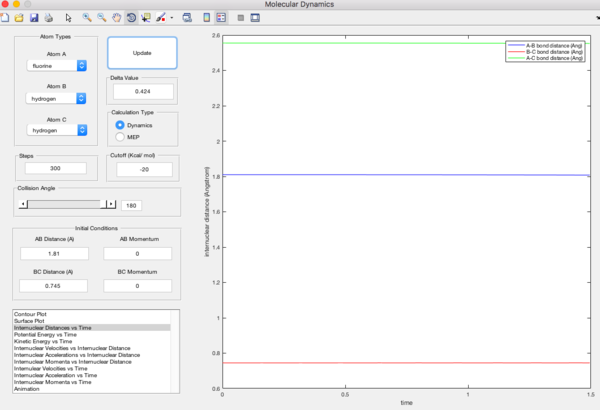
r_HF = 1.81A

r_HH = 0.745A

Report the activation energy for both reactions.

Energy of transition state = -103.3 kcal mol^-1

Energy of HF and H = -133.9 kcal mol^-1

Energy of H₂ and F = -104 kcal mol^-1

Thus,

Reaction 1: E_a = 0.7 kcal mol^-1 (lit. 1.6 kcal mol^-1)

Reaction 2: E_a = 30.6 kcal mol^-1

Δ_rH (Reaction 1) = -29.9 kcal mol^-1 (lit. -31.9 kcal mol^-1)

Precise estimate of final energy

Potential Energy vs Time	Energy / kcal mol^-1
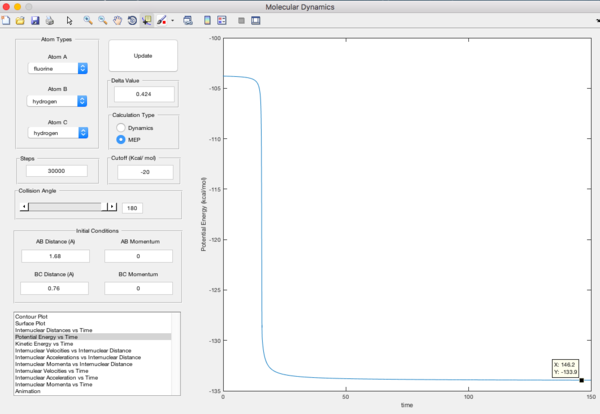
	-133.9
	-104

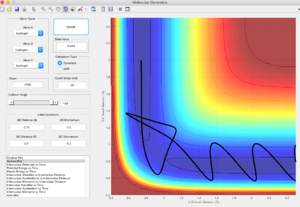
Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

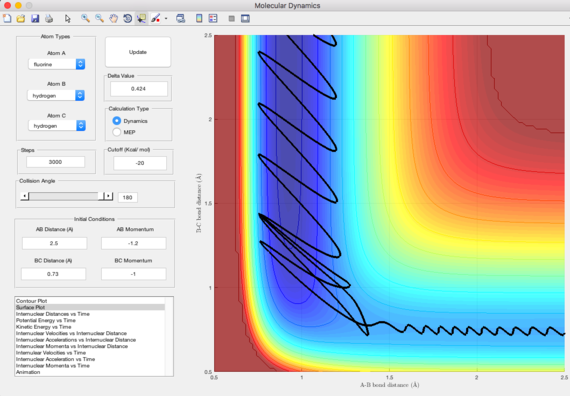
Initial conditions are r_HF = 2.5 A, r_HH = 0.73 A, p_HF = -1.2, p_HH = -1

From the internuclear momenta-time graph, H-H changes from small oscillatory vibration to a straight line, whereas H-F changes from straight line to large oscillatory vibration.

Therefore, due to the conservation of energy, the energy released is stored as vibrational energy in H-F. The system goes from small vibrational energy of the reactant to large vibrational energy of the product. The reaction is exorthermic, an increase in temperature of the reaction mixture indicates the reaction is successful.

Infrared chemiluminescence can be used to confirm the release of vibrational energy. It refers to the emission of infrared photons from vibrationally excited product molecules immediately after their formation. The intensities of infrared emission lines from vibrationally excited molecules are used to measure the populations of vibrational states of product molecules.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

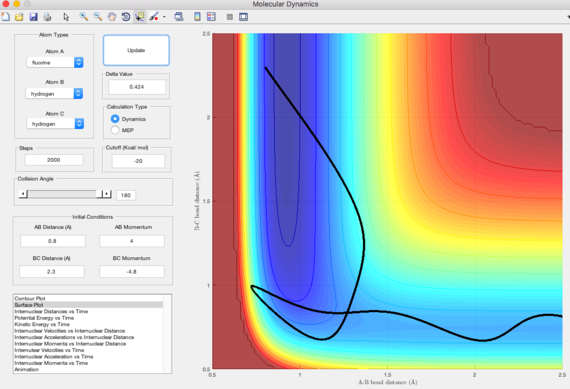
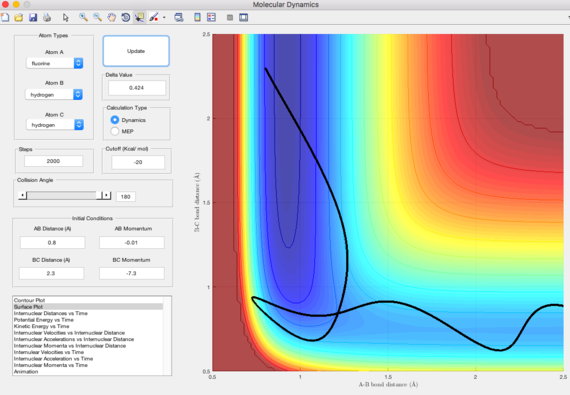
By using the equation KE=p²/2m, the kinetic energy of high p(HH) is much higher than low p(HH). This means that lower amount of input energy is needed for low p(HH).

Polanyi's rules state that vibrational energy is more efficient than translational energy in promoting reactions with late transition states. This would imply to reactions which are endothermic according to the Hammond's postulate. This is shown in the trajectories above, where low p(HH) requires less initial energy for the reaction to be reactive when the energy is stored in the vibrational motion of H-F. Thus, exothermic reactions are more energetically efficient when the reactant energy is stored in the translational mode, whereas endothermic reactions are more energetically efficient when the reactant energy is stored in vibrational mode.

Do you have examples of the opposite case? Je714 (talk) 17:33, 31 May 2017 (BST)