MRD:kb4817

3/5 - Some very good aspects to this report, but there were one or two large gaps in your understanding which needed to be corrected. See comments below.

Molecular Reaction Dynamics

H₂ + H

H₂ + H Transition State

The transition state on a potential energy surface diagram is defined as the point where the derivative (gradient) of the both reactant's and product's potential is 0 with respect to their bond distances. This can be further defined by taking the second derivative to establish whether it is a maxima or minima where a result less than one is minima and vice versa. The peak should be a maxima on the minimal energy pathway (MEP). The associated forces acting on both bonds, AB and BC, at this point are 0, which allows you to distinguish between other local minima where one of the bonds will not have zero force energy.

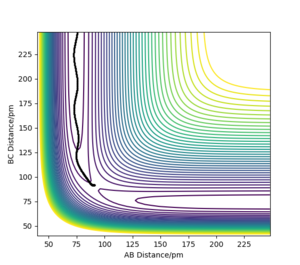
For a homo-nuclear reaction, the transition state is identified by the intersection of A-B and B-C as seen in Figure 1 where the bond distances are equal causing the forces acting on them to equal 0.

You're on the right track but you're still missing some important points. What mathematical structure does the TS resemble and how does this affect the gradient?

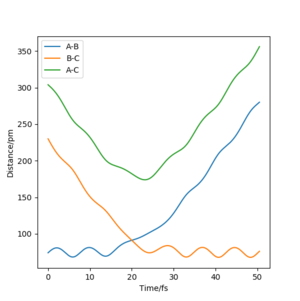
This intersection is at approximately 90.78 pm as shown by the single dot of the function representing 'gradient = 0' in Figure 2.

Correct estimate for the TS, well done

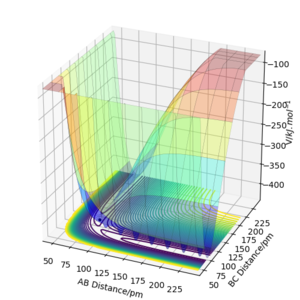
To identify other transition states, the atoms involved in the reaction will be stationary therefore change in momentum is zero and therefore so is the derivative. So by calculating the bond distances for which these are zero you can calculate the transition state. Hammond's postulate also states that if a reaction is exothermic the TS will resemble reactants and vice versa.

Trajectories

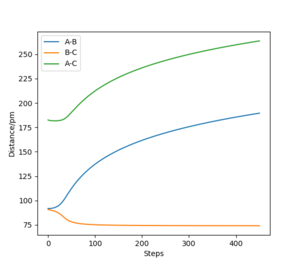
When calculating the MEP compared to the dynamic pathway of a reaction the main variable is the lack of oscillations of the bond lengths (i.e the vibrations between atoms). As we see in the AB bond, which is one pm longer than the BC bond, the vibrations of the bond length affect the inertia of atoms, however in the MEP the time steps always reset momenta to zero regardless of vibration and so vibrations are not observed. Both trajectories go towards forming the BC bond. MEP corresponds to purely translation energy whereas dynamic plotting corresponds to both translation and symmetric vibration.

Absolutely correct, well done!

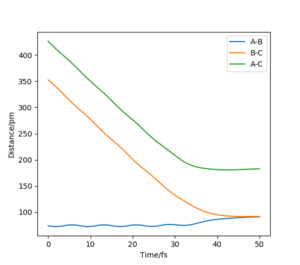
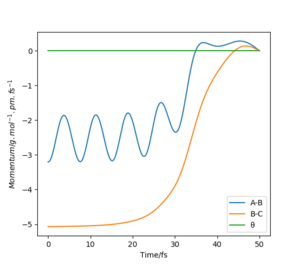
This can be further highlighted by the Figure 5 and Figure 6 where distance and momenta oscillate for dynamic and not MEP. For AB=BC + 1 pm at time t=40 for Figure 5 AB=280.22 pm, BC=73.76 pm, and Figure 6 p_AB=5.02 g.mol^-1.pm.fs^-1, p_BC=2.34 g.mol^-1.pm.fs^-1.

For BC=AB + 1 pm at last geometric point, the exact opposite occurs AB=74.03 pm, BC=352.60 pm, and p_AB=3.20 g.mol^-1.pm.fs^-1, p_BC=5.06 g.mol^-1.pm.fs^-1.

If we then plotted these final values as initial values and reversed the sign of momentum we obtain Figure 9, Figure 10 and Figure 11. We see that atom C approaches AB but never reacts and ends up at the same starting position as the initial reaction conditions.

Actually it looks like they've basically reached the TS all over again! This is exactly what should happen, assuming that the positions/momenta aren't rounded off.

*Figure 10: Dynamic Internucleic distances*

**Table of reactivity of different momenta but values AB=74 pm, BC=200 pm**
p_AB/g.mol^-1.pm.fs^-1	p_BC/g.mol^-1.pm.fs^-1	E_TOT/(kJ.mol^-1)	Reactive?	Description of Dynamics
-2.56	-5.1	-414.280	YES	AB + C -> A + BC where purely translation energy in initial approach of C develops oscillations due to the bond having formed and vibrating.
-3.1	-4.1	-420.077	NO	C approaches AB, however not enough energy to overcome activation energy therefore no reaction
-3.1	-5.1	-413.977	YES	Same outcome as first reaction with AB having slightly higher momenta and C having same momenta resulting on overall higher energy used in reaction
-5.1	-10.1	-357.277	NO	Reaction AB + C -> A + BC does occur, however it quickly dissolves back into the original reactants. This is called barrier recrossing. Recrossing is defined as passage over the potential barrier separating the two species followed by return to the original side¹.
-5.1	-10.6	-349.477	YES	Reaction occurs but also undergoes barrier recrossing twice. This therefore yields the products A + BC.

Transition State Theory

Overall the theoretical values of Transition State Theory (TST) underestimate the experimental values. This is due to assumptions made in TST that are not true when analysing in quantum mechanically.

This is incorrect. TS theory overestimates the rate of reaction. This is because the no-recrossing assumption (assumption 1 in your list) is a much stronger assumption than any other. QM tunneling is a weak effect, even for light atoms, and has an inverse dependence on mass, meaning that it becomes even less significant moving away from hydrogen. Your other assumptions are also not as relevant as (1). Think about why assumption (1) leads to an overestimation.

Assumptions made by TST:

1) R ⇌ TS -> P : Once there is enough energy to form the transition state (activation energy) the TS will form the products and no back reaction occurs

2) There is no quantum tunneling effect which essentially allows a slight bypass of the activation energy maxima

3) There is a quasi-equilibrium between reactants and transition state meaning there is a Boltzmann distribution between the two at any given time²

As TST treats the rate classically no quantum tunneling is factored in. The rate is therefore an underestimation as tunneling would provide a lower entry barrier for the formation of products and therefore more can be formed at a given time. It also assumes that TS molecules live long enough to form a Boltzmann distribution, which isn't true for many reactions so once the TS is formed it forms the products. This also assumes that we are dealing with a bulk amount reactants we are dealing with however the program being used only considers one molecule. It also assumes that at higher temperatures it still only passes through the energy maxima in the minimum energy pathway, however due to the increased energy of the system access to higher transition states are now available.

F + H₂ and FH + H systems

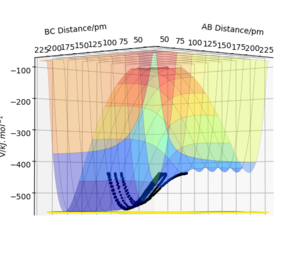
F + H₂ is exothermic and FH + H is endothermic. This tells us that the F-H bond is stronger than the homo-diatomic H-H bond as energy is released when forming F-H and energy must be put in to break this bond and form H-H instead. We observe this through the surface plot Figure 12 where the potential well of HF (AB) at lower bond distances is much deeper than that of H-H (BC) at lower bond distances.

Transition State

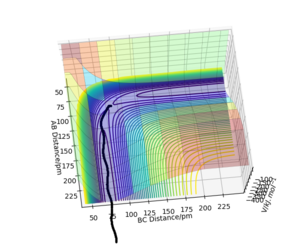
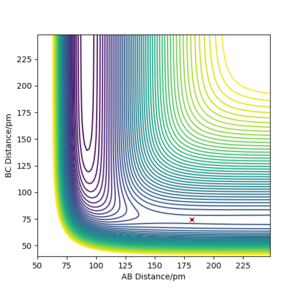
The approximate transition state position will be where both momenta equal zero and the forces acting on AB and BC are zero at given bond distances. The distances for this system are F-H=AB=181.15 pm and H-H=BC=74.49 pm as seen in Figure 13 and Figure 14. This was located using the Hessian matrix where one eigenvalue had to be positive and close to one and the other eigenvalue negative and close to 0.

Activation energy

To calculate activation energy, AB was plotted on a transition state MEP contour graph as normal and then BC was given a very large value to completely separate the two and vice versa for BC calculation. The last geometry of this was then plotted to establish the energy of reactants. These were then subtracted from the transition state energy to give the activation energy. In the case of F + H₂ (1) and FH + H (2) , the total energy of (1) is calculated and subtracted from the transition state energy to give the exothermic activation energy, and total energy of (2) subtracted from the transition state energy to give the endothermic activation energy. An alternative method to work out the energy of reactants is to -1 pm from AB whilst not changing BC and observe the dip into the well and vice versa as shown in Figures 15,16,17, and 18.

*Figure 15: Contour plot for F + H₂ Reactants*

*Figure 16: Energy v Time plot for F + H₂ Reactants*

*Figure 17: Contour plot for FH + H Reactants*

*Figure 18: Energy v Time plot for FH + H Reactants*

**Activation energies**
Reactants (R)	Endo/exothermic	E_TOT/(kJ.mol^-1)	Activation Energy/(kJ.mol^-1)
TS	N/A	-433.981	N/A
FH + H	Endo	-560.617	126.636
F + HH	Exo	-435.059	1.078

Good estimates for Ea in both directions, well done!

Reaction Dynamics

The reaction F + H₂ is exothermic and releases radiative heat as a result. This temperature increase is due to the increased vibrations of the newly formed F-H, which must compensate for the excess energy as it is itself buried deeper in energy (conservation of energy principle). This can be seen in Figure 15 where the momenta of the newly formed AB(=F-H) oscillates. To test this you could take the IR spectrum of the sample before and after it has reacted to see an initial peak in ground state of the molecule and once it reacts an overtone appears which is smaller and at lower wavenumbers (due to asymmetric overlap of anharmonic levels). This overtone decreases to 0 over time as all the molcules return to the ground state.

A set of reaction conditions where AB=FH=175 pm, BC=HH=74 pm, and p_AB= -1.6 g.mol^-1, p_BC= +0.2 g.mol^-1 allows a reaction to take place where the oscillations of the FH molecule are observed afterwards

Good answer. What other techniques can you think of?

*Figure 19: F-H-H Reaction system Contour graph*

*Figure 20: F-H-H Reaction system Momenta Time graph*

Polanyi's empirical rules state: vibrational energy is more efficient in promoting a late-barrier reaction (transition state resembling products) than translational, whereas the reverse is true for an early barrier reaction³. The reaction FH + H is endothermic and has a late transition state. Therefore, vibrational energy should encourage the formation of products and form them at a greater rate.

Correct.

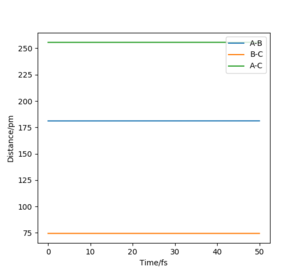
If we take an example for endothermic reaction H + HF, where there is a late transition stage, and plot AB=FH=91 pm and BC=HH= 100 pm, and p_AB= -0.1 g.mol^-1, p_BC= -5 g.mol^-1 we see there is no reaction (Figure 20). When the H collides with FH, it hits with too much force and in a straight line and so bounces further back then the original position which means it is too far for it form a HH bond, even if the translational energy is greater than the activation energy. When we have higher vibrational energy, its motion aligns more in the direction of the products as its orthogonal to the MEP. For an exothermic reaction, translational energy means the trajectory can fall to the lower energy region. Vibrations complicate this trajectory as it is in a different direction to the MEP.

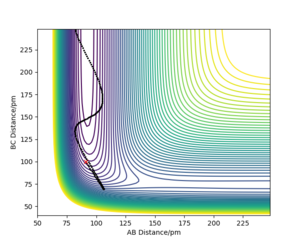
*Figure 21: Contour graph for low vibration, high translation energies*

I also need examples for the inverse case here as well.

Bibliography

1) Recrossings and Transition-State Theory; Huw O. Pritchard; The Journal of Physical Chemistry A 2005 109 (7), 1400-1404; DOI: 10.1021/jp045262s

2)Current Status of Transition-State Theory; Donald G. Truhlar, Bruce C. Garrett, and Stephen J. Klippenstein; The Journal of Physical Chemistry 1996 100 (31), 12771-12800; DOI: 10.1021/jp953748q

3)Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction; Zhaojun Zhang, Yong Zhou, Dong H. Zhang, Gábor Czakó, and Joel M. Bowman; The Journal of Physical Chemistry Letters 2012 3 (23), 3416-3419; DOI: 10.1021/jz301649w