MRD:jw13918
EXERCISE 1: H+H2 system
Dynamics from the transition state region
- On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
Answer:
On a potential energy surface diagram, the transition state is on the maximum of the minimum energy path, which is the saddle point. On this point, the gradient of potential energy is zero, and it can be defined mathematically as ∂V(ri)/∂ri=0. ri could represent both r1 and r2 in this case because this saddle point on energy path links both reactants and products in two directions separately. In H+H2 system, r1=r2 at transition state.
This response is fine but I'm not exactly sure what you mean in this last part "this saddle point on energy path links both reactants and products in two directions" ? the TS is a minimum with respect to the direction defined by r1 equals r2 which is a diagonal line on your plot, this corresponds to the equilibrium bond distance for the HHH species. Mak214 (talk) 17:18, 13 May 2020 (BST)
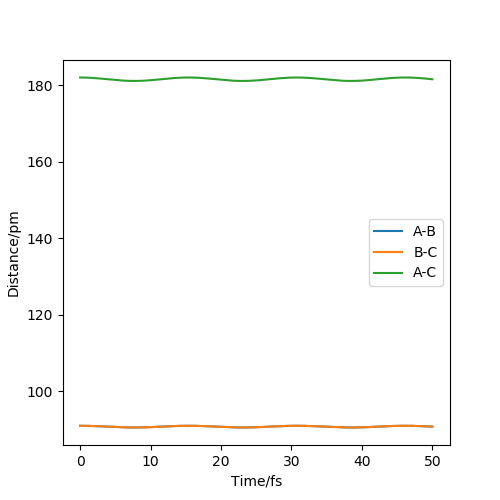
- Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
Answer:
To locate the transition state of the reaction, the first step was to check the main range of rts on the saddle point, and the range was r=80-100 pm. Then the initial conditions were changed into r1=r2, p1=p2=0.0 g.mol-1.pm.fs-1, and the r value was testing in the range. Finally, the best transition state position was found at rts =91 pm. If the trajectory starts at this point, it will not fall off due to no gradient, and the distance between the atoms will not change. So r1 and r2 is always constant at 91 pm. This can be shown in a "Internuclear Distances vs Time" plot below.
I can still see some oscillation which means you start slightly away from the TS. You can optimise the value of r further until there is no oscillation. Otherwise - this is a good response.Mak214 (talk) 17:00, 13 May 2020 (BST)
- Comment on how the mep and the trajectory you just calculated differ.
Answer:
When the calculation type is MEP, the mep shows that the trajectory falls off from the valley floor to H1+ H2-H3 smoothly, and the distance between H2 and H3 is almost constant. When the calculation type is Dynamics, the trajectory still falls off from the valley floor to H1+ H2-H3, but the distance between H2 and H3 oscillates slightly because the molecule has vibrational energy. Also, the distance between H1 and H2 increases to a larger value in dynamics calculation type than that in MEP calculation type. The reason is that the atoms have mass and they have inertia when they are moving. Therefore, the atoms will move further in reality.
Yes. Did you notice also that the intertia gets reset to 0 after every step in the MEP trajectory? This is a way to look for a nearby minimum on the potential energy surface. Mak214 (talk) 17:05, 13 May 2020 (BST)
Reactive and unreactive trajectories
- Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
Answer:
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | reactive | The trajectory moves smoothly to transition state first and then falls off to products with slight oscillation. | The diatomic reagent does not have vibrational energy so the distance between the two atoms does not oscillate. The diatomic product has vibrational energy so the distance between the two atoms oscillates. |
| -3.1 | -4.1 | -420.077 | unreactive | The trajectory shows the atom moves closer to the diatomic molecule until one point first, but goes back further from the point. | The momentum between the atom and diatomic molecule (p2) is not large enough to make enough kinetic energy to overcome the activation barrier. |
| -3.1 | -5.1 | -413.977 | reactive | The trajectory moves to transition state with slight oscillation first and then falls off to products with larger oscillation. | The diatomic reagent has a small vibrational energy so the distance between the two atoms oscillates slightly. The diatomic product has larger vibrational energy so the distance between the two atoms oscillates obviously. |
| -5.1 | -10.1 | -357.277 | reactive | The trajectory is very disordered. It moves to products first and then bounces back vigorously. | The momentum is too large so that the diatomic molecule (product) vibrates too vigorously to break the bond. The activation barrier is recrossed and It goes back to the reagents again. So is this a reactive trajectory afterall? Mak214 (talk) 17:21, 13 May 2020 (BST) |
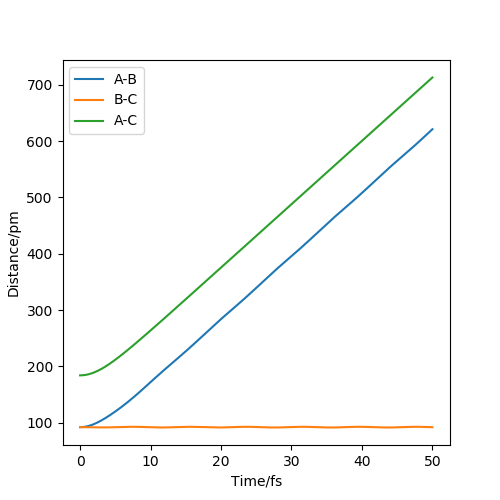
| -5.1 | -10.6 | -349.477 | reactive | The trajectory moves to products first and then bounces back a little. Finally it falls off to product with vigorous oscillation. | The momentum of the diatomic product is even larger than above one, so it vibrates more vigorously and breaks the bond but bounces back to diatomic product again. |
The figure below shows the last set of conditions in the table. The trajectory moves to products first and then bounces back a little. Finally it falls off to product with vigorous oscillation.
From the table, we can know that the momenta condition should be controlled in a range to make the trajectory reactive. If the momenta are too small, the system has no enough kinetic energy to overcome activation barrier, and the reaction cannot happen. If the momenta are too large, the activation barrier will be recrossed and the system will go back to reagents. But it may bounce back to product again if momenta is larger.
- Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Answer:
The reaction rate value by Transition State Theory predictions will be larger than experimental value. OK, yes. It would be good to have more discussion here where you relate your conclusion to the results you have seen. Mak214 (talk) 17:25, 13 May 2020 (BST)
EXERCISE 2: F - H - H system
PES inspection
- By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
Answer:
The F + H2 reaction is exothermic, and H + HF reaction is endothermic. The bond strength of HF is very high because it is hydrogen bond between a H atom with a more electronegative atom F, which is dipole-dipole interaction. The bond strength of H2 is relatively lower because it is non-polar covalent bond. Therefore, it will release heat while HF bond is formed from breaking H2 bond, and it will absorb heat while breaking HF bond to form H2 bond. We've only got one dipole here - I think you're thinking about intermolecular interactions when you say "dipole-dipole". Did you have a look at how this insight is translated into the potential energy surface (PES) of this system H + H + F? A bit of expansion on how you can see that the reactions are exothermic and endothermic from the PES would be good here. Mak214 (talk) 17:57, 13 May 2020 (BST)
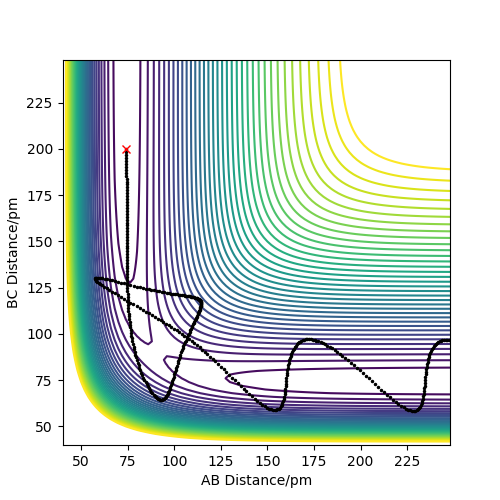
- Locate the approximate position of the transition state.
Answer:
The position of transition state is at around rts = 92 pm. The diagram below shows that the distances between atoms are flat on this transition state position. Now you are no longer dealing with a system where r1 and r2 are equal at the transition state! So you need two values rFH and rHH to define the transition state. The image below doesn't show what you describe. Mak214 (talk) 17:33, 13 May 2020 (BST)
- Report the activation energy for both reactions.
Answer:
The activation energy is equal to the difference between the potential energy of reagents and the potential energy of transition state. In the F + H2 reaction, the potential energy of reagents is about -550 kJ/mol, and the potential energy of transition state is about -500 kJ/mol. So the activation energy is (-500)-(-550)= 50 kJ/mol. In the H + HF reaction, the potential energy of reagents is about -580 kJ/mol, and the potential energy of transition state is about -450 kJ/mol. So the activation energy is (-450)-(-580)= 130 kJ/mol. Your answer for the second system is pretty good but way off for the first(about 1 kj/mol for this one). I think the image above is for the HHH system.Mak214 (talk) 17:57, 13 May 2020 (BST)
Reaction dynamics
- In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
Answer:
In F + H2 reaction, when the H-H bond is broken and H-F bond is formed, the bond length increases so that the potential energy will be in lower value. Since energy is conserved, the lost potential energy will be converted into reaction energy released. Then, it causes the exothermic reaction. That can be confirmed experimentally, and we can feel the temperature of reaction mixture increases while the system is releasing heat to the environment. A bit more description of the setup of this experiment would be useful. What about Vibrational energy? How does that factor in to this answer? Watch the animations again to get a really clear understanding of this - it's a useful descriptor for you to try to understand what is going on. Mak214 (talk) 17:57, 13 May 2020 (BST)
- Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Answer:
In H + HF reaction, when the vibrational energy of H-F bond (low momentum) is very low and translational energy of HH (high momentum of incoming H atom) is very high initially, it is difficult to obtain a reactive trajectory. If the vibrational energy of H-F bond is increase to a much higher level (higher momentum) and the momentum of the incoming H atom is decreased to a much lower level, and pHF is larger than pHH, we can obtain a reactive trajectory that from H + HF to H2 +F. If the position of the transition state is on a large distance of atoms, low vibrational energy and high translational energy will bring a reactive trajectory. Inversely, if the position of the transition state is on a small distance of atoms, high vibrational energy and low translational energy will bring a reactive trajectory. Good. Mak214 (talk) 17:57, 13 May 2020 (BST)
Thank you for engaging in the lab and answering all questions in your wiki page. Good to see the references included. I think you could benefit from going back over the HHF system exercises to really solidify your understanding of the distribution of energy. Some clearer answers are more careful calculation of the activation energy using the values obtained from the python program were required for full marks in this lab. Mak214 (talk) 17:57, 13 May 2020 (BST)
References
1 John C. Polanyi and Jerry L. Schreiber, in Faraday Discussions of the Chemical Society, 1977, 62, 267-290.
2 PetersBaron, in Reaction Rate Theory and Rare Events Simulations, 2017