MRD:jht114
Part 1: H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total gradient at the minimum and the transition structure are both 0.
For minima, the second derivative wrt to the quantity in consideration will be greater than zero. In the potential energy surface, this is the lowest point in the region where the surface shows a 'valley'.
For the transition structure, there will be a saddle point in the potential energy surface, which is the maximum of the minimum energy path linking the reactants and products. In terms of the curvature, the potential surface first decreases/increases to 0, then decreases/increases again.
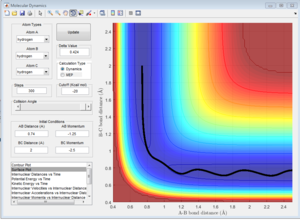
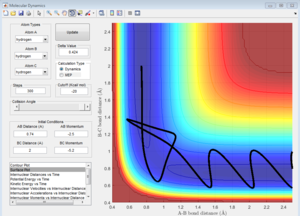
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
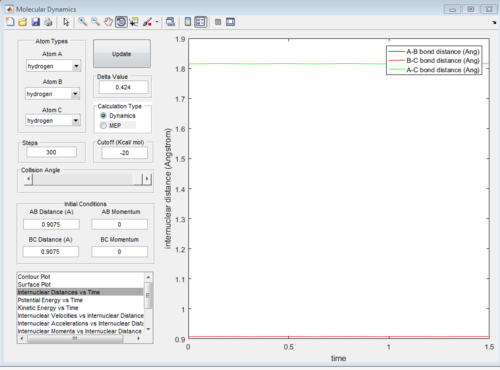
rts = 0.9075 A.This is because there is the least oscillation for this distance.
Going above/below this gives a sinusoidal function of a larger curvature for the internuclear distance vs time graph. The least oscillation gives the transition state because this is the minimum of the potential surface diagram being 'cut' at rAB=rBC. Above/below which the system will oscillate.
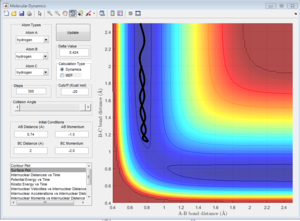
Comment on how the mep and the trajectory you just calculated differ.
mep gives a straight line trajectory that follows the floor of the valley, whereas Dynamic gives an oscillating trajectory.
Since the velocity is always reset to 0 in mep, the atom will accelerate and move in the direction of steepest descent at each time step. Thus, it will follow a curved path that corresponds to the minima of the potential surface.
For the Dynamic trajectory method, at each time step, the atom will have an initial velocity. Thus, its motion will be that of the initial velocity coupled with the acceleration due to the direction of steepest descent, which results in the oscillating path.
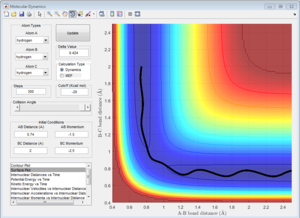
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| Condition | p1 | p2 | Trajectory | Reactive/unreactive | Description |
|---|---|---|---|---|---|
| (a) | -1.25 | -2.5 |  |
Reacts | The atoms have sufficient energy to pass through the transition state.
A bond is formed between B-C, which oscillates due to vibrations. |
| (b) | -1.5 | -2.0 |  |
Doesn't react | The atoms approach each other, but have insufficient energy to cross the transition state. |
| (c) | -1.5 | -2.5 |  |
Reacts | The atoms have sufficient energy to pass through the transition state.
A bond is formed between B-C, which oscillates due to vibrations. Compared to (a), there is vibration in the initial trajectory. This is due to the fact that AB has a higher initial momentum, meaning that it will have a higher kinetic energy for vibration. |
| (d) | -2.5 | -5.0 |  |
Reacts then returns to initial state | The atoms have sufficient energy to pass through the transition barrier, but the products recrosse the barrier and returns to the original reactants, as indicated by the reaction trajectory. |
| (e) | -2.5 | -5.2 |  |
Reacts | The atoms have sufficient energy to pass through the the transition barrier twice, resulting in the eventual formation of new bonds. |
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
- Quasi-equilibrium assumption that reactants are in equilibrium with the activated complex.[1]
- Assumes that transition states have a long enough lifetime such that Boltzmann distribution can be reached.
- Assumes that the rate of reactions can be found by focusing on the transition state. The mechanistic details of how the transition state is formed is unimportant.[1]
- Assumes that the atoms obey the laws of classical mechanics, i.e. tunneling across the barrier doesn't occur.
- Hence, it is inaccurate for light systems such as those of hydrogen, since quantum mechanical influences become important.
- Assumes that reacting molecules will pass through saddle point of the potential surface[2]
- In reality, the probability that the reaction passes through the saddle point is infinitesimally small, since it constitutes only one point on the potential energy surface. This would render the predictions of reaction rates by TST inaccurate, as some reaction trajectories need not pass through the saddle point.
- Assumes no recrossing of the activation barrier
- Hence, rate predicted by TST might be larger than that of experimental values, since recrossing of the barriers is possible, as illustrated in cases (d) and (e)
- Assumes that only 3 geometries are involved - reactants, activated complex and products
- As such the amount of energy required for the reaction would be the activation energy. However, different vibrational modes might be present for each of the species, and the actual energetics involved in the reaction is much more complicated than that of that taken into account in the transition state theory. This can be corrected by including the vibrational partition functions in the prediction of the free energy of activation besides the translational partition function.[3]
Part 2: F-H-H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
| Label | Reaction | Energetics |
|---|---|---|
| 1 | F+H2 -> H+HF | exothermic |
| 2 | H+HF -> F+H2 | endothermic |
This is because the potential energy has a smaller value when the AB (HF) distance is small, as compared to that when the BC distance is small.
Hence, the bond energy of HF is stronger than HH. This is in agreement with literature BE (H-F) = 565 kJ mol-1 BE (H-H) = 432 kJ mol-1.[4]
Locate the approximate position of the state.
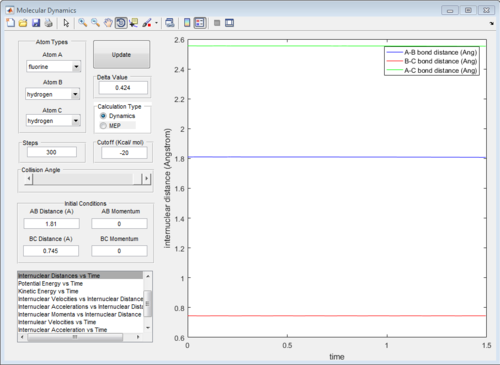
rHF = 1.81 A
rHH = 0.745 A
Report the activation energy for both reactions.
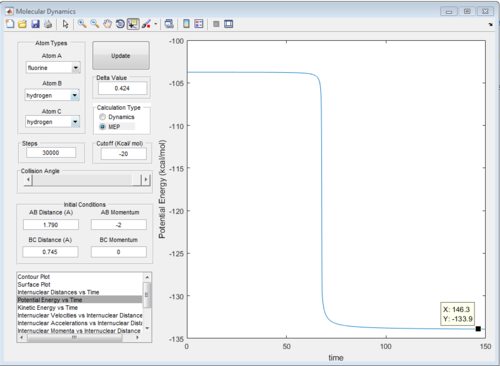
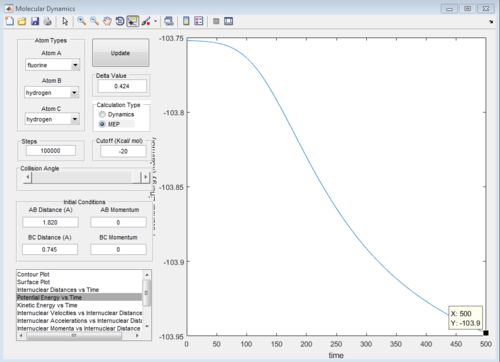
Energy of transition state = -103.3 kcal mol-1
Energy of HF and H = -133.9 kcal mol-1
Energy of H2 and F = -103.9 kcal mol-1
Thus,
Reaction 1: Ea = 0.6 kcal mol-1 (lit.[5] 1.6 kcal mol-1)
Reaction 2: Ea = 30.6 kcal mol-1
ΔrH (Reaction 1) = -30.0 kcal mol-1 (lit.[5] -31.9 kcal mol-1)
A more precise estimate of final energies
| HF and H | Energy/kcal mol-1 | Remarks |
|---|---|---|
 |
-133.9 | |
 |
-103.9 | A straight line is not observed due to the small interval of the energy.
Nonetheless, the estimate of -103.9 kcal mol-1 obtained in the section above is sufficiently accurate in comparison to this method. |
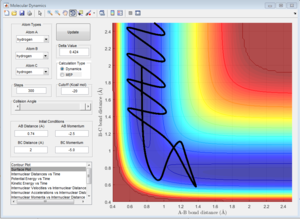
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
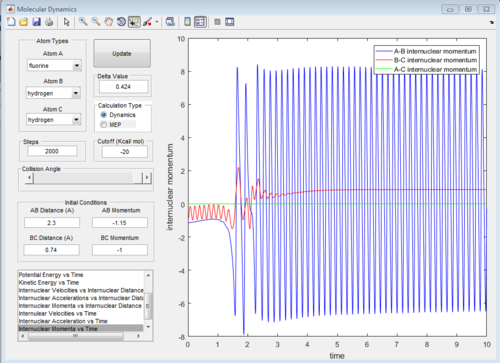
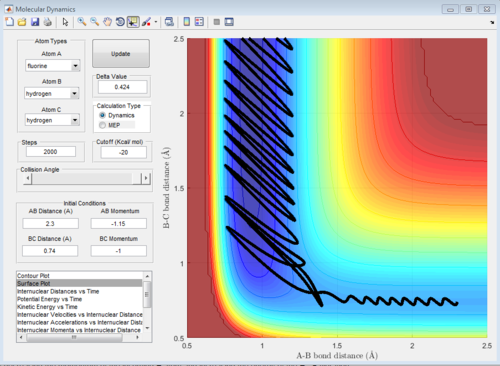
Initial conditions are:
rHF = 2.30 A, rHH = 0.74 A
pHF = -1.15, pHH = -1.00
From the internuclear momenta vs time graph, it can be seen that the momenta for HH changed from an oscillatory graph (vibration) to that of a straight line graph (translation). In contrast, that between HF changed from a straight line to an oscillatory one, representing a molecule being formed with large vibrational energy.
Due to the conservation of energy, the energy released is being stored as vibrational energy. It could be seen that the system goes from a state of low vibrational energy in HH to high vibrational energy in HF. Hence, one method to confirm this would be to measure the change in vibrational energy.
This could be done using infrared chemiluminescence, where vibrationally excited molecules emit photons in the infrared region to relax back to their ground states. Infrared chemiluminescence allows the probing of the distribution of vibrational energy in three-atom systems.[6] For this system, both the MR (measured relaxation) and AR (arrested relaxation) approach could be used to confirm the release in vibrational energy.
Also, since the reaction is exothermic, an increase in temperature would also be indicative that the reaction is successful.
Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of pHH above the activation energy (an H atom colliding with a high kinetic energy)
From the fact that KE = p2/2m, it could be noted
that the initial energy is much higher for Case 1. This shows that the energy
efficiency is better for Case 2, where a lower amount of input energy is
sufficient to achieve the desired reaction.
The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's rules state that vibrational energy is more efficient than translational energy in promoting reactions with late transition states.[7] From Hammond's postulate, this would mean endothermic reactions, since the transition state would be closer in energy to the products than the reactants. This is reflected in the section above, where Case 2 requires less initial energy for the reaction to proceed when the energy is stored in the vibrational motion of HF.
Thus, exothermic reactions (early transition states) are more energetically efficient when the reactant energy is in translational mode, whereas endothermic reactions are more energetically efficient when the reactant energy is stored in vibrational mode.
Experimentally, this would mean that the rate of exothermic reactions could be increased more efficiently by heating; whereas that of endothermic reactions could be more efficiently increased by excitation via infrared radiation.
(A great report. Nice work. Lt912 (talk) 23:19, 18 May 2017 (BST))
References
- ↑ 1.0 1.1 Laidler, K.J. and King, M.C., 1983. Development of transition-state theory. The Journal of physical chemistry, 87(15), pp.2657-2664.
- ↑ Eyring, H., 1935. The activated complex in chemical reactions. The Journal of Chemical Physics, 3(2), pp.107-115.
- ↑ Fogler, Gurmen. 2008. Transition State Theory. [ONLINE] Available at: http://www.umich.edu/~elements/03chap/html/transition/. [Accessed 4 May 2017].
- ↑ Yoder, C. 2017. Common Bond Energies. [ONLINE] Available at: http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html. [Accessed 4 May 2017].
- ↑ 5.0 5.1 Polanyi, J.C. and Schreiber, J.L., 1977. The reaction of F+ H 2→ HF+ H. A case study in reaction dynamics. Faraday Discussions of the Chemical Society, 62, pp.267-290.
- ↑ Polanyi, J. C. 1986. Nobel Lecture: Some Concepts in Reaction Dynamics". Nobelprize.org. Nobel Media AB 2014. Available at: http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1986/polanyi-lecture.html. [Accessed 5 May 2017]
- ↑ Polanyi, J. C. 1972. Concepts in reaction dynamics. Accounts of Chemical Research, 5, pp. 161−168.