MRD:jhl416
Molecular Reaction Dynamics: Applications to Triatomic systems
EXERCISE 1: H + H2 system
Dynamics from the transition state region
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
With reference to the diagram provided (Gradients at the transition state, as well as in the reactants and product regions.) in the experimental script, q1 and q2 are defined as a different set of coordinates different from the coordinates of r1 and r2. q2 is along the direction of the reaction pathway and q1 is orthogonal to the direction of the reaction pathway.
Ng611 (talk) 22:45, 7 June 2018 (BST) Good idea to use a diagram here although I think you forgot to put it in. Your definition is good though!
Both the transition structures and minima have a 0 gradient where the first derivative would both be 0, i.e. ∂Ve(q1)/∂q1 * ∂Ve(q2)/∂q2 = 0
Their second derivatives need to be used in order to distinguish between the two.
For transition structures:
As the transition state is at the maximum along the reaction pathway, the second derivative of the transition state is < 0 along the q2 direction, i.e. ∂Ve2(q2)/∂q22 < 0
While the second derivative along the q1 direction is > 0 as it is a minimum along any other directions except from the direction of the reaction pathway, i.e. ∂Ve2(q1)/∂q12 > 0.
For minima:
Minima are at minimum along all directions, including the direction of the reaction pathway. Thus, both of the second derivatives (in q1 and q2 directions) are > 0, i.e. ∂Ve2(q2)/∂q22 > 0 and ∂Ve2(q1)/∂q12 > 0.
Trajectories from r1 = r2: locating the transition state
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
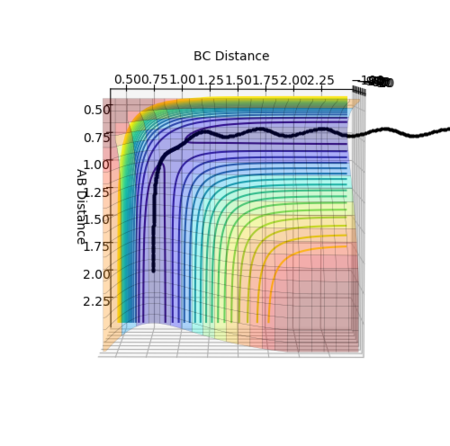
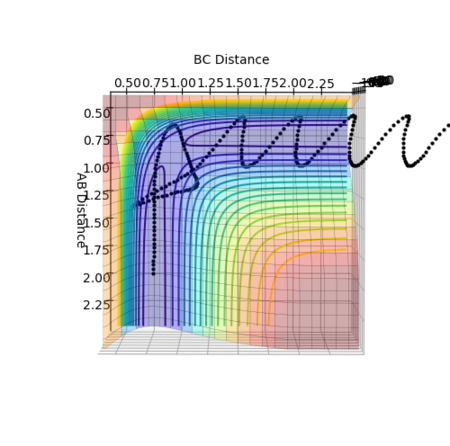
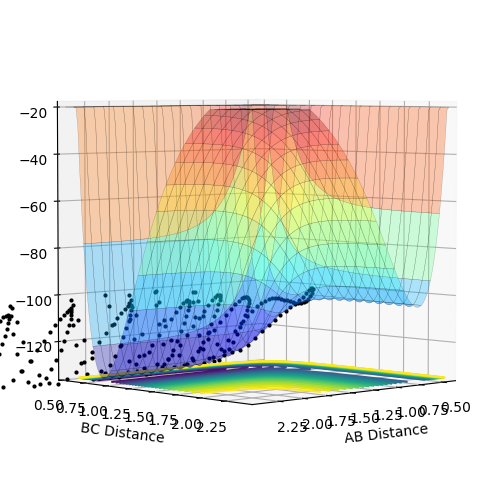
At the transition state position, there is 0 gradient. Thus, without initial momentum, the kinetic energy of the system should be 0 where there is no oscillation present. Thus, distanceA-B and distanceB-C should be constant in the system.
By testing different rts values, the best estimation of the transition state position is found to be 0.90777 Å. As seen from figure 1 above, when rts = 0.90777 Å, distanceA-B and distanceB-C are seen to be constant with no oscillation, which aligns with the above.
Calculating the reaction path
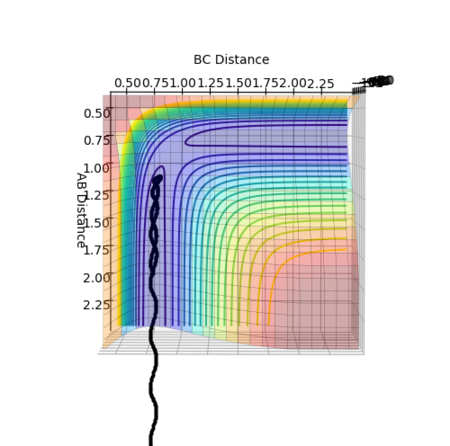
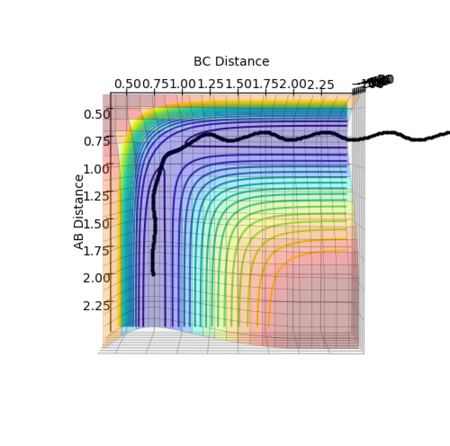
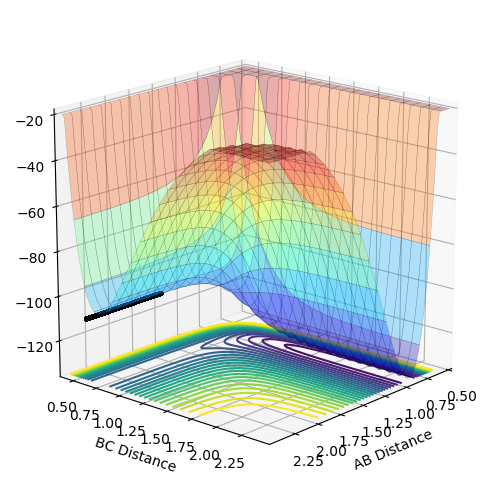
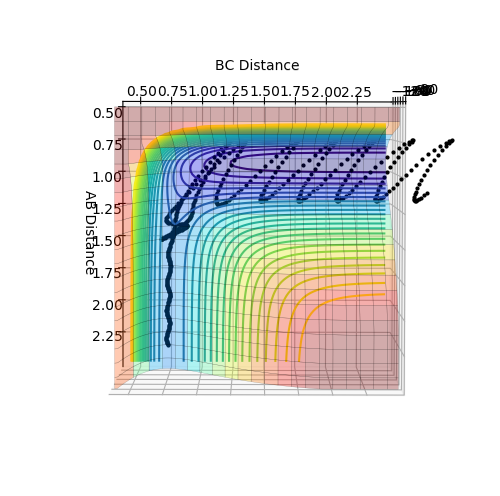
The reaction path calculated using different methods of mep and dynamics are presented below in figure 2 and 3.
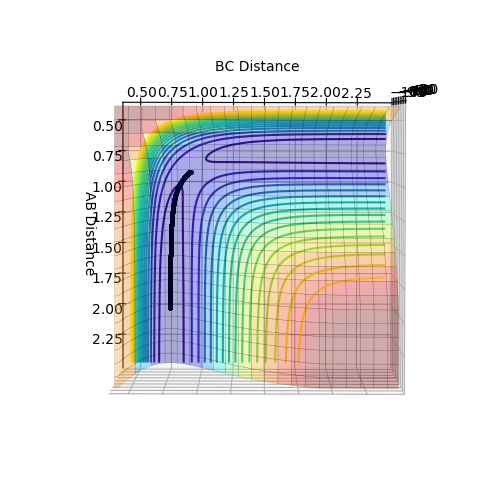
From figure 2, it is seen that the trajectory calculated using mep appears to be a straight line. This is due to the fact that mep shows an infinitely slow motion of reaction path. As velocity is set to zero at every time step, the momentum and thus kinetic energy is also zero at each time step. This results in no oscillation motion and hence a straight line of the trajectory.
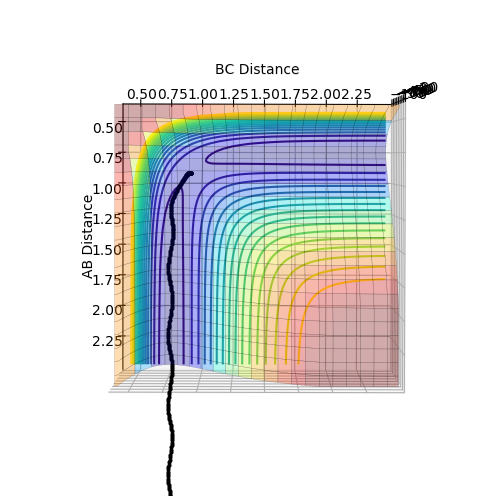
From figure 3, the trajectory appears to be more wavy when calculated using the dynamics method. This gives a more realistic picture of the motion of atoms where masses of atoms are taken into account. Thus, the oscillation motion of the atoms can then be observed.
Ng611 (talk) 22:47, 7 June 2018 (BST) Good definitions here!
Reactive and unreactive trajectories
| p1 | p2 | Reactive/Unreactive | Description | Image |
|---|---|---|---|---|
| -1.25 | -2.5 | Reactive | Along the trajectory, Hb and Hc are kept at a constant distance with no oscillation observed in the entrance channel. As Ha approaches and collision occurs, kinetic energy is enough for reaction to occur. The bond between Hb and Hc breaks and the bond between Ha and Hb is formed while Hc leaves in an opposite direction. Translational energy is converted into vibrational energy such that oscillation is observed in the exit channel between Ha and Hb. |
 |
| -1.5 | -2.0 | Unreactive | Comparing with the first momenta combination, AB momentum is lower in this momenta combination, resulting in insufficient kinetic energy to overcome the activation barrier that the trajectory is unreactive. |  |
| -1.5 | -2.5 | Reactive | Similar to the first momenta combination, this momenta combination results in a similar trajectory. The major difference is observed at the entrance channel where oscillation between Hb and Hc before the collision with Ha. This can be explained by the increased magnitude of p1 (which corresponds to BC momentum) from 1.25 to 1.5. This also means an increase in kinetic energy of atoms such that oscillation can be observed. |  |
| -2.5 | -5.0 | Unreactive | As Ha collides with the bonded Hb and Hc, the bond breaks and the the Ha-Hb bond is formed. Yet, due to the high momentum of atoms, the newly-formed bond breaks again that the Hb-Hc bond is formed again while Ha leaves in the opposite direction in a reduced speed. Trajectory is unreactive. |  |
| -2.5 | -5.2 | Reactive | Comparing with the previous case in figure 7, the magnitude of p2 (which corresponds to AB momentum) is increased from 5.0 to 5.2. Atoms behave similarly with that in figure 7. However, due to the high momentum, after the reformed Hb-Hc bond, it breaks again to form a Ha-Hb bond, leaving Hc to leave in an opposite direction. |  |
Assumptions of Transition State Theory
The following are the main assumptions of the Transition State Theory[1]
- ↑ J. W. Moore, R. G. Pearson, Kinetics and Mechanism, 1981, 166
1. Atoms behave in classical mechanics that a classical trajectory can be an accurate description of the motion.
2. There is an equilibrium between reactants and transition states.
3. Barrier recrossing does not occur.
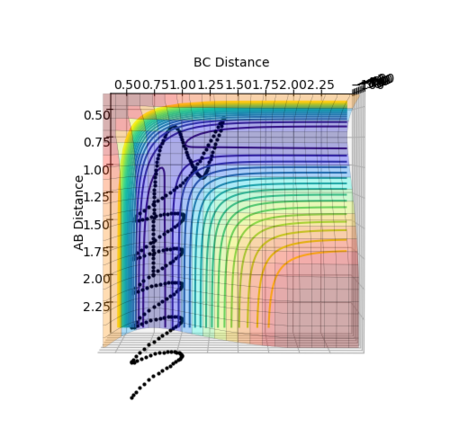
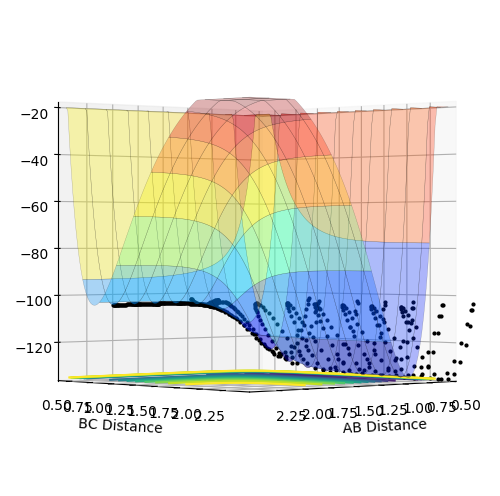
As the Transition State Theory assumes no barrier recrossing occurs, its predicted values for reaction rate is likely to be overestimated in comparison with the experimental values. Under the assumption of the Transition State Theory, all systems will continue to form products once the energy barrier is crossed for one time. However, as demonstrated in figure 7, systems do recross the barrier under certain conditions. This indicates that some of the reactive reactions predictions under the Transition State Theory might not be true. Thus, the reaction rate in reality should be lower, leading to lower experimental values in comparison with the predictions under Transition State Theory.
Ng611 (talk) 22:49, 7 June 2018 (BST) Good! Tunneling can also play a minor role although it's far less significant than barrier recrossing. Gow do you think tunelling effects will affect the reaction rate?
EXERCISE 2: F - H - H system
PES inspection
Endothermic or exothermic reactions
As shown in figure 9, the F + H2 reaction is exothermic as the energy level of the exit channel (product: H-F) is lower than that of the entrance channel (reactant: H2). An exothermic reaction indicates a negative energy change. It means more energy is released in the bond formation (formation of H-F bond) than the energy is taken in during the bond breaking (breaking of H-H bond). Thus, the bond strength of H-F is stronger than that of H-H.
As shown in figure 10, the H + HF reaction is endothermic as the energy level of the exit channel (product: H2) is higher than that of the entrance channel (reactant: H-F). An endothermic reaction indicates a positive energy change. It means more energy is taken in during the bond breaking (breaking of H-F bond) than released in the bond formation (formation of H-H bond), once again indicating the stronger bond strength of H-F than H-H.
Location of transition state
In the exothermic reaction, the activation energy is too small that it is difficult to locate the transition state. According to the Hammond postulate, the transition state resembles the structure of the reactants more than that of the products as the energy gap between the transition state and reactants is smaller than that between the transition state and products. Using this as a guide for the location, the transition state is located at where rHF = 1.8113 Å and rHH = 0.7445 Å.
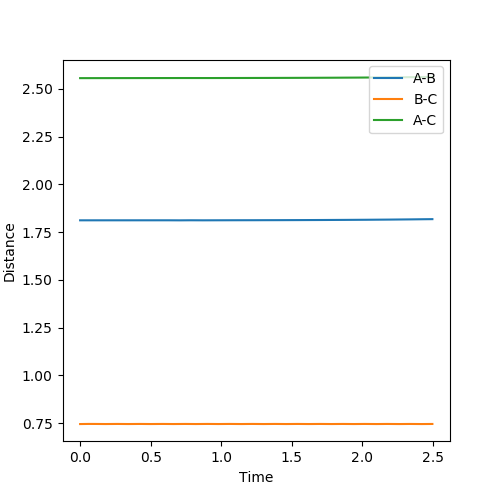
Figure 11 above shows that when rHF = 1.8113 Å and rHH = 0.7445 Å, all distances between atoms are at constant, indicating that it is the point of transition state.
Activation energy for both reactions
F + H2 reaction
By carrying out mep calculations from a structure neighbouring the transition state, figures 12 and 13 shows the energy difference between the transition state and reactants, i.e. the activation energy, for the F + H2 reaction. An activation energy of 0.243 kcal/mol.
H + HF reaction
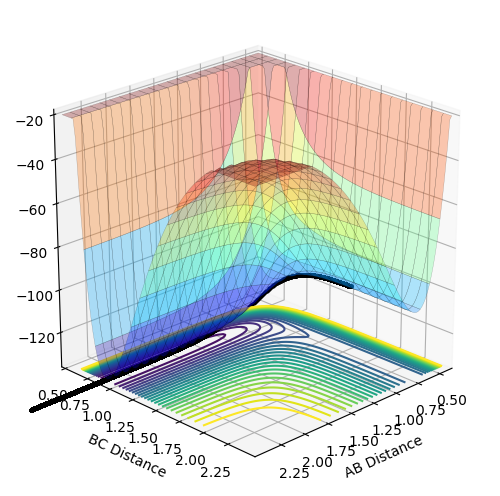
By carrying out mep calculations from a structure neighbouring the transition state, figures 14 and 15 shows the energy difference between the transition state and reactants, i.e. the activation energy, for the F + H2 reaction. An activation energy of 30.075 kcal/mol.
Ng611 (talk) 22:50, 7 June 2018 (BST) These are good estimates of the activation energy!
Reaction dynamics
Mechanism of release of reaction energy
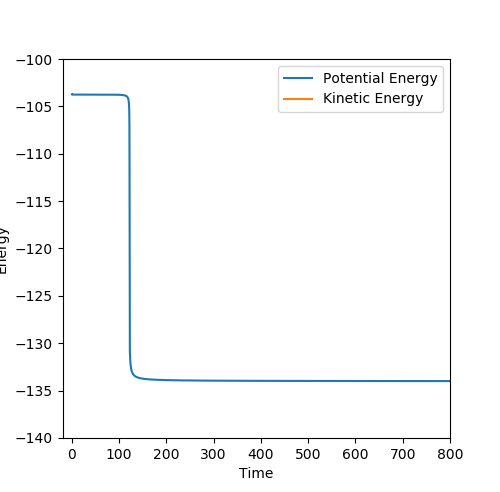
With the initial conditions of r1 = 2.3, r2 = 0.74, p1 = -2.5, p2 = -1.5, it is shown in figure 16 that the trajectory is reactive.
By looking at the animation of the reaction, it can be observed that H2 approaches F atom with little oscillation. As they collides, H-H bond breaks and H-F bond is formed. However, the H-F bonds breaks again right afterwards and H-H bond is reformed. The oscillation of H-H bond becomes stronger and collides with F atom again that H-F bond is eventually formed with stronger oscillation while H atoms leaves in an opposite direction.
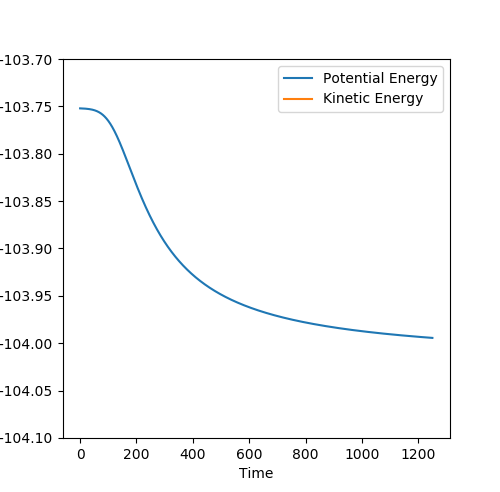
From the internuclear momenta vs time plot in figure 17, it can be seen that oscillation is initially absent between atoms A and B (i.e. atoms F and H) while present between atoms B and C (i.e. the two H atoms). Yet, after the reaction, strong oscillation is present between atoms A and B while absent between atoms B and C. In comparison, the oscillation in the initial H-H molecule is much smaller than that in the final H-F molecule. This indicates an increase of vibrational energy in the system, which is transferred from translational and potential energy.
In light of the conservation of energy, when potential energy is transferred to vibrational energy that is released in the form of heat, the temperature of the reaction will increase as a result. Thus, the mechanism of release of reaction energy can be confirmed by monitoring the change in temperature using calorimetry.
Ng611 (talk) 22:52, 7 June 2018 (BST) Calorimetry will give you an estimate of the total energy released but won't tell you about how this is distributed between translation and vibration. You need to think of another technique.
Distribution of energy
The H + HF reaction is an endothermic reaction that it has a late transition state, i.e. a late-barrier. According to Polanyi's empirical rules, vibrational energy should be more efficient than translational energy to promote this type of reactions. [1]
- ↑ Z. Zhang, Y. Zhou, D. H. Zhang, J. Phys. Chem. Lett. 2012, 3, 3416
In the following cases, initial positions are set at the bottom of the entry channel where rHF = 0.93.
In figure 18, The initial conditions applied are of high vibrational energy with low translational energy, such that the the trajectory is expected to be reactive according to Polanyi's empirical rules. The experimental result is shown to be aligned with the theory.
In figure 19, The initial conditions applied are of low vibrational energy with high translational energy, such that the the trajectory is expected to be unreactive according to Polanyi's empirical rules. The unreactive trajectory also aligns with the prediction.
However, there are also conditions found where the Polanyi's empirical rules is not obeyed.
In figure 20, The initial conditions applied are of high vibrational energy with low translational energy, such that the the trajectory is expected to be reactive according to Polanyi's empirical rules. However, the trajectory is shown to be unreactive, disagreeing with the theory.
Ng611 (talk) 22:59, 7 June 2018 (BST) Good examples! You should also add some for the F + H2 reaction though.
In figure 21, The initial conditions applied are of low vibrational energy with high translational energy, such that the the trajectory is expected to be unreactive according to Polanyi's empirical rules. Yet, a reactive trajectory is shown that it disagrees with the theory once again.
The above cases show that the Polanyi's empirical rules do not hold true at all times.
Ng611 (talk) 22:59, 7 June 2018 (BST) Very, very true, although your second counterexample doesn't actually prove anything. Basically, you're putting so much energy into the system that the atoms basically ignore the PES entirely.
Ng611 (talk) 22:53, 7 June 2018 (BST) Overall, a very good report, and there's very little to add. To improve this report further, you could consider branching out a bit more and familiarising yourself with the literature surrounding the subject. However, this is not at all mandatory and overall, your report is very good.