MRD:jh6215physcomp
Molecular reaction Dynamics - James Hale
(Fv611 (talk) 12:11, 25 May 2017 (BST) The best wiki I've seen so far. Thorough, crystal clear and to the point. Impeccable discussion, showing great understanding. Very well done!)
Exercise 1: H + H2 system
Question A
Question: What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total gradient at a minimum and a saddle point is 0 because, by definition, stationary points have 0 gradient.
A saddle point comprises of two partial derivatives and is different from a maximum or minimum because one of the double partial derivatives at this point is positive and the other is negative. However, in this case, the linear maximum and minimum that create the saddle point are diagonal to the axes. This is the case because the distance between atoms A and B and the distance between atoms B and C are used to simplify the visualization. A linear combination of atom separations would allow a numerical evaluation of the saddle point.
Transition structures are found at the highest point along the lowest energy pathway. The highest point along the lowest energy pathway is the saddle point of the plot and this is where the transition state can be found. The minima of a potential energy surface is simply the bottom valley that is created by the surface plot. Minima are different from transition structures (saddle points) because at minima both double partial derivatives are positive.
Question B
Question: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
This first guess at a solution to rts was given with both r1 and r2 equal, with no momentum. This causes the atoms to oscillate over the saddle point. Zero momentum prevents the reaction from moving along the energy pathway. When r1 and r2 are the same, within a reasonable range, they will be found at the transition structure as both outside atoms interact equally with the central atom. Using this oscillation the lowest point along the oscillatory curve was found.

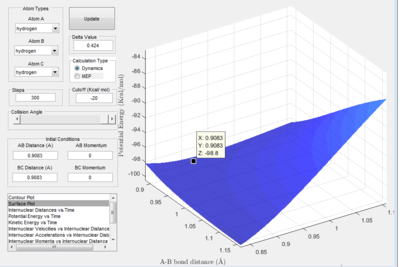

Using the previous guess, the rts was imputed as the r1 and r2 points from the lowest point along the oscillation. The lowest point of oscillation is the point at which the potential energy is least and therefore the most likely pathway for a reaction through the transition state. This resulted in a single dot appearing on the surface, showing that there were only negligible atomic vibrations. At this point the potential is poised atop of the saddle point.
The final image of this question shows the oscillation in the distances between the atoms. The constant distances between the atoms shows the system is at static equilibrium. The distance between atoms A and C is nearly constant at 1.816 A. The distance between atoms B and C, and A and B is also nearly constant at 0.9083 A. The very small oscillations are negligible in this model and so rts is 0.908 A to 3sf.
Question C
Question: Comment on how the MEP and the trajectory you just calculated differ.
The first figure is the dynamic trajectory and it shows small vibrations across the potential valley as atom A moves away from diatomic molecule B-C. The second figure is the MEP calculation, which had to be run over a much longer time frame. It shows a straight line as the atom A moves away from the diatomic molecule B-C.


The reaction occurs because the atoms start with enough potential energy to react due to their initial positions. The potential energy is then converted to kinetic energy and allows one of the atoms to escape the saddle point. The MEP just shows the minimum potential energy reaction pathway and does not account for vibrations between the bonded atoms. The dynamic trajectory accounts for the vibrations as the velocities are not reset after each time step.
To answer the question of: what would change if rts = r1 and rts = r2 + 0.01 was swapped with rts = r1 +0.01 and rts = r2? The opposite reaction would occur. In the first instance the A-B H2 molecule is formed and atom C moves away and in the second instance the B-C H2 molecule is formed and atom A moves away. This occurs because the two atoms closer together form the stronger initial bond and with no vibrational or translational energy to change this.
Question D
Question: Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
The table below gives the basic yes or no answer to whether each simulation causes the atoms to react successfully. However, the some of the reactions are more complex than this.
| p1 | p2 | Reaction | Figure | Times the Transition state is Crossed |
|---|---|---|---|---|
| -1.25 | -2.5 | yes | 1.D1 | 1 |
| -1.5 | -2.0 | no | 1.D2 | 0 |
| -1.5 | -2.5 | yes | 1.D3 | 1 |
| -2.5 | -5.0 | no | 1.D4 | 2 |
| -2.5 | -5.2 | yes | 1.D5 | 3 |
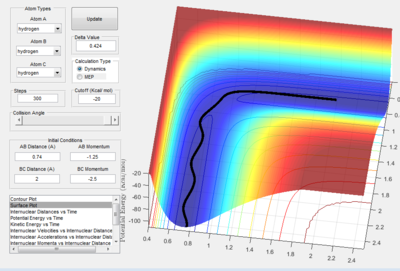
In figure 1.D1 (above) atoms A and B are initially bonded. The diatomic molecule reacts and a new molecule B-C is formed and atom A moves away.
In figure 1.D2 (above) atoms A and B are initially bonded. Atom C approaches the molecule A-B but there is not enough energy in the system for the A-B bond to be broken so no reaction occurs.
In figure 1.D3 (above) atoms A and B are initially bonded. As in figure 1.D1, atom C has enough energy to react and the diatomic molecule B-C is formed with atom A moving away.

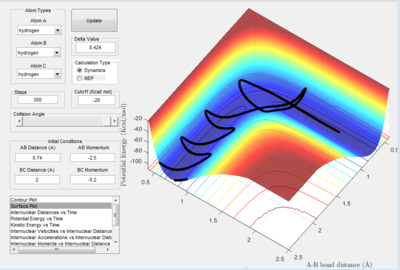
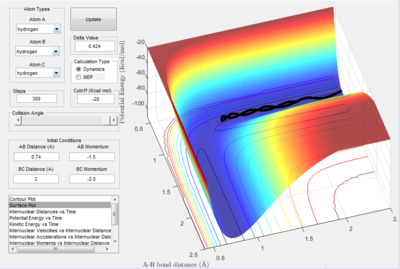
In figure 1.D4 (above) atoms A and B are initially bonded. Atom C approaches and reacts with the diatomic molecule to produce B-C. However, atom C had too much initial momentum, which causes the atoms to react again and A-B is regenerated and C moves away. Therefore, although the transition state was reached, no overall reaction occurred as the reactants are the same as the products.
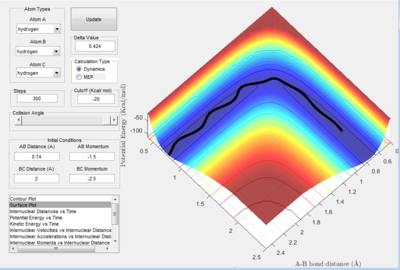
In figure 1.D5 (above) atoms A and B are initially bonded. As in figure 1.D4, atom C moves towards molecule A-B with a large momentum. In this reaction, the atoms go through the transition state 3 times. B-C is formed from the initial reaction and then A-B is regenerated. B-C is reformed in the final reaction and atom A escapes. According to results, the greater the magnitude of the total initial momentum the more consecutive times the transition state is formed before the reaction finishes.
The horizontal movement across the potential valleys is due to the large magnitude of vibrations between the atoms in molecule form. This applies to all of the figures, but 1.D4 and 1.D5 in particular. When there is a larger amount of kinetic energy in the system, translational as well as vibrational energy contributes to this, the transition state is more favoured. This can be seen in figure 1.D5 particularly, where the high magnitude oscillations cause the atoms to cross over the saddle point 3 times.
Question E
Question: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The potential surface can predict the final outcome of reactions that the transition state theory cannot. The following explanation evaluates why transition state theory is a poor approximation of the reactions in figures 1.D4 and 1.D5.
"Transition state theory is a statistical mechanical theory of chemical reaction rates that may be derived from two fundamental assumptions... The first assumption is that transition state species that originate as reactants are in local equilibrium with reactants. The second assumption is that any system passing through the transition state does so only once (before the next collision or before it is stabilized or thermalized as a reactant or product). These assumptions may be called the local-equilibrium and non-recrossing assumptions."[1]
The non-recrossing assumption, given above, is the most important in this case. In figures figures 1.D4 and 1.D5, the reaction passes through the transition state more than once. This is due to the high momenta of the atoms, which effectively models a reaction at high temperature. In this model, the reaction does not pass through the saddle point because atoms have high energy. Therefore, a higher energy transition state is formed. Due to the increased energy available to the higher energy transition state, it can decay back to the reactants or form the products. This is contrary to transition state theory, which considers the reaction completed (products formed) once the reaction has crossed the transition state region. Indeed, especially at high temperatures, some reactions may fail to reach the products after crossing the transition state. Therefore, reactions that transition state theory has predict to complete have not, thus reducing the reaction rate.[2]
Another assumption to be aware of is that transition state theory is a classical model. Therefore, quantum effects, in particular tunneling, are not accounted for. When accounting for the effect of tunneling the reaction rate increases because atoms with less energy than the activation energy are still able to react.[3]
(Fv611 (talk) 12:11, 25 May 2017 (BST) Great answer. Well done on relating to the previous examples.)
Exercise 2: F - H - H system
Question A
Question: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The energetics of the reaction can be evaluated from the potential surface of the reaction. The following two figures represent the forward reaction and backward reaction of F + H2 → F-H + H.
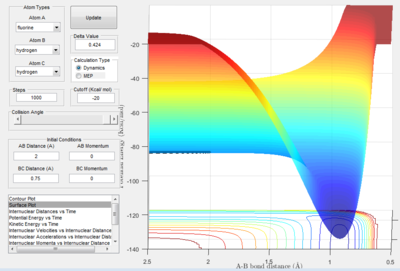

In the forward reaction, figure 2.A1 shown above) the area of potential surface where the H2 molecule is formed is of a higher energy than that of the products, H-F. Therefore the forward reaction, the formation of H-F is exothermic. The potential energy of the products is lower meaning that energy is released during this process. The backward reaction will be endothermic and this is shown in figure 2.A2 above.
Following the same logic as for figure 2.A1, the potential surface where H2 is present is higher than that of H-F. This confirms that the reaction F-H + H → F + H2 is endothermic.
The lower the potential energy surface for a diatomic molecule, the stronger the bond between the two atoms. The results conclude that the energy of the H-H bond (-104.02 kcal/mol) is higher than that of a H-F bond (-140.03 kcal/mol) and therefore the H-F bond is stronger. The bond energy values were measured using the lowest points on the respective potential energy surfaces.
Question B
Question: Locate the approximate position of the transition state.
The following images show how the saddle point of the potential energy surface was found. The transition state of H-H-F is found at the saddle point because it is the energy maximum along the lowest energy pathway. To ensure the reaction is on the lowest energy pathway, the momentum was set to 0. There will be no vibrations and the reaction will always move away from the saddle point.

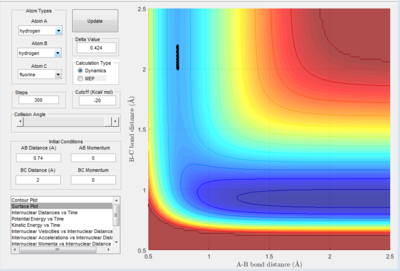
First a guess was made so the bond length of hydrogen corresponds with the lowest energy when the H-H bond is present (figure 2.B1 above). It is possible to qualitatively conclude the saddle point is closer to the H-H molecule, by looking at the surface. The reaction moves away from the saddle point towards the H-F molecule. Therefore, the next guess should be made to find a point where the reaction forms H-H, narrowing down the region which the saddle point can be in.
The next guess moves away from the saddle point to the other side (figure 2.B2 above). This process is repeated until the transition state was found.
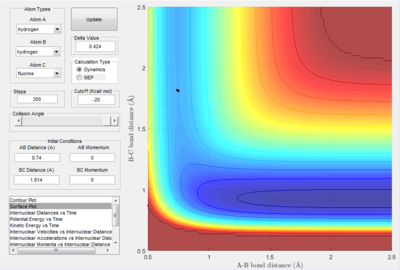
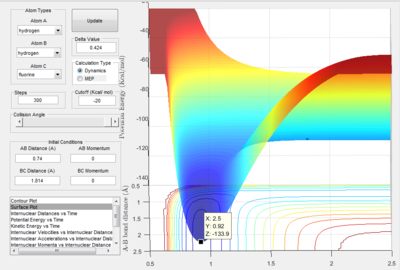
The dot in figure 2.B3 above shows that the reaction is stable atop of the saddle point. This is the transition state, the bond lengths are as follows: H-H bond is 0.740 A and the H-F bond is 1.814 A. The energy at this point is -103.75 kcal/mol, show by the time vs potential energy plot above (figure 2.B4).
Question C
Question: Report the activation energy for both reactions.
The activation energy is the difference between the energy at the saddle point (-103.75 kcal/mol) and the energy minimum of the reactants. Figures 2.C2 and 2.C4 below show the minimum energy when the reactants are H-F and H-H respectively.

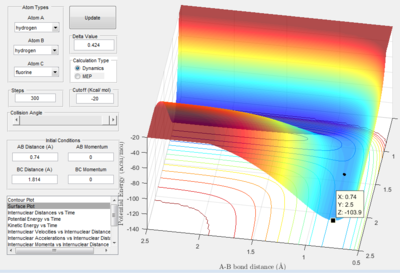
The minimum energy of H-F occurs along the lowest energy reaction pathway with the longest H-H bond. The minimum energy is -134.03 kcal/mol, therefore the activation energy for the formation of H2 from H and H-F is +30.28 kcal/mol.
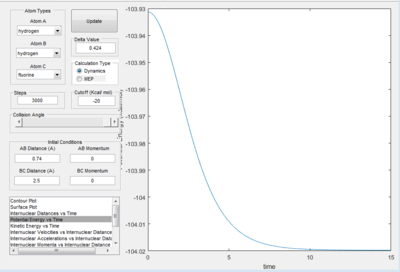
The minimum energy of H2 occurs along the lowest energy reaction pathway with the longest H-F bond. The minimum energy is -104.02 kcal/mol, therefore, the activation energy for the formation of H-F from H and H-F is +0.27 kcal/mol.
Question D
Question: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A successful reaction for the formation of F-H is shown below in figure 2.E1. Having established in question 2A that the reaction is exothermic, it is important to know how the energy is conserved.
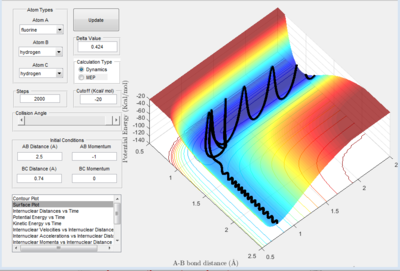

Figure 2.E2 shows the internuclear momenta vs time plot of the successful H-F formation reaction. Both figures show, that the amplitude of the vibrations has increased significantly, indicating an increase in vibrational energy. Translational energy is also likely to have increased but it is not obvious from either figure as the vibrational peaks occur at a similar frequency in figure 2.D2. The energy released will not be converted to rotational energy as the atoms collide at exactly 180 degrees. Therefore, the energy released from this exothermic reaction is primarily conserved by being converted to vibrational energy.
An increase in vibrational energy can be detected experimentally using an IR spectrometer, the intensity and the frequency of specific vibrations can be found using this technique. Calorimetry can also be used to measure the thermal energy generated by an experimental reaction.
Question E
Question: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
"Polanyi rules, which state that vibrational energy is more efficient in promoting a late-barrier reaction (that is, a transition state resembling the products) than translational energy, whereas the reverse is true for an early barrier reaction."[4] An exothermic reaction has an early transition state in the reaction process (the formation of H-F) and an endothermic reaction has a late transition state (the formation of H2). Therefore, for the formation of H2 from H-F and H, translational energy is more efficient than vibrational energy at promoting the reaction. The opposite is the case for the formation of H-F.
The effect of greater vibrational energy in a reaction weakens the initial bond and therefore helps the breaking of the bond,which promotes the reaction. In an endothermic reaction, vibrational energy has a greater effect on reaction efficiency because at the transition state the bond of the reactants is closer to being broken than in an exothermic reaction.[5]
The figures below represent 4 reactions where Polyani's rules have shown to be true.
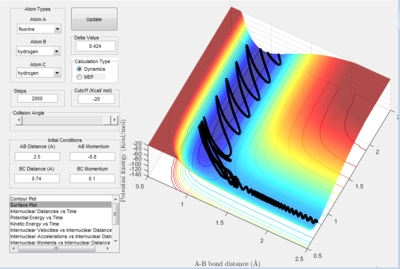



However, is difficult to confirm the Polyani rules from this model because it is only representative of one individual reaction each time different parameters are applied. All of the reactions are also only collisions at 180 degrees, which further limits the strength of these results. To measure investigate the rules on a macroscopic scale, a reaction could be irradiated with IR radiation and the effect on the reaction could be monitored.
(Fv611 (talk) 12:11, 25 May 2017 (BST) Great discussion.)
References
- ↑ D. Truhlar, B. Garrett, Ann. Rev. Phys. Chem., 1984, 35, 159-89, http://www.annualreviews.org/doi/pdf/10.1146/annurev.pc.35.100184.001111
- ↑ J. Pineda, S. Schwartz, Phil. Trans. R. Soc., 2006, 361, 1433–1438, doi:10.1098/rstb.2006.1877
- ↑ P. Atkins, J. de Paula, “Physical Chemistry”, Oxford University Press, 8th edition, 1990, 869-892
- ↑ Z. Zhang, Y. Zhou, D. Zhang, G. Czako, J. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416-3419, dx.doi.org/10.1021/jz301649w
- ↑ R. Silbey, R. Alberty, M. Bawendi, “Physical Chemistry”, John Wiley & Sons, 4th edition, 2005, 665-701
