MRD:jef15

Exercise 1: H + H₂ system

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The total gradient of the potential energy surface is zero at both minima and the transition structure (given by a saddle point). The second partial derivatives are used to distinguish between the two. The second derivative test discriminant is given by

D = f_xx + f_yy - f_xy²

At a minimum, D>0 and f_xx>0; at a saddle point, D<0.

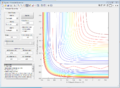
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

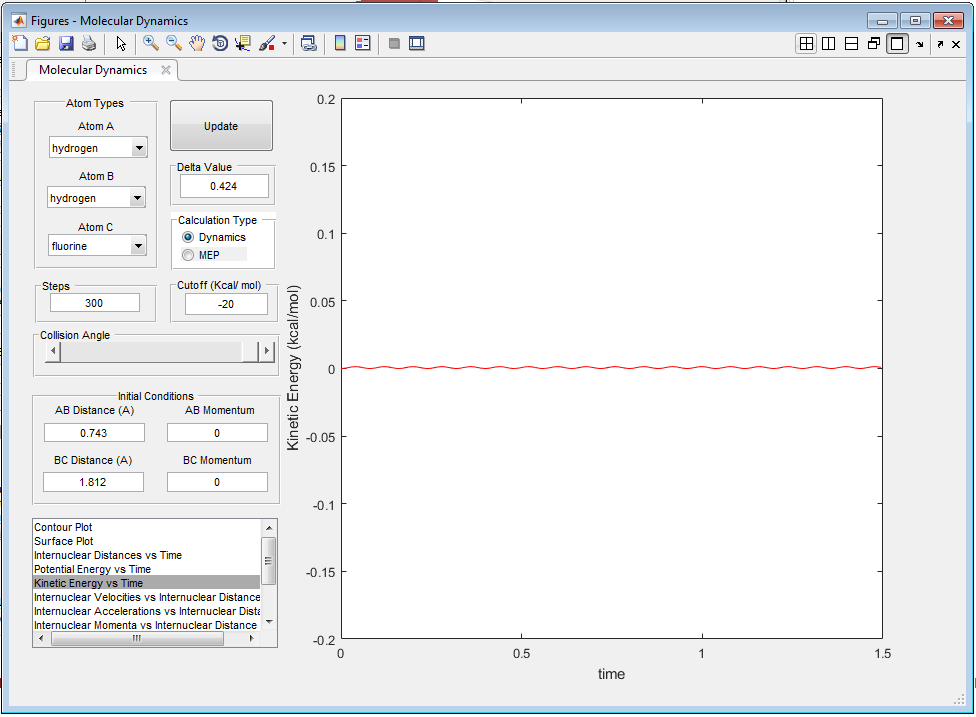
The transition state is found at approximately r_ts=0.908 Å, shown in Figure 1. This is the internuclear distance at which the oscillations are close to non-existent, and where only potential energy contributes to the state. Although some small oscillations are still observed at this point, they are insignificant.

Figure 1: Plot of Internuclear Distance vs. Time for r_ts=0.908

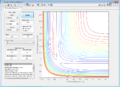
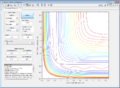
Comment on how the mep and the trajectory you just calculated differ.

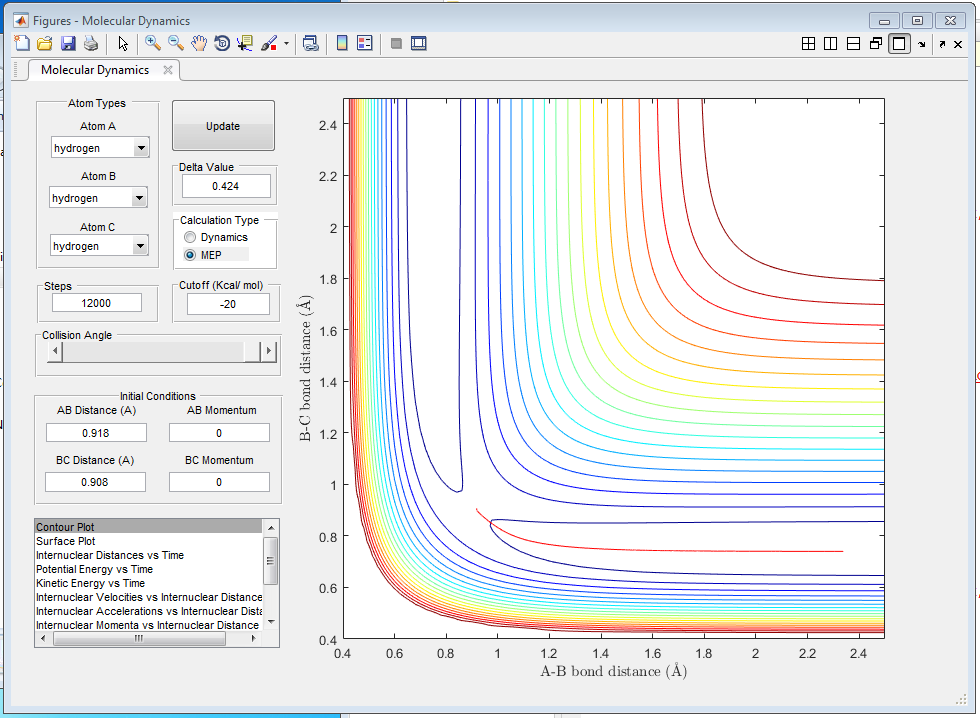
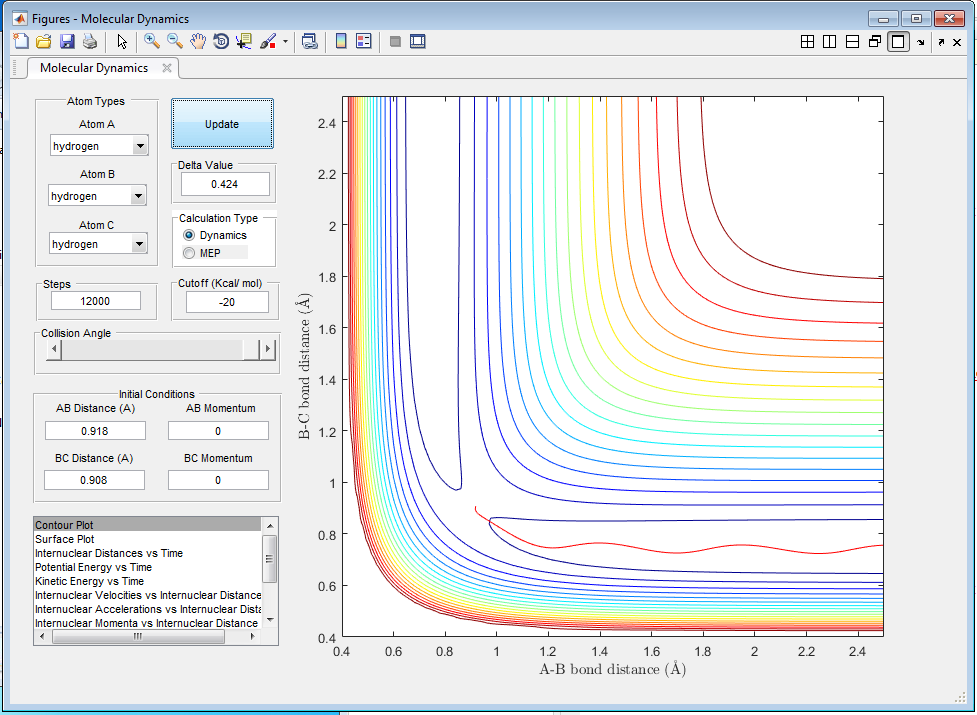
The MEP (figure 2) shows the path of lowest energy, disregarding the oscillations within the molecule. The dynamic trajectory (figure 3) shows a more realistic path, in which the particle moves up and down the "valley" as it oscillates.

Figure 2: Minimum Energy Path

Figure 3: Dynamic Trajectory

What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead?

If the initial conditions are changed in such a manner, the resulting MEP and trajectory does not lead to products but reactants.

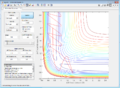
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

Conditions	p1	p2	Trajectory type
1	-1.25	-2.5	Reactive
2	-1.5	-2.0	Unreactive
3	-1.5	-2.5	Reactive
4	-2.5	-5.0	Unreactive
5	-2.5	-5.2	Reactive

• 
  Figure 4: Conditions 1
• 
  Figure 5: Conditions 2
• 
  Figure 6: Conditions 3
• 
  Figure 7: Conditions 4
• 
  Figure 8: Conditions 5

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

1. The theory also assumes that the nuclei behave according to Newtonian mechanics. So it is assumed that unless the collision takes place with enough energy, the reaction does not occur. However, quantum mechanics tells us that for a barrier with finite energy there is a possibility of the particles tunneling, and thereby reacting.

2. Another assumption of the theory is that the reaction passes through the saddle point at the lowest energy. This is fine for low temperatures but fails at higher temperatures and the molecules pass through higher energy transition states.

The experimental values for the rate could be either greater or lower than the predicted rate. The effect of tunneling could increase the rate, if the length of the barrier is short enough to make the effect significant. If the molecules pass through higher energy states, the rate of reaction will be reduced since the the energy barrier will be greater. The competition between these factors makes it difficult to state whether the prediction over- or under-shoots.

Exercise 2: F-H-H system

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F + H₂ is an exothermic reaction, which can be seen by the shape of the potential energy surface. When the product is formed, i.e. the A-B bond length is increasing, the curve is of a lower potential energy. The opposite for FH + H, so it is endothermic. Therefore, the H-F bond must be stronger than the H-H bond which makes sense since there is more ionic character in the bond.

Figure 9: H₂ + F potential energy surface

Figure 10:FH + H potential energy surface

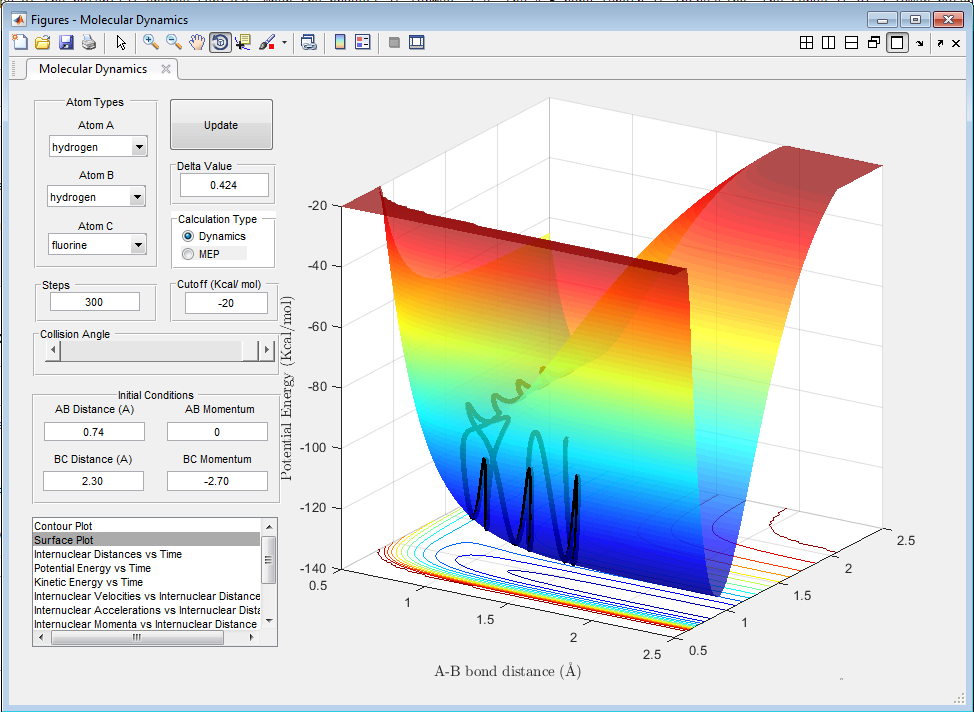
Locate the approximate position of the transition state.

The Hammond postulate tells us that the transition state will resemble H₂ + F due to the reaction being exothermic in the H₂ + F → HF + H direction, and therefore having an early transition state. The transition state is found at with H-H and H-F bond lengths of approximately 0.743 Å and 1.813 Å, respectively. The point was found approximately on the potential energy surface and the lengths were altered to give the minimum kinetic energy, oscillating at approximately zero.

Figure 11: Kinetic energy variation with time at approximate transition state bond lengths for H₂ + F system.

Report the activation energy for both reactions.

The activation energy is found by comparing the potential energy of the transition state (-103.75 kcal/mol) to the potential energy of the reactant and product states. The potential energy of the H₂ + F reactant state is -104.02 kcal/mol, giving the activation energy as 0.37 kcal/mol. The potential energy of the reactants in the FH + H reaction is -134.03 kcal/mol, so the activation energy is 30.28 kcal/mol.

Reaction Dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

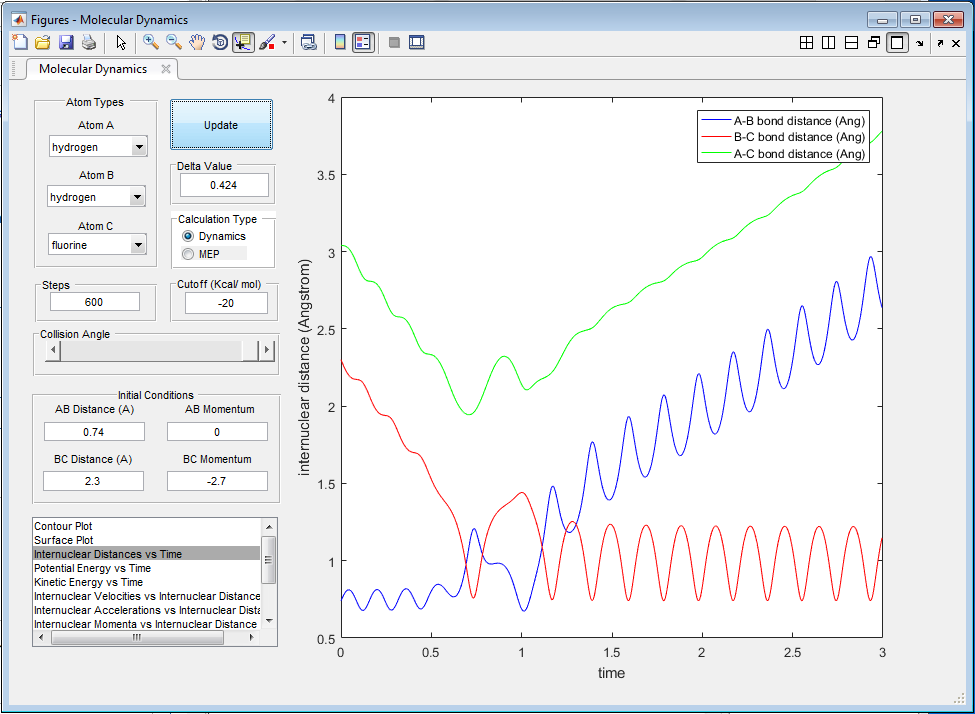
The potential energy released in the reaction is converted into kinetic energy, causing the HF molecule to vibrate with greater velocity and amplitude, despite having a larger reduced mass (figures 12 and 13). This can be confirmed by measuring the heat given out by the reaction via calorimetry.

Figure 12: Internuclear Distances vs Time

Figure 13: Internuclear Velocities vs Time

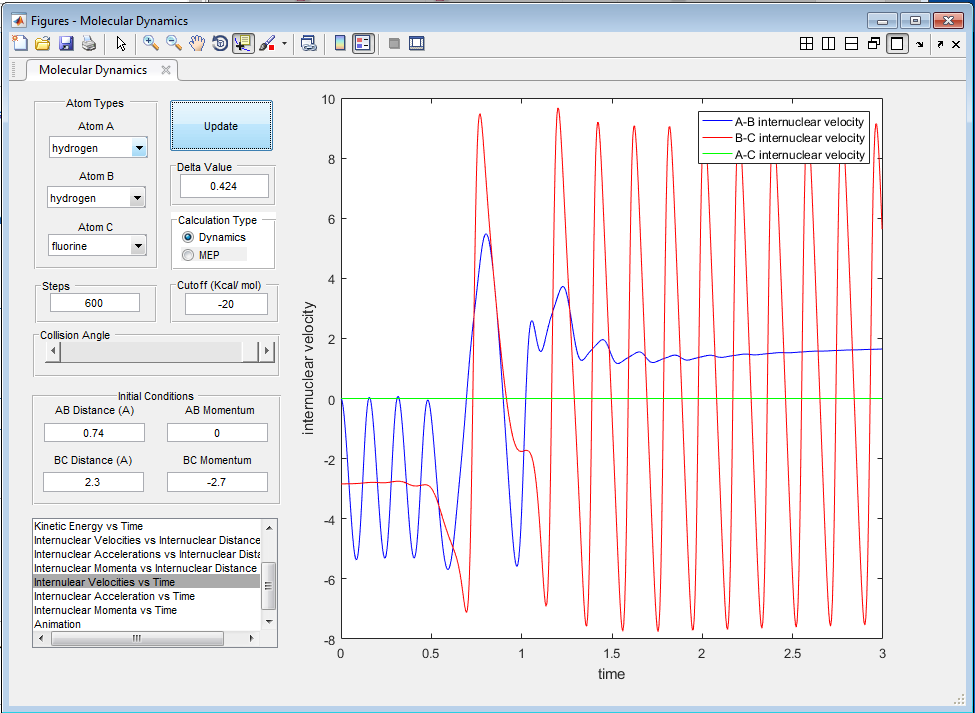
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that translational excitation (high kinetic energy) is more effective for a reaction with an early transition state (i.e. exothermic) and results in vibrationally excited product molecules. They also state that vibrational excitation is more effective for late transition state reactions (i.e. endothermic) and results in translational excitation.