MRD:jc8717
Exercise 1
Finding the Transition State
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
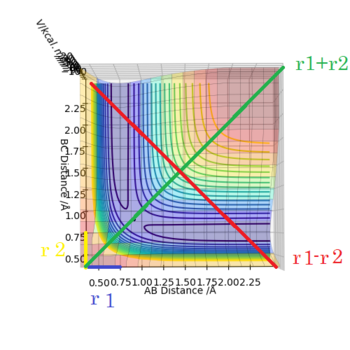
On a potential energy surface diagram, which is defined mathematically as a two-variable function generically Φ(x,y), the TS can be identified as a saddle point, that is, a point in which ∂(Φ)/∂(x) = ∂(Φ)/∂(y) = 0 and ∂(Φ)/∂2(x) > 0 , ∂(Φ)/∂2(y) < 0 or viceversa.
The potential energy surface is not necessarily a two-variable function. For example for methane, you have 5 atoms, each of them having three coordinates... How many dimensions would that PES have as a function? How many of them are the interesting 'internal' coordinates? Fdp18 (talk) 10:26, 27 May 2019 (BST)
The picture on the left is basically a contour plot (i.e. the projection along the z axis). Its much easier to interpret if you just plot it as contour in the first place. Fdp18 (talk) 10:30, 27 May 2019 (BST)
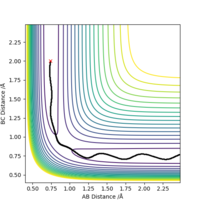
Observing this surface energy plot it can be seen that the TS is actually the saddle point that defined by ∂(V)/∂(r1+r2) = ∂(V)/∂(r1-r2) = 0 and ∂(V)/∂2(r2+r1) > 0 , ∂(V)/∂2(r1-r2) < 0.
I like that redefinition of the directions, it shows that you actually understand what this is about. Fdp18 (talk) 10:31, 27 May 2019 (BST)
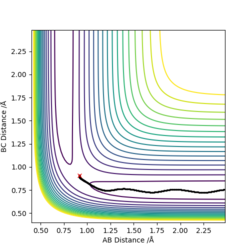
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
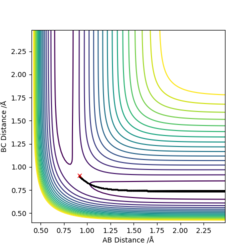
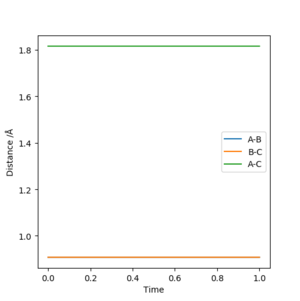
By iterating for several different values of r, TS r was found to be r1=r2=0.90775 Å, with the force along AB and along BC ≈ 0.
The Internuclear Distances vs. Time plot, shows all internuclear distances to be constant, confirming that we have found the coordinates of the Transition State.
Reaction Trajectories
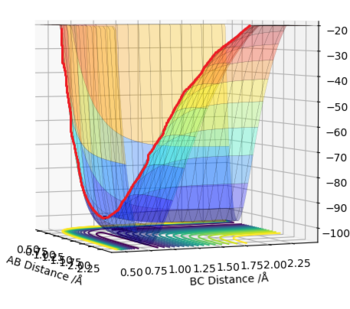
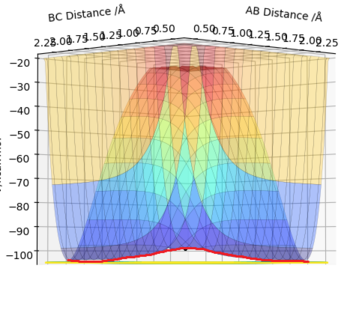
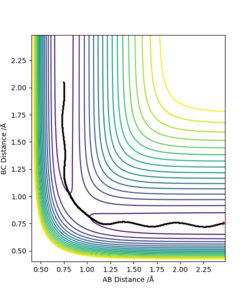
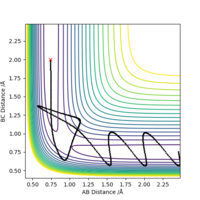
Due to the symmetrical nature of the Potential Surface, the TS is found at r1=r2=req. A small displacement from this metastable equilibrium leads to the reaction taking place. Several trajectories will now be calculated, starting with a minimum energy potential (mep) and a regular dynamic trajectory, both resulting from slightly displacing r1. Then, a trajectory resulting from a displacing r2. Lastly, inverting the momenta of a system that has reached the products. Comment on how the mep and the trajectory you just calculated differ.
| Title | Image | Description | |
|---|---|---|---|
| MEP |  |
The mep for this triatomic system, beginning from r1 slightly displaced from the TS. | |
| Dynamics Trajectory |  |
Similarly as for the mep, by using the dynamic calculation type. | |
| Dynamics Trajectory (displacing r2 from equilibrium) |  |
As above, only r2 is slightly displaced in this case, which makes the reaction proceed in the other direction | |
| Trajectory inverting momentum from products |  |
Taking the end coordinates of the H-H + H -> H + H-H reaction and inverting the momentum, the system is made to undergo the reverse reaction. |
The mep follows the ridge at the bottom of the potential energy well, with no oscillation in neither A-B or B-C distances, as there is no momentum in the mep. The Dynamic trajectory shows oscillation, and contrary to the mep total energy stays constant as the potential energy is transformed into kinetic energy.
Reactive and Unreactive Trajectories
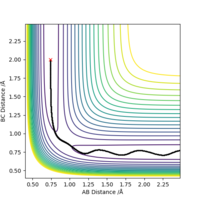
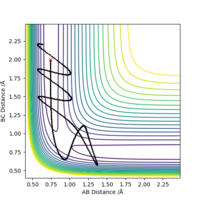
Trajectories that lead to reactions taking place are termed reactive, on the contrary, those that do not are termed unreactive. Initially, it would be assumed this is determined simply by if the trajectory has enough energy to proceed to products. The table below shows several trajectories that have been computed.
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 kcal/mol | Y | The BC distance steadily decreases as C approaches B, reaching the TS, past the TS, the BC distance oscillates slightly while AB distance increases as A and the new molecule move away from eachother. | 
|
| -1.5 | -2.0 | -100.643 kcal/mol | N | The BC distance decreases (approach of C), however, the AB distance is strongly oscillating (vibrational motion). The system does not reach the TS due to this and returns to the reactants. | 
|
| -1.5 | -2.5 | -98.956 kcal/mol | Y | The BC distance decreases (approach of C) and AB oscillates. The system passes through the transition state and to the products, with A and B-C getting further apart and the B-C distance oscillating. | 
|
| -2.5 | -5.0 | -84.956 kcal/mol | N | The BC distance decreases (approach of C), the reaction makes it past the transition state, however it crosses back into the reactants side, with A-B oscillating (due to A-B having absorbed the energy into vibrational energy.) | 
|
| -2.5 | -5.2 | -83.416 kcal/mol | Y | As above, the system crosses back into the reactants, only it crosses again into the products, with the product B-C vibrating strongly. | 
|
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
What can be concluded from this set of trajectories is a system being higher in KE (with more that enough energy to reach the transition state) does not imply that the trajectory will eventually lead to the products side.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition State Theory (and the calculations that are carried out here) assumes reactions work according to Classical Mechanics, which at the scale of chemical reactions, is inaccurate due to orbital interactions (which arise from quantum mechanics) being the basis of chemical reactions. TS theory assumes simple nuclear collisions and electrons (or for that matter, electron tunneling) are not considered, electron mass or interactions are not accounted for due to electrons being much smaller the nucleus.
That is not what is meant by 'classical molecular dynamics', although the expression is admittedly misleading. It means that the trajectory is obtained by propagating the nuclei according to classical newtonian mechanics. However, the potential in which these movements occur still has to obey the laws of quantum mechanics, even without explicit wavefunction. Electron tunneling (like, Zener tunneling) can be safely ignored here. I would strongly recommend to revise the theory behind all this. Fdp18 (talk) 10:39, 27 May 2019 (BST)
This can indeed be a tricky concept, so I'll add a bit of detail to the previous comment. The key is to think about the Born-Oppenheimer approximation where by electronic and nuclear motion are separate: nuclei move as if the electrons are always equilibrated to their current position, and electrons instantaneously equilibrate to the position of nuclei at each moment in time. (Since the electrons follow the nuclei, when we talk about motion of the nuclei we are talking about the nucleus with the cohort of electrons, i.e. the atoms).
The forces acting on the nuclei, the PES of this experiment, depend on the energy of the electrons and how that energy changes by changing the positions of the nuclei. The energy of the electrons themselves must always be calculated by quantum mechanics. Like in this experiments, one might not treat the electrons explicitly and just define a function for the PES. Importantly, this does not mean you are ignoring the electrons, it means you are approximating the quantum mechanical energy of the electrons by some function you believe is realistic. This does not prevent you from describing chemical reactions or molecular interactions (you don't explicitly "see" the orbitals, but their effect is "felt" through the energy in the PES).
For the nuclei, once you have the PES, you can decide to treat their motion by quantum mechanics (allowing for tunneling and vibrational energy levels) or classically (like in this experiment). João (talk)
Exercise 2
PES analysis
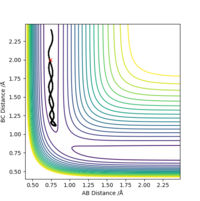
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
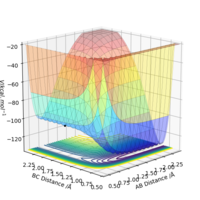
F + H2 -> F-H + H Exothermic
F-H + H -> F + H2 Endothermic
This implies that the F-H bond is much stronger than the H-H and much difficult to break (needing an input of energy (+ΔG, thus endothermic) to do so).
Locate the approximate position of the transition state
By the same method used for the H--H--H potential energy surface, with the intuition (from Hammond's postulate) that the TS is going to be closer to the H-H + F side, the TS coordinates are:
r1 = 0.74485 Å
r2 = 1.81050 Å
Report the activation energy for both reactions
F + H2 -> F-H + H Activation E: 0.096 kcal/mol
F-H + H -> F + H2 Activation E: 29.82 kcal/mol
Calculated by slight displacement from the TS in an mep trajectory.
I think your MEP for F + H2 -> F-H + H might not have gone to completion. Maybe provide a picture to support your discussion / show what you did? Fdp18 (talk) 10:43, 27 May 2019 (BST)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
Initially, the H2 bond vibrates,then the bond breaks and the H-F bond forms and vibrates very strongly, some of the energy trapped in the H2 bond has gone into the H-F bond vibration. As mentioned before the reaction is exothermic and it would liberate heat.
Additionally, several calculations starting from coordinates r1=0.74 Å, on the F + H2 side, with low approaching F momentum (p2=-0.5) and a range of H-H momenta from -3 to +3 lead to no reactive trajectories, while increasing p2 to -0.8 while overall lowering the total energy of the system lead to trajectories being reactive.
For a H-F + H reaction, starting at that the H-F end of the PES(r1=2.4 Å, r2=0.9 Å);
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Conditions in which momentum in the H-F bond is small and momentum of the approaching H is large lead to unreactive trajectories. Conversely, the opposite is true for high H-F momentum and low approaching H momentum, leading to reactive trajectories. As it was seen before, the TS is similar to the F + H2 side, meaning that it is an early TS for F + H2 -> F-H + H and a late TS for F-H + H -> F + H2, which would lead to their opposite behaviours.
You should get in the habit of proper referencing, especially your theory like Hammonds postulate or TST. Fdp18 (talk) 10:40, 27 May 2019 (BST)