MRD:hz4315
Molecular Reaction Dynamics
Exercise 1: H + H2 system
Q(1)
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
A:
Inspection of the potential energy surface curvature shows a maximum point between two minimum points, all of which are stationary points with a gradient of zero. This can be confirmed by finding the first derivative of the curve where the rate of change is zero. Transition structures always occur at the maximum point hence, it is clear that the transition state lies at this point. To distinguish between the transition state and the minima, the second derivative can be calculated which will be negative and positive for the maxima and minima respectively.[1]
Q(2)
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
A:
The approximate transition state position (r(ts)), which was found by examining the surface plot, can then be confirmed by analysing the internuclear distance vs time plot, specifically the point of intersection between the maxima and minima. The corresponding value for r(ts) is shown in the table below:
| r1 | r2 | r(ts) |
|---|---|---|
| 1.20 | 1.20 | 0.908 |
| 0.91 | 0.91 | 0.908 |
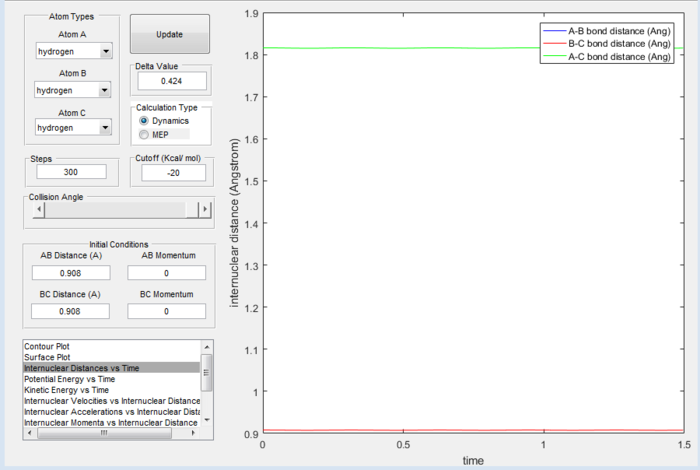
By definition, a transition state is a point where the internuclear distance between all bonds remains constant and therefore does not oscillate. As shown by figure 1, the internuclear distance does not oscillate at 0.908Å hence, this is the transition state position.
Q(3)
Comment on how the mep and the trajectory you just calculated differ.
A:
There are two distinct differences between the mep and dynamic calculations. The mep calculation only spans the distance occupied by the transition state whereas the dynamic calculation spans more of the reaction pathway. Furthermore, the dynamic calculation incorporates mass hence, the resulting reaction pathway line exhibits oscillation. In contrast, mep calculations do not use mass and therefore no oscillation is witnessed.
Q(4)
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
A:
For the initial positions r1 = 0.74 and r2 = 2.0, the following results were obtained:
The effect of changing momentum on whether a trajectory is reactive or unreactive:
| p1 | p2 | Trajectory | Figure No. |
|---|---|---|---|
| -1.25 | -2.5 | Reactive | 2 |
| -1.5 | -2.0 | Unreactive | 3 |
| -1.5 | -2.5 | Reactive | 4 |
| -2.5 | -5.0 | Unreactive | 5 |
| -2.5 | -5.2 | Reactive | 6 |
Figure 2
The plot below shows the reactive trajectory associated with the set parameters for Figure 2. The trajectory line indicates that the A-B bond distance decreases as atom Ha approaches molecule Hb-Hc whilst the B-C bond distance stays relatively constant. The line continues through the transition state where r(A-B)=r(B-C) after which r(A-B) reaches a minimum and oscillates which indicates that the Ha-Hb bond has formed whilst r(B-C) simultaneously increases, showing that the Hb-Hc bond has broken and Hc now exists as a separate atom.

Figure 3
The plot below shows the unreactive trajectory associated with the set parameters for Figure 3. The trajectory line shows r(A-B) decreasing as Ha approaches Hb-Hc. However, since Ha does not possess sufficient momentum to overcome the activation barrier, the trajectory never reaches the transition state. The plot reflects this as it shows r(A-B) returning to a larger distance before the transition state is reached. r(B-C) oscillates due to vibrational energy within the molecule.

Figure 4
The plot below shows the reactive trajectory associated with the set parameters for Figure 4. The reaction trajectory shows a successful reaction where Ha possesses enough momentum to overcome the activation barrier when approaching Hb-Hc hence, it passes through the transition state. The reaction then proceeds to form the molecule Ha-Hb.

Figure 5
The plot below shows the unreactive trajectory associated with the set parameters for Figure 5. The reaction trajectory for these parameters initially shows that Ha approaches Hb-Hc with sufficient momentum to overcome the activation barrier and reach the transition state. However, instead of proceeding to the products, the reaction trajectory returns back to the reactants with molecule Hb-Hc possessing a large amount of vibrational energy.

Figure 6
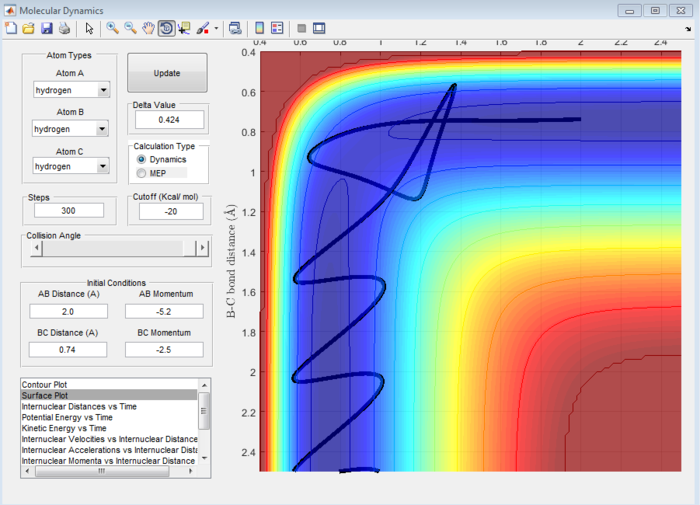
The plot below shows the reactive trajectory associated with the set parameters for Figure 6. The reaction trajectory indicates that Ha has sufficient momentum to overcome the activation barrier however, upon reaching the transition state, the trajectory is driven back towards the reactants which is illustrated by r(B-C) decreasing and r(A-B) increasing. r(A-B) reaches a maximum value before decreasing and oscillating, indicating the formation of Ha-Hb. This trajectory suggests that the reaction has taken an alternative reaction pathway which avoids the 'saddle point' on the potential energy plot associated with the transition states to yield the desired products.
Q(5)
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
A:
One assumption of the Transition State Theory is that the reactants and activated transition states are in quasi-equilibrium. Quasi-equilibrium involves the molecular driving forces which would alter the state of the system being very small, resulting in an internal equilibrium being reached. Deviations from this system are very small. In addition to this, according to the Classical Transition State Theory, providing an atom possesses sufficient momentum to overcome the activation barrier, upon collision with another molecule it will react, yielding products. However, since the theory does not account for potential quantum mechanical effects, the resulting reaction rates will be lower than expected. Quantum mechanical contribution can provide alternative reaction pathways through the introduction of tunneling. This can occur when the atom and molecule do not have the required energy to overcome the activation barrier however, due to the wave like properties of the particles, they can 'tunnel' through the barrier instead. As a result, quantum mechanics allows certain reactions to avoid the classical 'saddle point' on the potential energy surface plots associated with the transition state and instead take up an alternative reaction pathway through the barrier.[2]
Exercise 2: F - H - H system
Q(6)
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
A:
Key points:
- H-F Bond Energy = 565 KJ/Mol[3]
- H-H Bond Energy = 432 KJ/Mol[3]
- H-F is a stronger bond than H-H
- ΔE = E(bonds broken)-E(bonds formed)
F + H2 --> ΔE = 432 - 565 = -133 KJ/Mol THEREFORE EXOTHERMIC
H + H-F --> ΔE = 565 - 432 = 133 KJ/Mol THEREFORE ENDOTHERMIC
Q(7)
Locate the approximate position of the transition state.
A:
To determine the position of the transition state, the radii at which the total energy of the system is stationary (ie. the gradient is zero) were found. The location of these radii is such that the net force acting upon them is zero and plotting the internuclear distance against time results in a constant internuclear separation which does not oscillate. The internuclear separations are shown below and the associated plot against time can be seen in figure 7:
- r(H-H) = 0.74Å
- r(H-F) = 1.815Å

Q(8)
Report the activation energy for both reactions.
A:
In order to determine the activation energy for both reactions, chemical intuition and trial and error were used to find a suitable reaction trajectory. The activation energy was then equal to the difference in energy between that of the reactants and the transition state. The activation energy values obtained were done without mathematical analysis therefore, all energy values involved would actually have a +/- value.
Reaction 1: F + H2 --> HF + H
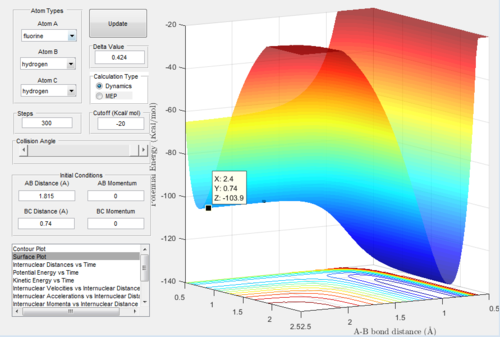
- Ea = -103.7 - (-103.9) = 0.2 KCal/Mol
The energy values used for this calculation were obtained from Figure 8 (reactants) and Figure 9 (transition state) as shown below:

Reaction 2: H + HF --> F + H2
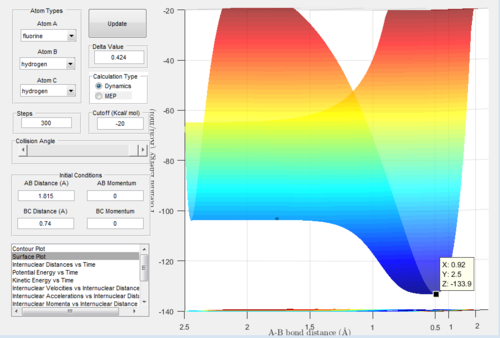
- Ea = -103.7 - (-133.9) = 30.2 KCal/Mol
The energy values used for this calculation were obtained from Figure 10 (reactants) and Figure 9 (transition state) as shown below:

Q(9)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A:
According to the Law of Conservation of Energy, the total energy of an isolated system must be conserved as energy is neither created nor destroyed, just converted from one form to another.[4] For this specific reaction system, the total energy is the sum of the kinetic and potential energies of each substrate involved in the reaction. For the exothermic reaction F + H2, the potential energy of the products is lower than the reactants hence, the kinetic energy of the products must be higher. This is illustrated by determining a successful reaction trajectory and plotting a kinetic energy vs time graph as shown below:

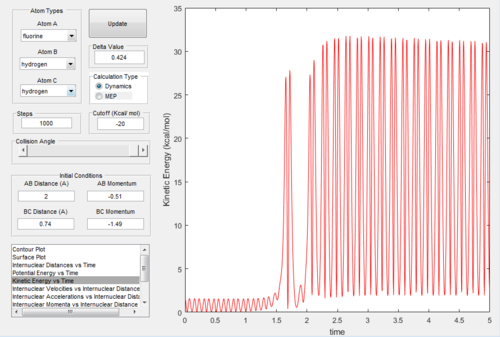
The increased kinetic energy allows the products to be detected by IR analysis. Since the H-F bond is oscillating, it will release energy in the form of vibrational energy, resulting in a peak on the spectrum. The H-H vibrational peak present on the reactant spectrum will now be absent. Another possible experimental technique is calorimetry. Since the reaction is exothermic, the amount of heat released can be measured and since, at constant pressure, the enthalpy change is equal to the net change in energy, the net free energy change of the reaction can be determined.
Q(10)
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
A:
Using trial and error, a successful reaction trajectory was found for both reactions shown below. The parameters used can be seen within the figures.
Reaction 1: F + H2 --> HF + H
Lower momentum

Higher momentum

Reaction 1, which is an exothermic reaction, exhibits an increased translational energy in response to increasing the momentum of the reactants. According to Polanyi's rules, higher translational energies are more efficient at activating an early transition state (ie. an early barrier) than vibrational energy.[5] Since early transition states resemble the reactants (as stated by Hammond's Postulate)[6], the reaction trajectory may be expected to bounce back towards the reactants. Figure 12 confirms this as an increased momentum (and therefore increased translational energy) sees the trajectory bounce back several times before eventually proceeding to the form the products. Figures 11 and 12 are an example of a set of inefficient reaction trajectories as the barrier is recrossed several times which is not ideal in the formation of the product.
The exothermic nature of the reaction also alters the position of the transition state away from the lowest 'saddle point'. This goes against the assumptions of the Transition State Theory which states that reaction trajectories should pass through this. As temperature increases, a greater proportion of excited vibrational states become occupied, leading to transition states occuring at different energies. As a result, the associated reaction trajectory at higher temperature travels through different activated complexes, making the reaction harder to model and any associated results more difficult to compare.
Reaction 2: H + HF --> F + H2
Reaction 2, which is the reverse reaction of Reaction 1, is endothermic with the energy of the products being higher than the reactants. As a result, according the Hammond's Postulate, the position of the transition state is later in the reaction trajectory and more closely resembles the products. Contrary to the preferred conditions for exothermic reactions, a larger amount of vibrational energy is needed. To achieve this, lower momentum would be adopted. Providing this is achieved, the set of reaction trajectories would be an example of an efficient reaction as the reaction trajectories would pass through the transition state once and to the products.
References
<references> [1] [2] [3] [4] [5] [6]
- ↑ 1.0 1.1 Clas.sa.ucsb.edu. (2017). Max and Min's. [online] Available at: http://clas.sa.ucsb.edu/staff/lee/Max%20and%20Min's.htm [Accessed 11 May 2017].
- ↑ 2.0 2.1 Physicsoftheuniverse.com. (2017). Quantum Tunnelling and the Uncertainty Principle - Quantum Theory and the Uncertainty Principle - The Physics of the Universe. [online] Available at: http://www.physicsoftheuniverse.com/topics_quantum_uncertainty.html [Accessed 11 May 2017].
- ↑ 3.0 3.1 3.2 Wiredchemist.com. (2017). Common Bond Energies (D. [online] Available at: http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html [Accessed 11 May 2017].
- ↑ 4.0 4.1 Mach, E. (1872). History and Root of the Principles of the Conservation of Energy. Open Court Pub. Co., Illinois.
- ↑ 5.0 5.1 Yan, S., Y.-T. Wu, and K. Liu. "Tracking The Energy Flow Along The Reaction Path". Proceedings of the National Academy of Sciences 105.35 (2008): 12667-12672.
- ↑ 6.0 6.1 Chemistry LibreTexts. (2017). Hammond’s Postulate. [online] Available at: https://chem.libretexts.org/Reference/Organic_Chemistry_Glossary/Hammond’s_Postulate [Accessed 11 May 2017].
