MRD:hyt215
Exercise 1
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The gradient of the potential energy surface at the minimum and transition structure is zero. At the minima, the components of the system are at its local minimum potential energy. This is reflected as the local minima of the potential energy surface.
At the transition state, energy only decreases in one direction, but increases in all other directions. If the potential energy can decrease in more than one direction, there would be a reaction pathway of lower energy. Thus, the saddle point of the potential energy surface would be the transition state.
(Fv611 (talk) 17:11, 16 May 2017 (BST) Good. Could have mentioned the mathematical definition (first and second order derivatives))
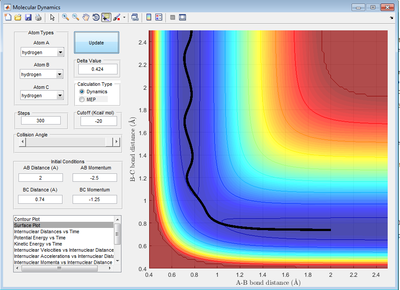
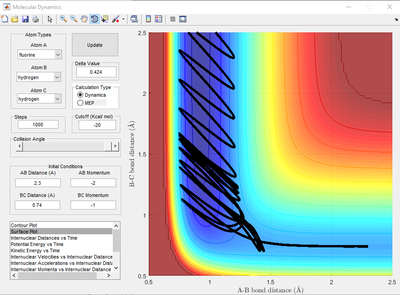
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
It is when A-B and B-C distance are both 0.908 Å. This was obtained by first finding an approximate of the intersect r1 and r2 on the internuclear distance-time graph then adjusting the AB and BC distance until the A-C and B-C bond distance is constant with time (represented by a straight line as shown in Figure X). At the transition state, the gradient of the potential energy surface is zero. Hence, it will remain at the transition state when momentum is zero.
(Fv611 (talk) 17:11, 16 May 2017 (BST) Reasoning is good, but you forgot the figure)
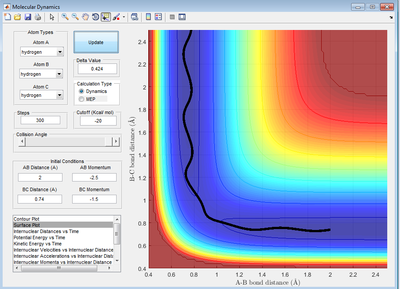
Comment on how the mep and the trajectory you just calculated differ.
The trajectory of mep is a straight line along the floor of the surface potential energy plot, following the steepest slope at each step. However, the the trajectory using Dynamic type calculation, shows an oscillating pathway which takes into account both the initial velocity and the steepest acceleration.
(Fv611 (talk) 17:11, 16 May 2017 (BST) How is the velocity treated during mep calculations?)
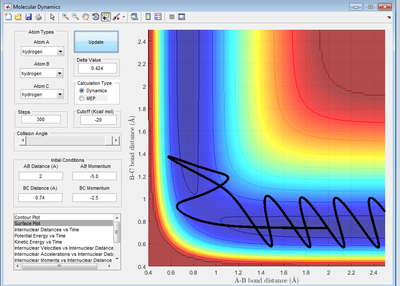
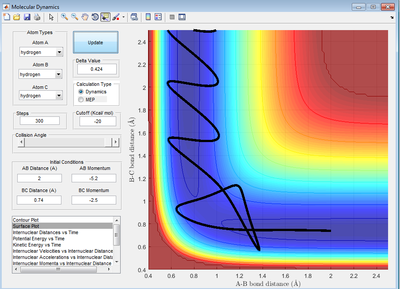
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
A successful trajectory requires A to have sufficient translational kinetic energy to overcome the activation energy. The activation energy is the saddle point of the potential energy surface, representing the potential energy of the transition state. As kinetic energy is proportional to the square of momentum, the magnitude of momentum is essential in determining that reactivity of a trajectory.
| Reaction | p1 | p2 | Reactive/ Unreactive | Trajectory | Description |
|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | Reactive |  |
As A approaches B-C, there is sufficient AB momentum such that the reactants have sufficient kinetic energy to overcome the activation energy to form A-B. This is shown as A-B bond distance oscillates about 0.75 Å as the B-C bond distance increases. The products have slightly more vibrational energy than the reactants |
| 2 | -1.5 | -2.0 | Unreactive |  |
As A approaches B-C, there is insufficient AB momentum such that the reactants do not have sufficient kinetic energy to overcome the activation energy to form A-B. This is shown as A-B bond distance decreases to about 1.1 Å then increases while the B-C bond distance remains relatively constant. |
| 3 | -1.5 | -2.5 | Reactive |  |
As A approaches B-C, there is sufficient AB momentum such that the reactants have sufficient kinetic energy to overcome the activation energy to form A-B. This is shown as A-B bond distance oscillates about 0.75 Å as the B-C bond distance increases. The products have slightly more vibrational energy than the reactants |
| 4 | -2.5 | -5.0 | Unreactive |  |
As A approaches B-C, there was sufficient AB momentum such that A-B bond is less than B-C bond for a period of time. However, the products eventually recrossed the barrier to form the reactants. Thus, the reactants are unable to overcome the activation energy to form A-B. This is shown as A-B bond distance decreases to about 0.6 Å then increases while the B-C bond distance remains relatively constant. The reactants were reformed with a higher vibrational energy than initially. |
| 5 | -2.5 | -5.2 | Reactive |  |
As A approaches B-C, there is sufficient AB momentum such that the reactants have enough kinetic energy are able to overcome the activation energy to form A-B. This is shown as A-B bond distance oscillates about 0.80 Å as the B-C bond distance increases. This trajectory shows re-crossing of products to reactants and then back to products again. This shows that the reactivity of a reaction is determined by factors other than momentum. The product formed had high vibrational energy. |
(Fv611 (talk) 17:11, 16 May 2017 (BST) Very nice discussion. Well done!)
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory assumes that when a system has sufficient energy to overcome the activation energy and reach the transition state, products will be formed
- Based on the theory, the formation of products should not lead to recrossing. Recrossing is observed in both reaction 4 and 5. In reaction 4, it was also noted that reactants was reformed despite overcoming the activation energy. This shows that having sufficient energy is not the only condition for a successful reaction. Thus, the reaction rate is overestimated by the theory.
- Based on the theory, the transition state, represented by the saddle point, has to be reached before the formation of products can happen. However, this specific point does not need to be reached. However, in collision theory, this is just an estimate and its identification should be regarded as an estimate. This is true where the trajectory does not have to pass through the saddle point identified before forming the product as shown in reaction 5.
- The theory assumes that atoms follow classical mechanics, where sufficient energy is needed for the formation of the transition state, and therefore reaction. Taking into account quantum mechanics, it is possible for atoms with insufficient energy to tunnel through the activation energy barrier. This effect is more prominent for reactions with lower energy barrier as the probability of tunnelling is higher. Quantum tunneling is not observed.
- The theory assumes that the intermediates are sufficiently long lived such that the Boltzmann distribution of energies is reached before forming products.
- This theory may not apply at high temperatures. At high temperatures, the higher virbational modes are populated and the collisions of the atoms could lead to the formation of transition states away from the lowest activation energy (saddle point).
(Fv611 (talk) 17:11, 16 May 2017 (BST) Again, a very nice discussion. Good job)
Exercise 2
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The formation of F + H2 is endothermic and the formation of H + HF is exothermic. H2 has a lower bond energy of 436 kJ mol-1 whereas HF has a higher bond energy of 570 kJ mol-1.[1] The higher the bond energy, the more stable its formation, thus being more exothermic.
(Fv611 (talk) 17:11, 16 May 2017 (BST) Good, but could have talked about the shape of the potential surface)
Locate the approximate position of the transition state.
The transition state is when rHH is 0.745 Å and rHF distance is 1.811 Å.
Report the activation energy for both reactions.
| Potential Energy/ kcal mol-1 | Ea/ kcal mol-1 | |
|---|---|---|
| F + H2 | -103.9313 | 0.1880 |
| Transition State | -103.7433 | - |
| HF + H | -133.6446 | 29.9013 |
The activation energy of F + H2 is 0.1880 kcal mol-1 endothermic and the formation of H + HF is 29.9013 kcal mol-1.
(Fv611 (talk) 17:11, 16 May 2017 (BST) The numerical value of the potential energy for E(F+H2) is wrong, and therefore the calculated activation energy is wrong)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
The reaction energy is released in the form of kinetic energy. This is reflected in the trajectory where the hydrogen fluoride has more vibrational energy than the reactant. Infrared chemiluminescence can be used to measure the infared emission of vibrationally excited molecules in the products of reaction.[2] If energy of the reacion is released in the form of thermal energy, an increase in temperature could be observed.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The efficiency of a reaction is dependent on the distribution of kinetic energy between translational and vibrational modes. Based on Polanyi's rule, vibrational energy is more efficient in promoting a late transition states than translational energy. Based on Hammond's postulate, a late transition state is endothermic whereas an early transition state is exothermic.[3] Thus, endothermic reactions such as the formation of F + H2 is more efficient when there is a higher amount of vibrational energy. On the other hand, an "early" transition state, translational excitation of the reactants is necessary in overcoming this activation energy.[3] For exothermic reactions such as the formation of H + HF, a higher proportion of energy should be in the translational mode for an efficient reaction.
To obtain an efficient reaction, an optimum balance between the translational and vibrational modes need to be obtained. While increasing the momentum of the system increases the kinetic energy, it is unable to directly control the distribution of energy.
(Fv611 (talk) 17:11, 16 May 2017 (BST) Discussion is good, but it would have been nice to provide examples for the cases you discuss)