MRD:hw7018
Excercise 1
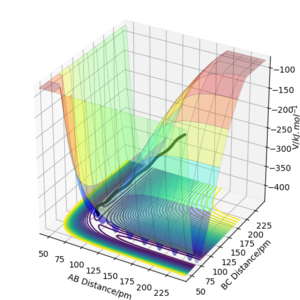
On a potential energy surface diagram, a transition state mathematically defined as ∂V(ri)/∂ri=0 (the gradient of the potential enerygy=0).
Is this true for all axis? Rs6817 (talk) 11:56, 4 June 2020 (BST)
How can the transition state be identified:
Since a small change in geometry would shift the trajectory towards either the products or the reactants at the transition state, we can start trajectories near the transition state, follow the trajectory until a point that it no longer 'roll' towards the direction before, which is the transition state.
How can it be distinguished from a local minimum of the potential energy surface: The transition state needs both ∂V(r1)/∂r1 and ∂V(r2)/∂r2=0, while the local minimum might only have ∂V(r1)/∂r1 or ∂V(r2)/∂r2=0.
Be careful with your mathematical notation here. Rs6817 (talk) 11:56, 4 June 2020 (BST)
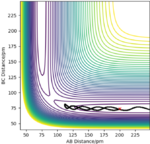
The best estimate of the transition state position (rts): rts≈ 92.4 pm
This is the intersection of rAB and rBC.
This is quite far from the transition state. This is likely due to the method you used to determine this. The forces along a TS will be 0 (no vibrational energy) and the internuclear distance vs time plot (if placed with no momenta) will be flat. Rs6817 (talk) 11:56, 4 June 2020 (BST)
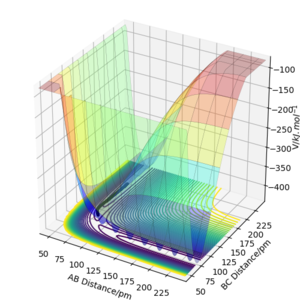
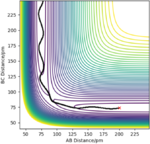
For r1=93.4 pm, r2=92.4 pm
| Dynamics | MED |
|---|---|
| r1 goes to infinity | r1 stops at ~194 pm where the new molecule is formed |
| trajectory with some vibrations because energy is still converting between kinetic energy and potential energy | smooth trajectory because no potential energy |
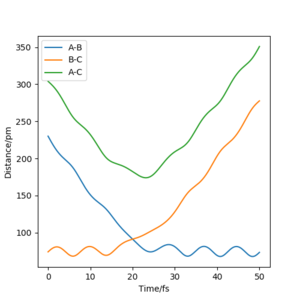
For r1=92.4 pm, r2=93.4 pm, calculation type: Dynamics, the trajectory would roll to the reactants side. rAB would decrease to ~74 pm with oscilatting and rBC would increase to infinity. pAB would increase to ~2.5 g mol-1 pm fs-1 with oscillating and pBC would increase to ~5.0 g mol-1 pm fs-1.
If set final positions and the minus final momentum (r1=74 pm, r2=351 pm, pAB=-2.5 mol-1 pm fs-1, pBC=-5.0 mol-1 pm fs-1), the trajectory would start from the reactant and roll to the product side without osciallting but stop at the transition state because it does not have enough energy to overcome the barrier.
Ok, make sure to refer to figures in a numbered format, as they appear in the text. Rs6817 (talk) 11:58, 4 June 2020 (BST)
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | reactive | smooth trajectory at first and oscillate after the transition state | 
|
| -3.1 | -4.1 | -420.077 | unreactive | trajectory with oscillation stop and reverse back at rAB~112 pm | 
|
| -3.1 | -5.1 | -413.977 | reactive | trajectory with first small oscillation and stronger oscillation after the transition state | 
|
| -5.1 | -10.1 | 357.277 | unreactive | smooth trajectory to the transition state and reverse back disorderly at rBC~130 pm | 
|
| -5.1 | -10.6 | -349.477 | reactive | smooth trajectory to the transition state and reverse back suddenly to rAB~125 pm and then proceeds to the product with irregularly large oscillation | 
|
These descriptions require more detail. Barrier recrossing is a key aspect of the last two experiments. Rs6817 (talk) 12:16, 4 June 2020 (BST)
If the value of p1 is too small (set 1) or too large (set 4 and 5), the trajectory along AB would be smooth.
If the value of p2 is too small and the total energy is too small (set 2), the trajectory would not be able to pass the transition state and revert to the reactants.
If the value of p2 is too large and the total energy is too large, there would be barrier recrossing. And if p2 is relatively small (set 4), the trajectory would revert to the reactants, while if p2 is relatively large (set 5), the trajectory would proceed to the products.
So for a reactive pathway, the system need to have a enough total energy to overcome the energy barrier and proceed to the products.
This conclusion is quite confusing. Overall what is the dependency on incoming translational and vibrational energies? Rs6817 (talk) 12:16, 4 June 2020 (BST)
When estimating Rcl in the transition state theory, all trajectories with a kinetic energy along the reaction coordinate greater than the activation energy will be reactive. But there are cases of barrier recrossing like set 5 that even the trajectory has crossed the energy barrier, the system still might revert to the reactants. Quantum mechanics allows tunnelling, so that reactants could tunnel through the energy barrier, which could be considered as the activation energy is lowered. So the experimental rate constant could be higher than the theoretical one.
Make sure you make it clear as to what youre defining as theoretical or experimental. TST tends to overpredict reaction rates. Good reference to your table Rs6817 (talk) 12:16, 4 June 2020 (BST)
Excercise 2
The approximate position of the transition state is at rHF=179.0 pm, rH2=74.5 pm
| F+H2 | H+HF |
|---|---|
| exothermic | endothermic |
| Ea≈124.5 kJ mol-1 | Ea≈116.4 kJ mol-1 |
 |
|
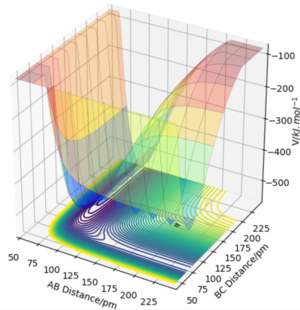
Ok, well answered and clear. Rs6817 (talk) 12:17, 4 June 2020 (BST)
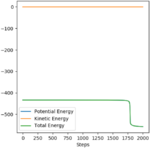
The activation energy is obtained from the energy vs. time plot with calculation type MED and steps number 2000.
The bond strength of H2 is weaker than that of HF because F is a very electronetive atom and the electrons are strongly attracted by the F atom. So the F+H2 reaction is relatively easy to undergo because less energy is required to break up the H2 molecule.
It is good you have described a method to determine the energies but it appears that your exothermic value is too high. By nudging in the product or reactant directions way from the TS, you would have been able to obtain your energies. Rs6817 (talk) 12:17, 4 June 2020 (BST)
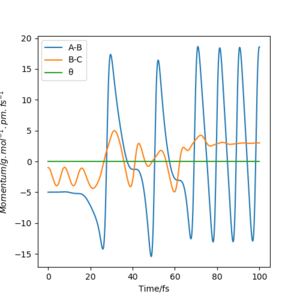
Set rHF=200 pm, rH2=74 pm, pHF=-5 g mol-1 pm fs-1, pH2=-1 g mol-1 pm fs-1. The animation shows that the H2 molecule first draws closer to the F atom with oscillation, then the central H atom oscillates between the F and the H atom. After that, the margin H atom moves away and the new HF molecule is formed with oscillaiton. From the momentum vs. time plot, the kinetic energy of H2 is converted to the central H so that it could move between the two atoms with oscillation. The kinetic energy of the central H is then converted to the potential energy of the newly-formed HF. This could be proved by measuring the F atom concentration and the H atom concentration and plot against the H2 input. There should be not much H atom formed until the HF is formed.
From pHH -6.1 to 6.1 g mol-1 pm fs-1:
at pHH= -5.1, reactive
at pHH= -4 to -2, unreactive, reaction reverse back to the reactants
at pHH= -1, unreactive, H2 and F atom do not move much
at pHH= 0 to 6.1, unreactive, H2 moves away from F atom faster with increasing pHH
Set rHF=200 pm, rH2=74 pm, pHF=-1.6 g mol-1 pm fs-1, pH2=0.2 g mol-1 pm fs-1. The trajectory is able to cross the energy barrier but reverse back to the reactants.
The Polanyi's empirical rules state that vibrational energy is more efficient in activating a late-barrier reaction than translational energy, while translational energy is more efficient for an early-barrier reaction.
Set rHF=93 pm, rH2=200 pm
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Reactive? | Illustration of the trajectory |
|---|---|---|---|
| -1 | -18 | reactive |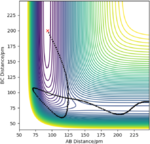 
|
| -2 | -18 | reactive |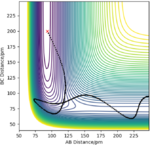 
|
| -3 | -18 | unreactive |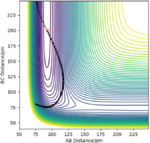 
|
| -1 | -20 | reactive | 
|
| -1 | -25 | reactive |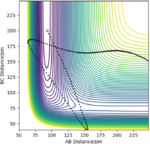 
|
| -1 | -30 | unreactive | 
|
The H + HF reaction is a late-barrier reaction. From the table, a small increase in the value of p1 would shift reactive to unreactive, while a large increase is needed for the value of p2 to achieve the same effect, which is in consistent with the Polanyi's empirical rules.
Good answer for this last bit and well explored with your table. Am not sure if the penultimate example can be considered as reactive? Rs6817 (talk) 12:19, 4 June 2020 (BST)