MRD:hsh16

Exercise 1: H + H₂ system

Question 1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

Each component of the gradient of the potential curve will have a value of 0 ie: ∂V(r_i)/∂r_i = 0

Minima and transition states can be distinguished by taking the second derivative of the potential energy curve ie: ∂²V(r_i)/∂r_i². Minima, as the name suggests, will have a second derivative with a value > 0 at that coordinate for all components of the gradient. Transition states, which are energy saddle points, will have a second derivative with a value < 0 for one component and > 0 for the other at that particular coordinate.

Question 2: Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Question 2: The internuclear distance vs time plot for the transition state of the H-H-H system.

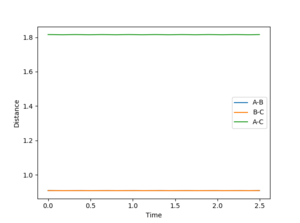
r_ts = 0.908 Angstroms

The Internuclear Distance vs Time plot is shown on the right, with p_AB = 0 and p_BC = 0.

The plot shows a constant separation between all the atoms present in the system, implying that the atoms remain stationary and that no bonds are formed (the H-H bond length is shorter than the transition state separation at 0.74 Angstroms) in the system so long as the system is undisturbed.

Question 3: Comment on how the mep and the trajectory you just calculated differ.

Question 3: The MEP plot.

Question 3: The dynamic plot.

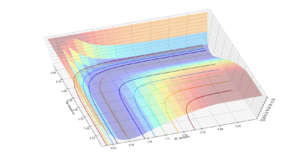
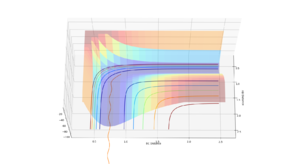
The MEP plot differs from the dynamic one as it does not display the oscillation and resulting perturbations in potential and kinetic energy associated with the vibration and translational movement of the hydrogen molecule. This occurs because the computation takes the minimum energy path at each step which involves a constant atomic separation/bond length. Any deviation from the equilibrium separation from the molecule's vibration leads to an increase in kinetic energy due to the parabolic nature of the oscillator energy curve.

Question 4: Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

p1	p2	Total Energy (kJ mol-1)	Does it react?
-1.25	-2.5	-99.018	Yes.
-1.5	-2.0	-100.456	No.
-1.5	-2.5	-98.956	Yes.
-2.5	-5.0	-84.956	No.
-2.5	-5.2	-83.416	Yes.

Jas213 (talk) 17:07, 13 May 2018 (BST) Correct results, but very little explanations. No headers, no word about the methodology, just basic question and answer. You're not mentioning what reaction you are discussing here. A title or the equation of the reaction would have been useful, stating the starting conditions and what calculation type you used. Then a concluding comment below all the trajectories of what you learned from this table, would have been expected.

Question 4.1: The system reacts and moves into the product channel, forming a new H-H bond.

Question 4.2: The system does not react, rolling back into the entrance channel and reforming the initial H-H bond.

Question 4.3: The system reacts and moves into the product channel, forming a new H-H bond.

Question 4.4: The products form, before the excess kinetic energy causes it to recross the transition state barrier and reform the reactants.

Question 4.5: The products form, recross the barrier to reform the products before reacting again to finally form the product.

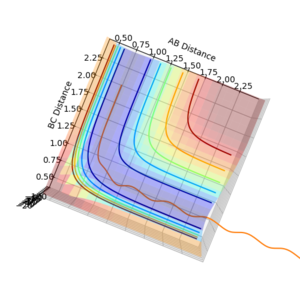
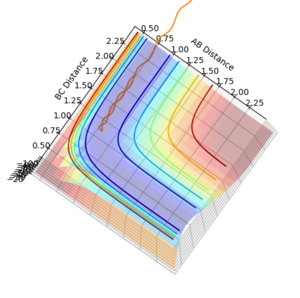
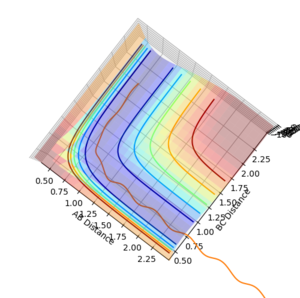
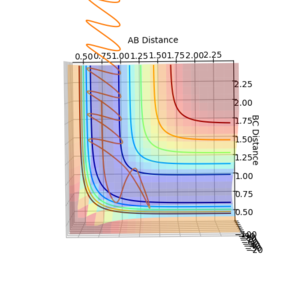
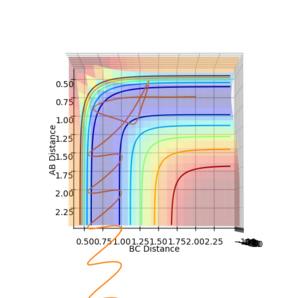
Question 5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition state theory first assumes the Born-Oppenheimer approximation (that nuclear and electronic motions are separate) and that reactant molecules follow the Maxwell-Boltzmann distribution. In addition to those two fundamental assumptions, transition state theory also requires the follwoing:

1) Systems of molecules which have overcome the transition state barrier to become products cannot do the reverse to reform reactants.

2) Motion along the reaction coordinate in the transition state can be treated classically as a translation. This motion is also considered as being separate from other modes of motion.

3) Transition states becoming products are distributed according to the Maxwell-Boltzmann laws. This occurs even if an equilibrium between reactant and products does not.

With the results of the previous sections in mind, the transition state theory predictions of rate constants will be higher than the empirical values as it neglects instances of products re-crossing the transition state barrier to reform the reactants (as is observed in the penultimate case of the previous quesion, where barrier re-crossing occurs, defying the first additional assumption described above). This recrossing can even occur multiple times, as particles might need to adopt a specific orientation when colliding in order to react in reality.

EXERCISE 2: F - H - H system

Question 1: Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The F + H₂ reaction is exothermic. This can be justified by the bond energies associated with the reaction and by the fact that bond breaking is endothermic while bond formation is exothermic. There is less energy required to break the H-H bond (ca. 432 kJ mol^-1) than is released when the H-F bond is formed (ca. 565 kJ mol^-1).

Meanwhile, the HF + H reaction is endothermic as there is more energy associated with the breaking of the H-F bond than is released by the formation of the H-H bond.

Question 2: Locate the approximate position of the transition state.

F-H distance is ca. 1.810 Å. H-H distance is ca. 0.746 Å.

Jas213 (talk) Where is a plot of the reactive pathway? Where is a plot proving that this is the actual transition state? Did you do an MEP on it? What was your method for finding the transition state?

Question 3: Report the activation energy for both reactions.

The activation energy was taken as the difference in potential energy between the starting position (neighbouring the transition state) and the final position of the system as follows.

Activation energy of F + H₂ = 0.268 kJ mol^-1 (Taking r_F-H = 1.82 Å and r_H-H = 0.75 Å)

Activation energy of HF + H = 30.132 kJ mol^-1 (Taking r_F-H = 1.80 Å and r_H-H = 0.74 Å)

Question 4: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The reaction energy is transferred into kinetic energy in the form of excited translational and vibrational modes of the products. The excited modes are determined by the nature of the potential energy surface of the reaction. For a repulsive energy surface that has a late release in its exoergicity, the energy is tranferred predominantly into its translational modes, with the final system having less excitement in its vibrational modes. Conversely, a reaction with an early release of exoergicity will lead to products that are vibrationally excited with less excitement in its translational modes.

F + H₂ has an early release of exoergity, which leads to the final H-F molecule being highly vibrationally excited, which can be observed in the large pertubations in potential energy observed in 4.2.

Question 4: The internuclear momenta vs time plot. The large A-B (H-F) momenta indicates large vibrational excitation in the H-F molecule when it finally forms.

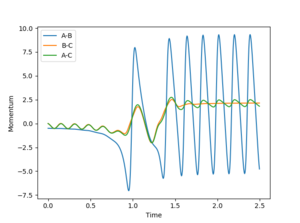
Experimentally, confirming either could be done with measurements of pressure and detection of infra-red emissions on the infra-red spectrum. Assuming that there all the species present in the system being investigated are gaseous, and that the overall number of gaseous particles in the system remain constant over the experiment (as is observed with both reactions in this exercise) an increase in translational energy of the particles present would manifest itself as an increase in the pressure of the system as the collisions of the gas with the walls of the container become more forceful.

Meanwhile, vibrationally excited molecules would emit radiation in the infra-red region of the electromagnetic spectrum via internal conversion upon relaxation to their ground state. The detector in this case should be tuned specifically to detect quantised emissions of infra-red radiation, instead of plainly measuring the temperature of the system (as both excited vibrational and translational modes will lead to an increase in temperature).

Alternatively, one could examine the structure of any emissions of electromagnetic radiation obtained for the Doppler effect, using that to make a conclusion. Observed Doppler broadening implies a greater excitation of translational modes in the sample. Narrowed spectral emissions imply the opposite, with less excitation of its translational modes.

Question 5: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's empirical rules state that vibrational energy is more effective in promoting a reaction with a late transition state. This occurs as the molecule needs to have the correct phase of vibration in order to overcome the barrier, which in turn implies a large vibrational energy requirement from the reactants. An excess of translational energy will lead to the molecules colliding with the repulsive inner wall of the potential energy surface to roll back into the reactant channel. Meanwhile, while translational energy is better at promoting a reaction with an early transition state. Molecules with excessive vibrational energy here will not have enough energy to overcome the barrier, instead vibrating side-to-side in the entrance channel.

With this in mind, the reactions considered above should be classified according to the position of their transition states in the context of Hammond's postulate. The postulate states that the transition state of a reaction most resembles the species nearest to it in energy.

From its extremely low activation energy, it can be inferred that the F + H₂ reaction has a very early transition state, which, by Hammond's postulate, heavily resembles the reactants. For this reaction to be efficient, the system would have to have a greater distribution of its energy in translational modes.

Conversely, the HF + H reaction has a very late transition state that greatly resembles the products. Polanyi's rules therefore require that the system have a large amount of vibrational energy for this reaction to occur.

Jas213 (talk) 17:32, 13 May 2018 (BST) Good use of references. Nice that you mentioned Polanyi's rules. However, it's a shame that you didn't discuss the Polanyi concepts you are citing with example reaction trajectories, applying different momenta as done for the H+H2 reaction. Show a bit more of your own working next time.