MRD:gmg216
Dynamics from the transition state region
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
r1 = RAB, r2=RBC
The first exercise deals with a 3 hydrogen system, and the reaction H + H2 > H2 + H
The gradient of a potential energy surface is defined by ∂V(r)/∂r. The transition state is the maximum of the minimum energy path (on a saddle point) so ∂V(r)/∂r=0. The products and reactants are at minimum points where the gradient with respect to r1 and r2 is 0. For a maximum or minimum point the second derivative is also equal to 0.
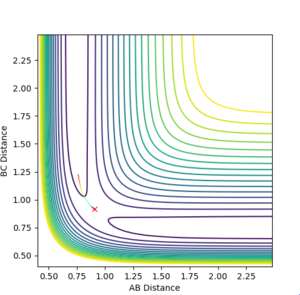
Mm10114 (talk) 23:18, 28 May 2018 (BST) Are you sure about the last part? What about the second partial derivatives for the saddle point in the direction of the reaction and orthogonal to it? Revisit the "Dynamics from the transition state region" figure from the workshop's wiki. In the end you didn't show how, using calculus - relating to the curvature of the PES, minimum and TS can be distinguished.
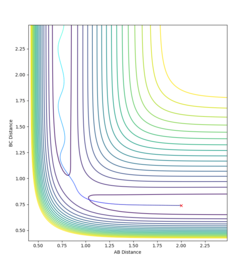
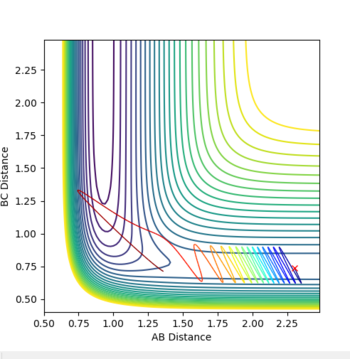
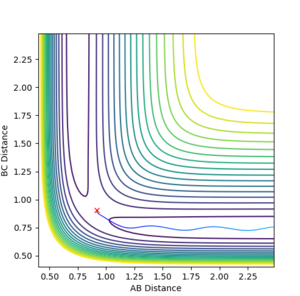
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
Each particle is given 0 momentum and both the initial distances RAB and RBC are set equal. When both particles have 0 initial momentum the initial distances can be varied to find the transition state. If internuclear distance as a function of time is plotted, when both RAB and RAC are set to 0.908, it can seen that the internuclear distances stop oscillating and remain constant. The particles are sat at the bottom of a potential energy well, and cannot oscillate at the bottom of the well as they have no momentum.
Mm10114 (talk) 23:18, 28 May 2018 (BST) This is good. However, you wrote "The particles are sat at the bottom of a potential energy well", where exactly? You have to be more specific (some visual aid in form of a figure?), because here it does not specify you mean the potential well orthogonal to the direction of the reaction pathway (at the saddle point).
MEP and dynamic analysis
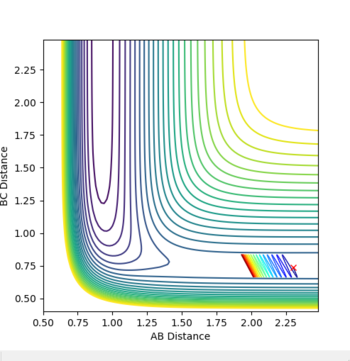
An dynamic and MEP analysis were run when RAC was the transition state distance, while RBC was the transition state distance + 0.01.
 |
 |
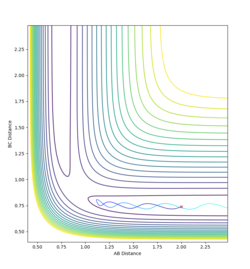
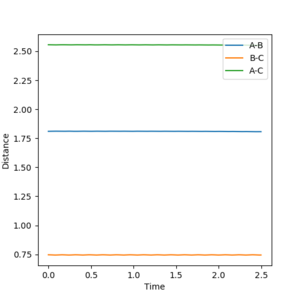
For internuclear distance vs time for the dynamic RBC tended to infinity, with a value of 10 at large time. RAB levelled off at 0.4 with oscillation. For the MEP AB leveled off at 0.4, with BC tending to infinity with the value 2.2 at large time. There was no oscillation for the MEP values.
Mm10114 (talk) 23:18, 28 May 2018 (BST) Would be good to have the unit of distance reported by now.
For time vs momemtum, the MEP momentum was constant at 0. The AB momentum leveled off at 1.2, with heavy oscillation, while the BC momentum leveled off at 2.5 with no oscillation. In the trajectory the energy oscillates, while there is no oscillation in the MEP. This is because the velocity is reset to 0 at each step, and therefore the MEP has no initial momentum. Oscillation requires going energetically uphill - which the MEP cannot do as it does not have any initial energy.
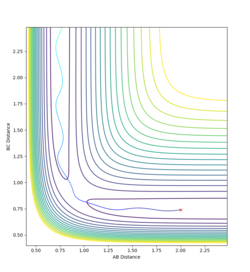
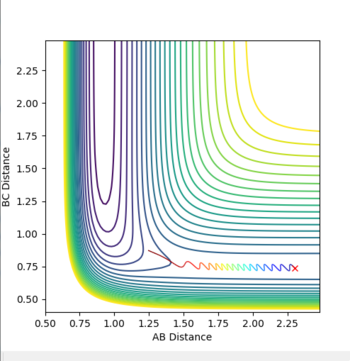
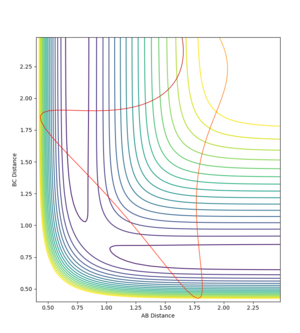
A trajectory was run switching the values of RAB and RBC. All that changed was that the particles approached from the opposite channel. When a dynamic trajectory was created with the conditions at the limit the particles had so much energy they travelled right up the sides of the potential energy well, avoiding the reason state. When the MEP was created for conditions at the limit the trajectory was unreactive. The particles had no initial momenta, so could only energetically roll downhill on the potential energy surface until they ran out of energy.
 |
 |
 |
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
| P(AB) | P(BC) | Trajectory | Total energy | Reactive or unreactive |
|---|---|---|---|---|
| -2.5 | -1.25 | 
|
-99.119 | Reactive. The molecule has enough energy to reach the transition state and travel over the saddle point and form the products. |
| -2.0 | -1.5 | 
|
-99.119 | Unreactive. The molecule does not have enough energy to pass over the saddle point and the transition state is not reached. |
| -2.5 | -1.5 | 
|
-99.119 | Reactive. The molecule has enough energy to reach the transition state and travel over the saddle point and form the products. The oscillation is greater than the first also reactive trajectory because the momenta are more negative. |
| -5.0 | -2.5 | 
|
-99.199 | Unreactive. The molecule has enough energy to reach the transition state, but has so much energy that it does not travel over the saddle point, but instead moves back into the reactant area of the potential energy surface. |
| -5.2 | -2.5 |  |
-99.199 | Reactive. The molecule has enough energy to reach the transition state and travel over the saddle point and form the products.The momenta for both AC and BC are large so the molecules oscillate on up and down the sides of the potential energy well. |
Mm10114 (talk) 23:18, 28 May 2018 (BST) Total energies for all systems are the same, should they be? Otherwise, good observations.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
1. Quantum tunnelling effects through the potential energy surface are assumed to be negligible, so reactants must pass over the saddle point to the product point. 2. The reactants are assumed to be in thermal equilibrium, with energies distributed according to the Boltzman distribution. 3. That there is only one saddle point on the potential energy surface and hence one transition state between reactants and products.
The state distribution of reactants will cary heavily according the to temperature, due to the Boltzman distribution. Therefore at low temperatures higher energy states will be inaccessible and the transition state may not be able to be reached by the reactants. At extremely high temperatures, many more states will be accessible and therefore molecules may be able to access higher energy of multiple transition states. Therefore, it can be assumes transition state theory is accurate at mid-range temperatures and for situations in which quantum tunnelling is negligible.
Mm10114 (talk) 23:18, 28 May 2018 (BST) A good discussion. However, where did you take these TST assumptions from? Missing a reference.
Exercise 2
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The H-F bond is significantly stronger than the H-H bond, which is significantly stronger than the F-F bond. The H-H bond has an enthalpy of 436KJ/mol-1 while the H-F bond has an enthalpy of 565KJ/mol-1 and the F-F bond has an enthalpy of 155KJ/mol-1. Therefore:
H2 + F → HF + H is exothermic
HF + H → H2 + F is endothermic
Report the activation energy for both reactions.
Hammond's postulate states that structure of a reactant, product of intermediate can be predicted by comparing its energy to the species neighboring it along the reaction coordinate. In an exothermic reaction the transition state is closer in energy to the reactants than the products. Therefore, the transition state structure will resemble the reactants rather than the products.In both cases the transition state radius will be close to the radius of H2 at 0.74. The activation energy was taken from the energy vs time graph. At the start, the energy decreased vertically between two values and became more negative before remaining constant. The difference between these two energy levels is the activation energy.
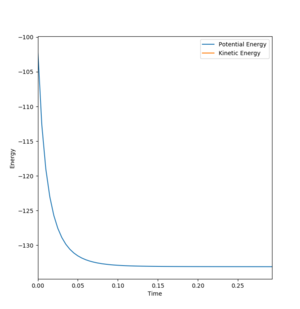
Mm10114 (talk) 23:20, 28 May 2018 (BST) That's good. But, you only show the plot for HF + H → H2 + F reaction, why not the other? As you report activation energies for both reactions.
| Reaction | Rab at transition state | Rac at transition state | Activation energy (KJ/mol-1) |
|---|---|---|---|
| H2 + F → HF + H | 1.81 | 0.746 | 0.727 |
| HF + H → H2 + F | 0.746 | 1.81 | 31.6 |
 |
 |
 |
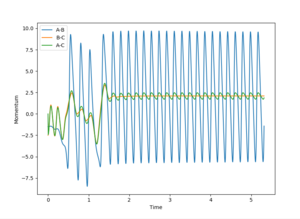In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
H2 colliding with F is an exothermic reaction, because the enthalpy of the new bond formed is greater than the enthalpy of the bond broken. However, the energy must be conserved. It can be seen from the momentum time graph that the vibrational energy is substantially greater in the product. Therefore the excess energy from the collision is converted into vibrational energy. This is dissipated by collisions of the HF molecules and is converted into kinetic energy. As temperature is the average kinetic energy of the molecule this can be quantatively measured by either temperature change or caliometry.
| PFH | PHH | Trajactory | Reactive or unreactive |
|---|---|---|---|
| -0.5 | -3 | 
|
The momenta of the H-H bond is high, so the bond has a high vibrational energy, while the HF momentum is low meaning that the F atom approaches with a low velocity and has low translational energy. Exothermic reactions usually depend on high translational energy to be successful, so there is not enough translational energy to cross over the barrier. The molecules therefore 'bounce off' the energy barrier and return to the reactant channel. |
| -0.5 | -2 | 
|
The vibrational energy of the H-H bond is decreased and the translational energy remains low. Therefore the reactants do not have enough energy to leave the reactant channel. |
| -0.5 | -1 | 
|
The vibrational energy of the H-H bond is decreased and the translational energy remains low. Therefore the reactants do not have enough energy to leave the reactant channel. |
| -0.5 | 3 | 
|
The vibrational energy is higher so the H-H bond has high vibrational energy, but the translational energy of the colliding H atom is still not high enough to cross over the energy barrier. |
| -0.8 | -0.1 | 
|
The momentum of the colliding H atom is now greater so the reactants move further along the reactant channel. However due to the lowered vibrational energy of the H-H bond the reactants cannot travel over the energy barrier and remain in the reactant channel. |
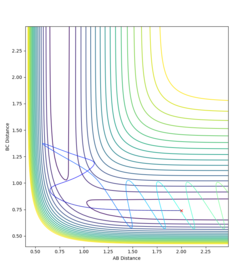
As the momentum of H-H gets larger(either more positive or more negative) the particle oscillates higher up the sides of the potential energy surface.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The initial condition were set for RBC=0.91 (H-F bond length) RAC=2.3 and both momenta set to 0. A low vibrational motion was produced on the H-F bond (PHF=0.1) while a high momentum was introduced on the H atom(pHH=5). This gave the H atom high translational energy. This did not give a reactive trajectory as the transition state was not reached. A reactive trajectory was eventually found by increasing the vibrational energy on the HF bond to 6.89 and decreasing the translational energy of the hydrogen atom to -1.
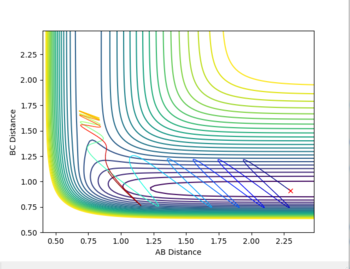
Polanyi's rules give the most effective form of energy for crossing on energy barrier. This reaction is endothermic. Therefore there is an late energy barrier - as the transition state structure is more similar to the products than the reactants. Kinetic, or translational energy, is not effective at crossing this barrier. The potential energy of the particles rises as they appraoch the barrier, taking them up the sides of the potential energy well. Therefore they are reflected back into the reactant region despite there being enough energy for the reaction to proceed. The particles effectively collide with the energy barrier and bounce back off it.
Vibrational energy causes the molecule trajectory to weave side to side (or oscillate) as it apporached the saddle point. This motion can cause the molecules to reach and travel over the saddle point. Therefore, when the vibrational energy of the HF bond is increased and the translational energy of the H atom is decreased the reaction is successful as there is enough vibrational energy to overcome the barrier. However, the product is not vibrationally excited. This can be seen in the momenta vs time graph:
If the reaction was exothermic high translational energy is required to move past the early energy barrier, and results in a vibrationally excited product.
Mm10114 (talk) 23:23, 28 May 2018 (BST) Your discussion is good and you state Polanyi's rules. However, where is the citation of the source for Polanyi's rules. You need to clearly state where you've taken these from.