MRD:gm1110

Grace's MRD Page

EXERCISE 1: H + H₂ system

Q1: What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

Energy minima correspond to physically stable chemical species, whereas transition structures are represented on a potential energy surface as saddle points. These are both stationary points of the surface so have a gradient of zero. However, as saddle points correspond to a maximum energy along the lowest energy pathway, this means they are distinguishable from minima as the saddle points are also a local maxima for a function along the orthogonal axis.

(Fv611 (talk) 14:30, 9 June 2017 (BST) Correct, but should have discussed how to determine if a point is a maximum or a minimum. Hint: the second derivative of potential energy with respect to the displacement along the reaction coordinate corresponds to the curvature of the PES.)

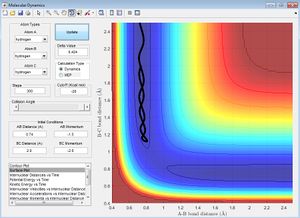
Q2: Report your best estimate of the transition state position (r_ts) and explain your reasoning, illustrating it with a "Internuclear Distances vs Time" screenshot for a relevant trajectory.

My best estimate for r_ts is r₁=r₂=0.908A.

When the reactants are still moving towards each other, a graph of internuclear distances against time shows the molecules approaching each other, passing through the transition state and the other atom being spat out. The point where the lines representing the A-B distance and B-C distance cross represents the transition state, and as the atoms are all homonuclear, the distances r₁=r₂ so the lines lie on top of one another as seen in the diagram above.

As the transition state is the maximum point along the minimum energy pathway, this means that when the system is in the transition state, it stays there until a small perturbation is applied to the system, at which point it will collapse into either the reactant or product pathway channels. So it was possible to check the estimated transition state position of r₁=r₂=0.908 A by changing p₂=±0.00001, and seeing the reaction pathway run down the reactant pathway and products pathway.

(Fv611 (talk) 14:30, 9 June 2017 (BST) Good, could have also commeneted that the system barely oscillates at the TS)

Q3: Comment on how the mep and the trajectory you just calculated differ.

Using initial parameters of r₁=0.908 A and r₂=0.918 A with p₁=p₂=0, trajectories using both the MEP and the dynamics calculations were predicted.

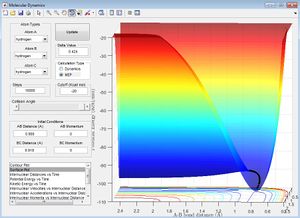
As can be seen in the figure, the MEP calculation predicts a straight line that follows the minimum energy along the bottom of the "valley" in the surface plot.

As can be seen in the figure, the dynamics trajectory still follows the minimum energy path along the bottom of the "valley" but also oscillates from side to side. The oscillations correspond to vibrations between the atoms, and therefore contains more information that the trajectory calculated using the MEP.

(Fv611 (talk) 14:30, 9 June 2017 (BST) You describe the effects, but not the cause. Why is the mep trajectory straight instead of oscillating like the dynamic one?) Using the same initial conditions, we then viewed the plots of internuclear distance against time and internuclear momenta against time.

In the internuclear distance vs time view, the dynamic plot shows the AB,BC and AC plots as straight lines that lie one on top of each other. The mep view shows the AB distance decreasing a little, then plateauing off into a straight line, whereas the BC distance looks like the top of a ln graph with a slow exponential start.

For large values of t, it was found that the final values of the positions and the average momenta were r₁=0.756, r₂=186.4, p₁=1.240 and p₂=2.481 respectively.

Switching the parameters around so that the initial positions correspond to the final positions of the calculated trajectory and the same final momenta values but with their signs reversed, it was observed on a surface plot that the trajectories were the same, but going in the reverse direction, as expected.

Q4: Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

For initial positions of r₁=0.74 and r₂=2.0, the following table:

caption
Trajectory number	p₁	p₂	Reactivity
1	-1.25	-2.5	Reactive
2	-1.5	-2.0	Unreactive
3	-1.5	-2.5	Reactive
4	-2.5	-5.0	Unreactive
5	-2.5	-5.2	Reactive

For trajectory 1, we see that there is a crossover of the red and blue lines, indicating that atom C has approaches AB as the internuclear distance gets smaller, and then the BC bond distance remains constant as the AB bond distance increases, indicating that A is now leaving the newly formed molecule BC. Hence it is reactive.

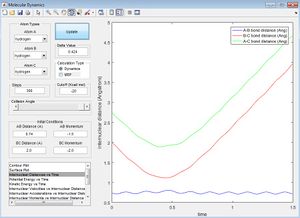
For trajectory 2, we see that the red and blue lines do not intersect, indicating that the incoming atom C bounces off of AB without reacting.

(Fv611 (talk) 14:30, 9 June 2017 (BST) Actually if C did bounce off AB they would intersect and then separate again. C doesn't have enough energy to react in this case.)

For trajectory 3, we see that the react.

For trajectory 4, we see that they do not react as C moves away from AB in the end.

For trajectory 5, we see that they do react.

Q5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.[1] This basically states that for a chemical reaction A+B ↔ [AB]^‡ ↔ C, where A and B are reactants and C the product, that the formation of [AB]^‡ from the reactants and the reverse formation of [AB]^‡ from the products are independent of each other.

Transition state theory assumes that atomic nuclei behave according to classical mechanics in a collision, meaning that a transition state will not be formed unless the molecules collide with enough energy to form a transition state. However in reality, quantum mechanics states that it is still possible for a pair of molecules to react even if they do not have sufficient energy via quantum tunnelling. Whilst negligible for reactions with high energy barriers, the added effect of quantum tunnelling becomes more significant as the probability of occurrence increases with decreasing barrier height. The added quantum tunnelling effect would therefore lead to a faster reaction rate than predicted from transition state theory alone.

The theory also assumes that any reaction system will pass through the lowest energy saddle point of a potential energy surface contour. Whilst this assumption holds at lower temperatures, this is not necessarily the case in higher energy gas-phase reactions such as the co-linear approach of H to H₂. In high energy reactions, it is found that the motion of the atoms becomes much more complex as they occupy higher energy vibrational levels, and can lead to the transition state moving off the saddle point and into the reactant and product channels.

(Fv611 (talk) 14:30, 9 June 2017 (BST) Good, but you do not discuss how does TST deal with the system crossing the TS multiple times.)

EXERCISE 2: F - H - H system

(Fv611 (talk) 14:30, 9 June 2017 (BST) The whole exercise is missing.)

Q6: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The average H₂ bond length is 0.74A, and the average HF bond length is 0.91A.

Firstly considering the reaction F + H₂, set the initial distance of F-H as r₁=1.2A and the initial distance of H-H as r₂=0.74A with momentum p₁=-0.9 and p₂=0 respectively. A plot of potential energy against time shows that the potential energy falls from the initial -106.4kcal/mol to an average potential energy of (-133.9-114.8)/2, indicating that the reaction is exothermic.

Now considering the reaction H + HF, set the initial distance of H-H as r₁=1.2A and the initial distance of H-F as r₂=0.91A with momentum p₁=-0.9 and p₂=0 respectively.

Q7: Locate the approximate position of the transition state.

Try to set the H-F distance maybe at about 1.7 (transition state somewhere in reactant channel) and fiddle with momentum 0 until you find it. The H-H distance will be roughly somewhere half-way along where the oscillations are.

References

[1] http://goldbook.iupac.org/html/T/T06470.html for stuff on transition state theory

[2] H. Eyring "The Activated Complex in Chemical Reactions", J. Chem. Phys. 3 (1935) (http://aip.scitation.org/doi/pdf/10.1063/1.1749604)

[3] R. Masel "Principles of Adsorption and Reactions on Solid Surfaces", New York, Wiley (1996)

[4] J.R. Pineda, S.D. Schwartz "Protein Dynamics and Catalysis: The Problems of Transition State Theory and the Subtlety of Dynamic Control" Phil. Trans. R. Soc. B. 361 (1472) (http://rstb.royalsocietypublishing.org/content/361/1472/1433)