MRD:fabianthomaslabphyscomp
EXERCISE 1: H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface?
The total gradient of a potential energy surface at a minimum and a transition structure is equal to zero. Minima and transition states can be distinguished by looking a the second derivative of the potential energy surface. If the second derivative is also equal to zero then then the point is a saddle point and so relates to a transition state, whereas if the result is positive, then the point is a minima
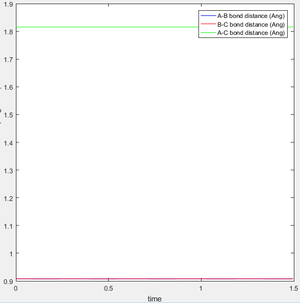
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
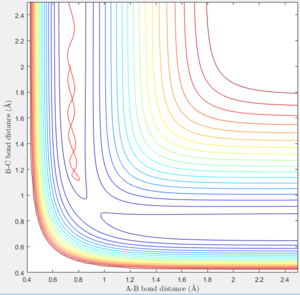
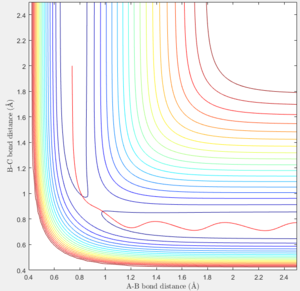
The location of the transition state is rts = 0.9077 ± 0.0001Å. The transition state is a saddle point in the potential energy surface with the highest potential energy along the reaction coordinate. If the molecules is placed at the transition state with no kinetic energy, the molecule will not oscillate or move and as a result the internuclear bond distances will not change. As it can be seen in figure 1, the internuclear bond distance does not change, and therefore this conformation can be seen to be the transition state.
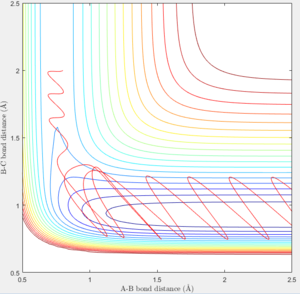
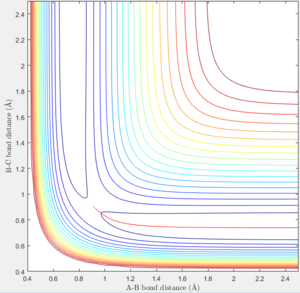
Comment on how the mep and the trajectory you just calculated differ.
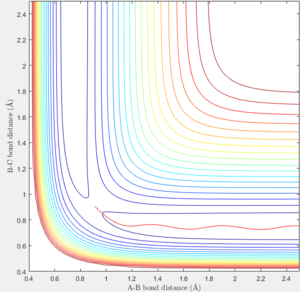
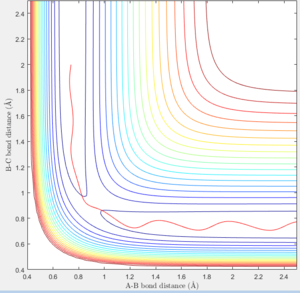
The mep plot corresponds to the path of minimum potential energy away from the molecule B-C for atom A with increasing A-B distance, while in the dynamic plot atom A oscillates about the minimum potential energy path with increasing A-B distance. This can be seen in figures 2 & 3. A change is seen if the internuclear distance of B-C is changed instead of A-B with the graph being reflected across the y=x axis. If doing the calculation in reverse, by using the final positions and reversing the momenta of the AB and BC with variables r1 = 4.666, r2 = 0.7451 p1 = -2.485 p2 = -1.512, the plot reaches the original variables used in figures 2 & 3, before returning along the same path it traveled.
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Reactive? |
|---|---|---|
| -1.25 | -2.5 | Yes |
| -1.5 | -2.0 | No |
| -1.5 | -2.5 | Yes |
| -2.5 | -5.0 | No |
| -2.5 | -5.2 | Yes |
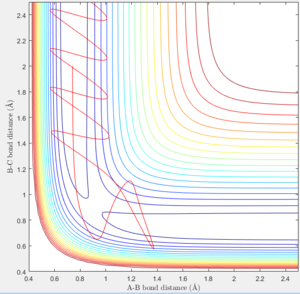
- In figure 5, atom C approaches molecule A-B with constant velocity and displaces atom A and forms molecule B-C.
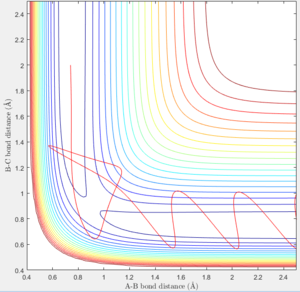
- In Figure 6 atom C approaches the molecule A-B with constant velocity, but is rebounded.
- In Figure 7 atom C approaches molecule A-B with constant velocity and displaces atom A and forms molecule B-C.
- In Figure 8 atom C approaches the molecule A-B with sinusoidal motion ,but is rebounded.
- In Figure 9 atom C approaches molecule A-B with constant velocity and displaces atom A and forms molecule B-C.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory assumes that atoms and molecules move under classical mechanics, without quantum effects, and that there is only one possible transition state which is the lowest energy conformer and also can be stablised as shown in figure 1. Transition State Theory will give reaction rates that are higher than experimental rates.
EXERCISE 2: F - H - H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 reaction is exothermic, and the H + HF reaction is endothermic. H-F has a higher bond energy than H-H and therefore does relate to the equations and one would expect to see that the F + H2 to give H + HF would release energy due to the increased bond strength, which is seen in the program.
Locate the approximate position of the transition state.
The approximate location of the transition state, using Atoms A, B and C as H, H and F respectively is AB = 0.8Å and BC = 1.49Å
Report the activation energy for both reactions.
The activation energy for HF + H is approximately 8500 J/Mol, and H2 + F is approximately 10500 J/Mol
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
The mechanism for the release of energy from a reaction as energy is conserved, is through heat (or light). For an exothermic reaction which therefore releases reaction energy, the energy of the particles released is greater than the reactant particles at the start of the reaction which one can see in figure 10 where the oscillations of the H atom after being extruded from the molecule are much larger, and the path crosses a much higher potential energy surface, thus showing that energy is released from the reaction through kinetic energy
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Vibrational energy modes in reactions that have an early transition state do not effect the reaction much as the transition state resembles the reactants more than the products. This means the bond that is breaking will be more formed and so vibrations will not effect the bond breaking process much as that occurs after the transition state has been crossed. In contrast, for a reaction with a late transition state (endothermic) the transition state will have the bond that is breaking closer to breaking than not, and so an increase in vibrational energy of the bond could help to break the bond due to larger oscillations in the bond. This is the opposite for transitional energy as for a late transition state, the bond is almost already broken and so the reactants do not need to get any closer to each other. An increase in energy too high would lead to a reactant bouncing off the other due to the speed of the approaching molecules. This can effect the efficiency of the reactions as if a molecule has lots of vibrational states and an early transition state, an increase in energy would add much more vibrational energy than translational energy and so would not effect the reaction speed as much as if it had less vibrational states, due to the larger increase in kinetic energy the molecule would gain. Therefore the distribution of energy between translational and vibrational states effects the efficiency of reactions.