MRD:ew515
Dynamics of the H - H - H System
Transition State Position

At a minimum or a transition state (maximum), the potential energy surface for a reaction will have a gradient of zero. Using Molecular Dynamics, these states will be stable if the atoms are given no relative momenta. Furthermore, these cases can be distinguished from one another by perturbing the internuclear distances—in which case a minima would be stable (retain original bond distances over time), while a transition state would fall to some other potential energy minima (change bond distances).

(Fv611 (talk) 14:41, 9 June 2017 (BST) Ok, but the is a saddle point, not a maximum. It is only a maximum in the direction of the reaction coordinate. There is a mathematical way of distinguishing minima, maxima and saddle points.)
In the case of the symmetrical H+H2 reaction, the transition state would also have equivalent internuclear bond distances, such that r1 = r2. To identify this transition state bond distance, rts, the internuclear bond distance vs. time plot was checked for the time at which the r1/r2 bond distances are equal (x = 0.38, r1/r2 = 0.91 angstroms). It is noted that this time value did not agree with those of the global potential energy maximum (x = 0.455) and the global kinetic energy minimum (x = 0.455).
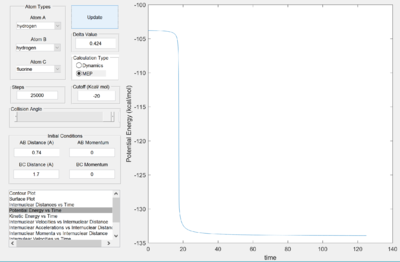
However, relying on the symmetry requirement of the H--H--H transition state, the internuclear bond distance of 0.91 angstroms was carried on to establish the transition state bond length. Various bond distances were then simulated within .01 angstroms of 0.91 while seeking to minimize the symmetrical transition state vibrations visualized in the kinetic energy plot (as at the transition state, the kinetic energy and such vibrations are at a minima). An rts value of 0.907 angstroms, with no relative momenta, yielded internuclear distance (Fig. 1) and kinetic energy (Fig. 2) plots seen to the right. As expected, internuclear distances were maintained over the duration (300 steps), while subtle symmetrical vibrations are also seen.
(Fv611 (talk) 14:41, 9 June 2017 (BST) Ok, but why didn't you mention what the internuclear distances were at x=0.455?)
Minimal Energy Path Vs. Dynamics Path
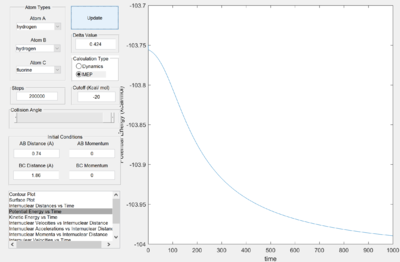
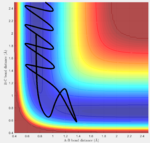
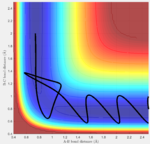
Reaction trajectories from one side of the transition state (r1 = rts + 0.1, r2 = rts) were simulated using the minimum energy pathway (Fig. 3), or mep, and the "Dynamics" pathway (Fig. 4). While, the minimum energy pathway is seen to proceed along the minimal energy valley towards the products, with no molecular vibrations, the dynamic trajectory illustrates the continuing vibrations of the central hydrogen atom with the bonding hydrogen atom (seen as oscillations in rA-B) as the leaving atom disassociates.

(Fv611 (talk) 14:41, 9 June 2017 (BST) You are describing the effects, not the cause. Why is the mep trajectory a straight line and why is the dynamics one wavy?)
Trajectory Reactivity and Transition State Theory
Several dynamic reaction trajectories were simulated to assess how different internuclear momenta can affect the formation of products from the same starting radii (r1 = 0.74, r2 = 2.0).
| p1 | p2 | Reactive? | Description |
|---|---|---|---|
| -1.25 | -2.50 | ✓ | System crosses saddle point, straightforward formation of products |
| -1.50 | -2.00 | X | Approaching H atom does not carry sufficient momentum to breach transition state saddle |
| -1.50 | -2.50 | ✓ | Approaching H atom has sufficient momentum to cross saddle point, straightforward formation of products |
| -2.5 | -5.0 | X | Strong momenta—approaching Hc atom breaches saddle point, vibrational energy in HB-HA pair sufficient to reverse across saddle point (formation of high energy products -> reformation of reactants) |
| -2.5 | -5.2 | ✓ | Strong momenta—Hc breaches saddle transition, HB-HA pair reverse across saddle, Hc-HA vibrational energy crosses again (three saddle point crossings; formation of high energy products -> reformation of high-energy reactants -> final formation of stable products) |
(Fv611 (talk) 14:41, 9 June 2017 (BST) Could have discussed a bit more)
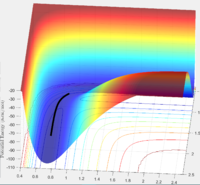
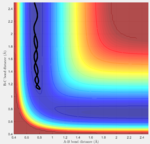
Transition State Theory is a model by which to asses a reaction's progress via the identification of a transition state boundary, or critical dividing surface, along the potential energy surface of a given reaction system[1]. This critical boundary serves to split a reaction surface into exclusive reactant and product "halves". In the case of a simple symmetrical system like H+H2, the critical dividing surface would be a line which starts at the origin of the energy surface and passes through the saddle point (lies somewhere upon the lighter blue surface between valleys), such that it ultimately contains the highest energy points between reactant and product valleys. Intersections of a reaction coordinate with this critical boundary define the transition state for that specific trajectory. A key assumption of transition state theory as it applies to calculating reaction kinetics is that it expects all systems which cross the boundary to ultimately form products.
In the case of the simplest dynamic trajectory simulated for this system (leftmost image), this transition state theory is effective to prescribe the reaction dynamics—the system simply passes the critical boundary and "sinks" into the product valley. However, it can be seen in the final two trajectories, that the original energies supplied to the reaction trajectory are sufficient to cross and recross the critical boundary multiple times, leading to both reactant and product formation respectively. In cases similar to that of the penultimate trajectory, in which the critical boundary can be crossed but reactants ultimately reformed, any rate constants calculated using transition state theory would be skewed higher than those measured experimentally as TST would expect a greater frequency of product formation than actually occurs.
 |
 |
 |
 |
 |
(Fv611 (talk) 14:41, 9 June 2017 (BST) Critically, TST only deals with the reaction coordinate. You could have made this point much clearer.)
Dynamics of the F-H-H System
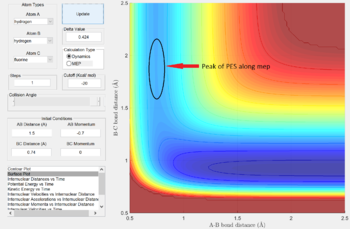
Energetics of Transition
As seen in Fig. 5, the F + H2 system (along the vertical valley on the left of the PES) is a higher energy state (lighter blue) than the HF + H system formed in the lower valley (darker blue). As expected from the stronger bond of HF (568 kJ/mol) to that of H2 (436 kJ/mol), this means that the F + H2 process is exothermic and the inverse H + HF process is endothermic.
(Fv611 (talk) 14:41, 9 June 2017 (BST) Yes, but the argument would have been stronger if you had provide energy values or a side view of the PES rather than pointing out lighter/darker areas.)
In this case, the asymmetrical energies of the reactant/product pair skew the location of the critical transition boundary from what it held earlier. Following Hammond's postulate, by which the transition state most closely resembles the state (reactant or product) to which it is closer in energy, the transition state of the F--H--H system would lie closest to the higher energy F+H2 state. This agrees with the classification of F+H2 as the exothermic direction, as it would pass the transition state early in the reaction coordinate, while the endothermic H+HF direction will pass the transition state late in the coordinate. The general location of this energy saddle is highlighted in Fig. 5 and can be seen to be significantly shifted upwards, towards the F+H2 valley.
Activation Energies
To identify the activation energies in this system, a transition state along the mep was estimated to be situated at r1 = 0.74 (HA-HB bond distance) and r2 = 1.8 (F-HB distance). Further minimal energy pathways from +/- 0.1 angstroms of the r2 F-H distance were simulated to yield a potential energy vs. time plot from which activation energies can be calculated for each reaction. The potential energy/time plot of the H + HF reaction (Fig. 6) yielded an activation energy of 125.9 kJ/mol, while the F + H2 reaction (Fig. 7) was estimated to have an activation energy of 1.26 kJ/mol.
Trajectory Reactivity
F+H2 Reaction
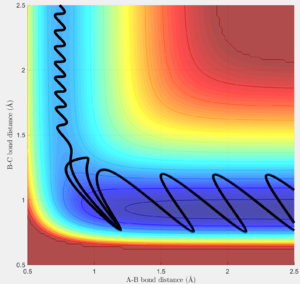
A reactive trajectory of the F+H2 reaction was simulated (rHH = 0.74, pHH = 0; rHF = 2.5, pHF = -1.5). The lesser vibrational energies of reactants (blue oscillations) compared with the products (large red oscillations in Fig. 8 and bond distance oscillations in Fig. 9) is indicative of the exothermic nature of the reaction. This release of potential energy into the product's kinetic vibrational energy is the mechanism by which such an exothermic reaction would release heat in an experimental setting. Such an exothermic gradient might be measured using calorimetry.
(Fv611 (talk) 14:41, 9 June 2017 (BST) Yes, but calorimetry would not pick up whether the energy if vibrational or translational.)
 |
 |
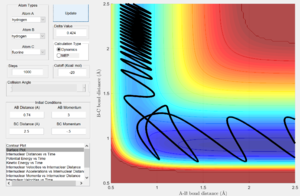
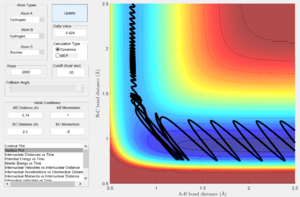
Using the same internuclear distances, a reactive trajectory was established with pHH = 3.0, pHF = -0.5 (Fig. 10). With such a trajectory, significant vibrational energy is held within the H-H bond (as imbued by initial internuclear momenta) at the start of the reaction and the system is gradually pulled through to the H+HF products, less dependent on the translational energy of the approaching fluorine (given by pHF). A significant decrease in the initial H-H bond vibrations (reducing pHH to 0.1, Fig. 11) makes the reaction unsuccessful. From this system, a marginal increase in the translational energy of the approaching fluorine (changing pHF to -0.8, Fig. 12), yields a successful trajectory. The lesser magnitude increase in pHF (translational energy) required to recover reactivity, relative to the decrease in pHH (vibrational energy) which lost reactivity, suggests that the vibrational energy of the H-H bond is not suitably oriented to favor the reaction while the translational energy of the approaching fluorine is efficiently able to induce conversion to products.
 |
 |
 |
H+HF Reaction and Polanyi's Rules
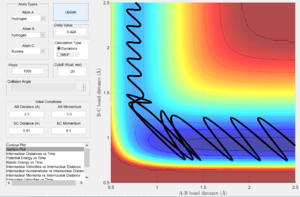
The inverse endothermic reaction of H+HF (Fig. 13), to produce F+H2, required significantly larger momenta to produce a reactive trajectory (rHH = 2.5, rHF = 0.91, pHH = -1.5, pHF = 6.5). This is expected upon changing direction from an exothermic process to an endothermic one.
However, the distribution of initial energy between vibrational and translational states for reactive trajectories in either direction is of interest. Opposite to the case of the exothermic reaction seen above—in which translational energy is most effective at inducing reactivity—the vibrational H-F bond energy is most important in inducing reactivity in this case, the system's endothermic counterpart. These energy distributions are a reflection of Polanyi's rules—a guideline based on empirical evidence that vibrational energy is more effective at promoting endothermic reactions with late-stage transition states than translational energy, and vice versa[2]. In the case of the F+H2 <-> H+HF system, this is indeed seen to be the case.
References
1 I. N. Levine, Physical Chemistry, McGraw-Hill, 2009.
2 J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161-168 (DOI:10.1021/ar50053a001).