MRD:eunicemoon01205028
Molecular Reaction Dynamics
Ng611 (talk) 13:36, 11 May 2018 (BST) consider adding an Introduction section in future reports.
Exercise 1
1.1 Minima and Transition States
There are two minima and one transition state in the potential surface diagram. The minima correspond to stationary points with gradient value of 0. Therefore the minima can be described as a derivative of potential energy over nuclear distance: ∂V/∂r1=0
The transition state is saddle point in the PES. The saddle point is a stationary point which is a maximum point on a minimum energy path. Unlike minima, the saddle point will have a negative curvature value. Therefore the transition states have one component which its second derivative will be less than zero. [1]
Ng611 (talk) 13:38, 11 May 2018 (BST) Good explanation. I would also make it clear that one co-ordinate lies along the MEP whilst the other lies orthoganal to it.
1.2 The Location of Transition state
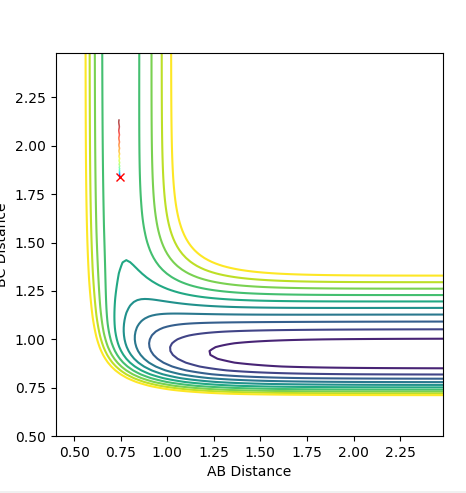
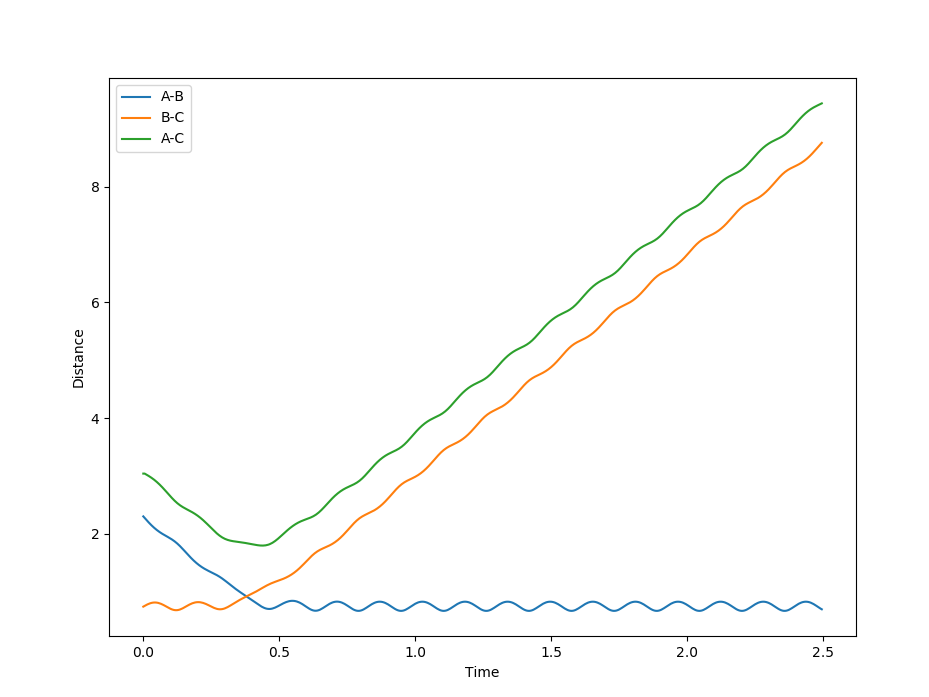
The estimated value for the transition state position is rts=0.906Å.
Ng611 (talk) 13:40, 11 May 2018 (BST) Interesting choice of file name...
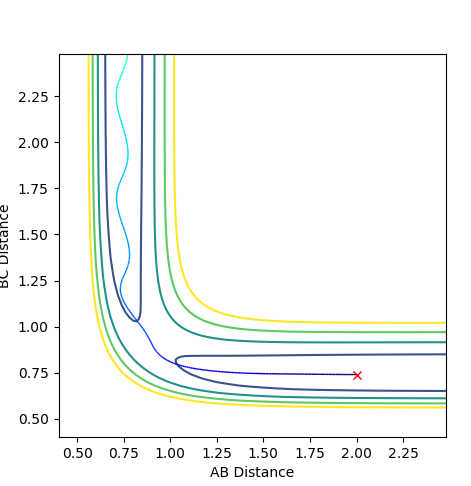
The transition state position is at where the distance A-B and distance B-C are the same. The graph above shows the internuclear distance over time.
Ng611 (talk) 13:40, 11 May 2018 (BST) Did you run a trajectory to confirm that you've actually reached your TS? What about the effect of slight displacements from your estimated TS?
1.3 MEP and Trajectory
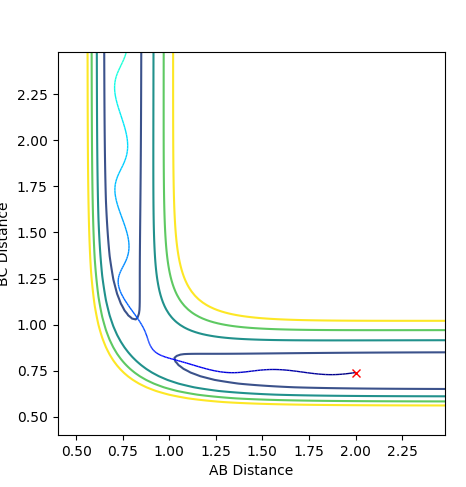
The minimum energy path and the dynamics calculation provides a reaction path from the transition state. The used values for the calculation are: r1=0.916Å , r2=0.906Å, p1=p2=0
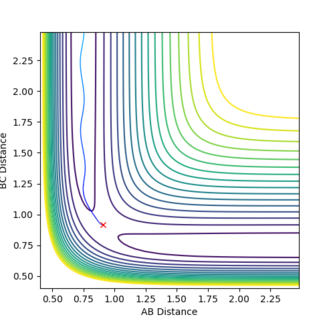

The line starting from a red cross indicates the reaction path. The dynamics plot show reaction starting at the transition state. The reaction path then travels to the product side and goes to completion. Whereas in the MEP plot, the reaction path starts at the transition state but only proceeds a little to the product side. The reaction is not complete in this case.
Ng611 (talk) 13:43, 11 May 2018 (BST) Ok, but is this all that was shown? What are the fundamental differences between dynamics and MEP calculations? Also, if you start from the TS, why does you system react to form products?
1.4 Transition State experimental and assumption
| p1 | ps | Total energy | Reactivity |
|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Reactive |
| -1.5 | -2.0 | -100.456 | Unreactive |
| -1.5 | -2.5 | -98.956 | Reactive |
| -2.5 | -5.0 | -84.956 | Unreactive |
| -2.5 | -5.2 | -83.416 | Reactive |
The trajectory goes through the transition state towards the product. There's weak oscillation after the transition which indicates vibration of the formed A-B molecule.
The trajectory does not go through the transition state but bounces back and continue to oscillate further.
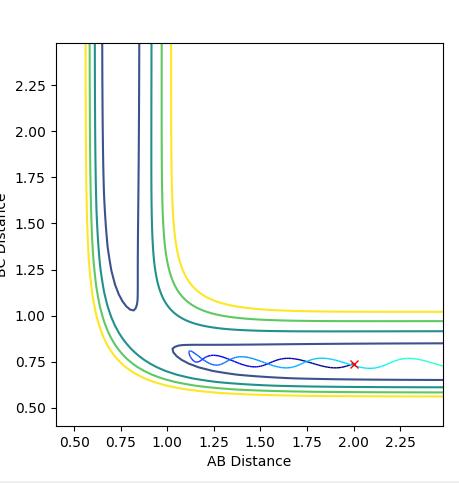
The trajectory goes through the transition state to the product.
The trajectory gets to the transition state but bounces back to the reactants side. There's big oscillation due to the vibrational energy.
The trajectory goes through the transition state and oscillates to the product side.
The original hypothesis which says that in a given bond length, if the momentum is high enough, the reaction will proceed to form products. However, seeing the results from the program it is shown that even in high momentum, some reactions will not form products thus unreactive.
Transition State Theory Assumptions
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The assumptions on the Transition State Theory is derived in calculating the reaction rate using the transition state. The two basic theories are: 1.1 Electronic and nuclear motions are independent of each other 1.2 The reactant molecules follow the Boltzmann distribution
And there are other assumptions which are more specific to the theory is: 2.1 Once the molecular systems that have passed the transition state in the direction of products cannot reform reactants. 2.2 In the transition state, motion along the reaction coordinate is treated classically as a translation and is separated from the other motions. Therefore the possibility of multiple motions thus multiple pathways are ignored. 2.3 The transition states which proceeds to the product follow the Boltzmann distribution, even in the absence of an equilibrium in the reaction. This assumption is known as the quasi-equilibrium hypothesis. [2]
On the other hand, there are few points in the assumptions that make the experimental results defer from the theoretical results.
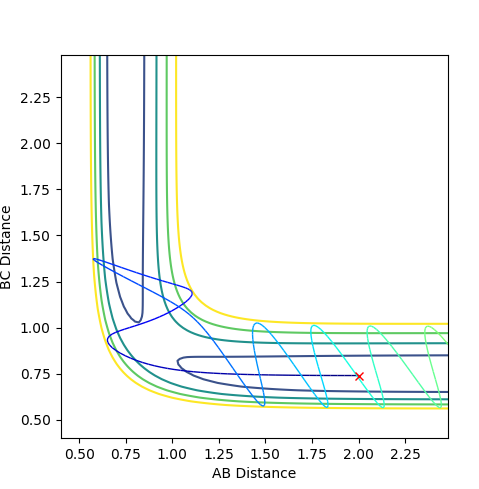
First of all, the assumption 2.1 states that all molecular collision with enough energy to get to the transition state should proceed to products. Bur from the results above, some reactions do cross the activation barrier and make it to the transition state but it recrosses the barrier and comes back to the reactants. The reason for barrier re-crossing, not being able to react in bi-molecular collision, can be due to the collision happening in a wrong orientation. Due to the barrier re-crossing, the reaction mechanism which follows the assumptions A + B → Xǂ → C is in real life close to the reversible reaction: A + B ⇌ Xǂ → C.[3]
Also, assumption 2.2 focuses on the classical behaviour of nuclei, ignoring the quantum mechanical phenomenon. Light molecules such as H and D atoms can tunnel through the activation barrier and from products despite the collision energy not being enough to overcome the barrier.
Therefore, unlike the assumptions which state there's only one pathway, passing the transition state, to reach the products but in reality, the reactants may re-cross the activation barrier and reform products or tunnel through the barrier. As there are different other pathways in real life, the rate of reaction is slower than the rate of reaction assumed by Transition State Theory.
Ng611 (talk) 13:47, 11 May 2018 (BST) Good discussion!
Exercise 2
2.1 PES inspection
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
Locate the approximate position of the transition state.
The reaction F + H2 is exothermic: the products are lower in energy than the reactants. The bond formed in the reaction which is H-F is more stable than the H-H bond. The enthalpy of H-F bond formation is more negative than H-H bond which results in negative reaction enthalpy. The reaction H+HF is endothermic as overall enthalpy of reaction is positive: the dissociation enthalpy of HF is much larger than the H-H bond formation enthalpy.
2.2 Location of the transition state
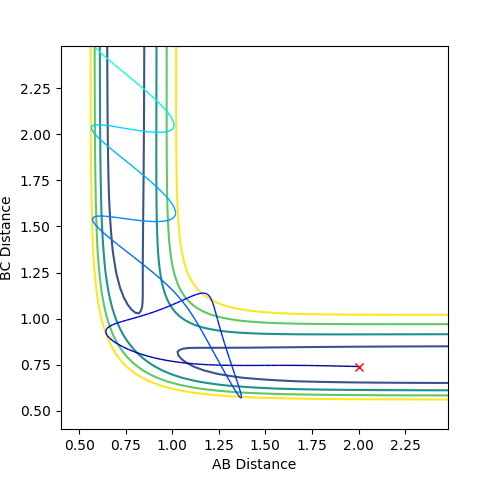
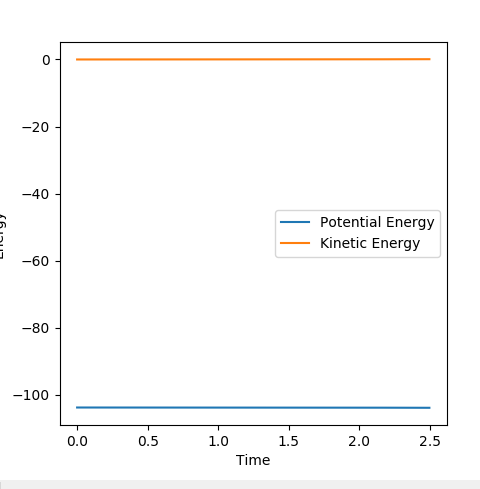
For F + H2: F-H distance= 1.81Å H-H distance=0.746Å
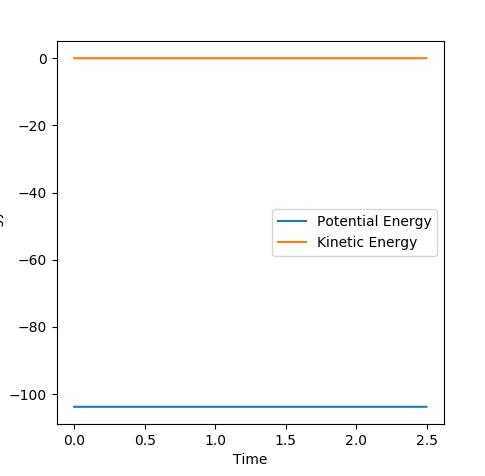
From the diagram below, it can be seen that in the proposed location of the transition state, both the potential energy and kinetic energy are unchanging.
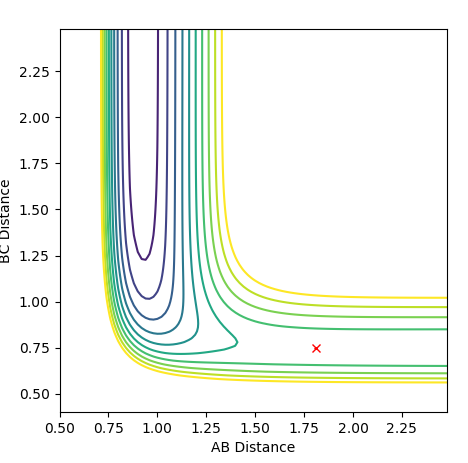
For H + HF: F-H distance= 1.81Å H-H distance= 0.746Å
Ng611 (talk) 13:48, 11 May 2018 (BST) Good! You should have also done something similar with the H + H2 reaction.
And again, the diagram below shows that in the potential energy and kinetic energy are unchanging at the transition state.
Ng611 (talk) 13:48, 11 May 2018 (BST) What are you trying to show with the above figure?
The positions of the transition state for two systems are different as the F + H2 is an exothermic reaction and H+HF is an endothermic reaction. According to the Hammond's postulate, the transition state resembles the closest neighbouring species: for exothermic reaction resembles the reactants and for the endothermic reaction, the transition state resembles the products. (REFERENCE) Ng611 (talk) 13:50, 11 May 2018 (BST) Yes, a reference would have been useful here
2.3 Activation Energy of Reactions
The activation energy for the reaction is the difference in energy in between transition state and the reactants. The activation energy is calculated using the MEP calculation.
| Reaction | Transition State energy | Energy of reactants | Activation Energy |
|---|---|---|---|
| F + H2 | -103.75kJ/mol | -103.99kJ/mol | 0.24kJ/mol |
| H + HF | -103.75kJ/mol | -133.82kJ/mol | 30.07kJ/mol |
2.4 The mechanism of release of the reaction energy
There are initial conditions to result in a reactive trajectory for the F + H2:
F-H distance:2.3 H-H distance:0.76 F-H momentum:-6.9 H-H momentum:-0.9
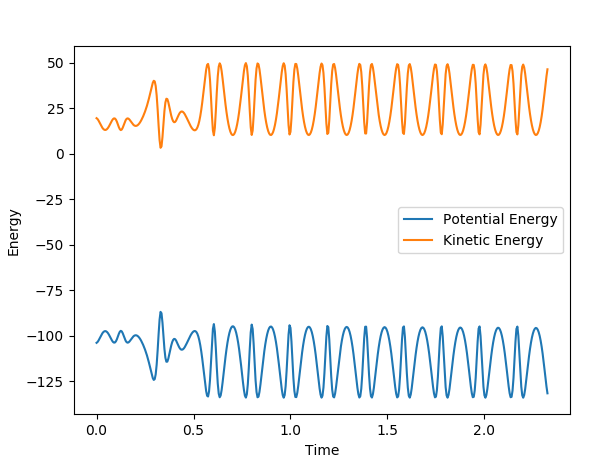
The reaction is exothermic which releases excess energy. This energy causes the H-F bond to vibrate with greater oscillation.
It can be seen that as the potential energy decreases, the kinetic energy increases. This is consistent with the law of conservation of energy which states that the energy is not created nor lost.
The energy transfer can be experimentally measured through calorimetry.
Ng611 (talk) 13:52, 11 May 2018 (BST) Possibly, although calorimetry probably would only measure average kinetic energy and probably wouldn't allow you to determine how much of that comes from vibrations.
2.5 Polanyi's empirical rules
Polanyi's empirical rules suggest that depending on the location of the transition state, either vibrational or translational energy is favoured in activating a reaction. The early transition state favours the transitional energy whereas the later transition state favours vibrational energy.
In the F + H2 system, the reaction is exothermic therefore the transition state is close to the reactants. According to the Polanyi's rule, translational energy is more efficient in activating the reaction than the vibrational energy. For the plots below, the F-H distance used is 2.32 Å and the H-H distance is 0.75 Å. Also, p1 represents vibrational energy whereas p2 represents translational energy.
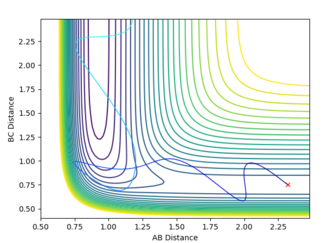
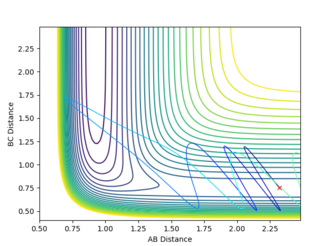
The plots show that in higher translational energy, the reaction path proceeds to completion. But, in lower translational energy, the reaction path bounced back to the reactants side. This corresponds to the Polyani's rule that an exothermic reacti,on the translational energy is more efficient.
On the other hand, the H+HF system is endothermic. This means that there's later transition state and according to the Polanyi's rules vibrational energy will be more efficient in crossing the activational energy barrier. The plots below show the H+HF reaction path in different vibrational energy.
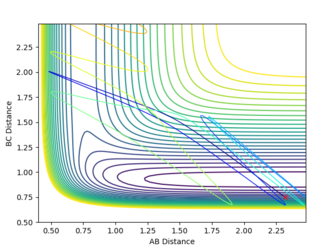
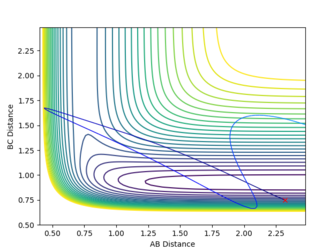
As shown in the plot, when the vibrational energy was higher, the reaction path proceeds to the product but when the translational energy is higher than the vibrational energy the product is not formed. This correlates to the Polanyi's principle.
Ng611 (talk) 13:53, 11 May 2018 (BST) Good discussion here.