MRD:et2118
Molecular Reaction Dynamics: Applications to Triatomic Systems
The reactivity of triatomic systems where an atom and a diatomic molecule collide in a linear configuration in the gas phase can be studied and predicted using molecular dynamics trajectories. A chemical reaction can be represented through the relative motion of atoms during the reaction which varies due to differing interatomic interactions at each position, approximating that the atoms obey classical mechanics and neglecting the quantisation of molecular vibrations and quantum tunnelling effects.
Exercise 1: H + H2 System
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The progress of a chemical reaction can be represented by a potential energy surface as a function of interatomic distances. Mathematically, the transition state is defined as the saddle point on the multivariate potential energy surface; the maximum of the minimum energy path valley along the potential energy surface linking the reactants and products. More generally, it is the maximum along one direction but also the minimum in the orthogonal direction.The stationary point at which the transition state is present has a partial derivative with respect to interatomic distances equal to zero, where the metaphorical rolling sphere would be stationary at the top of the hill. Changing the geometry even slightly and moving away from the transition state in the direction of either the reactants or products results in a decrease in the potential energy along the series of local minima, the minimum energy path, towards that respective direction.
One can locate the transition state by testing trajectories near the transition state to see if they result in movement away from the starting point despite initially having zero momentum, and using interval bisection to narrow down the point where there is no movement of the trajectory. At this point, since the negative of the first derivative of the potential energy surface with respect to an interatomic coordinate gives the force, the transition state has zero force on the atoms in both directions. This means the transition state can be identified by inputting values that bring the values of the forces as close to zero as possible.
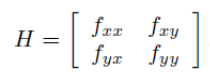
One can use a Hessian matrix to distinguish between the local minima and the saddle point where the transition state exists. If fxx is greater than zero and the determinant of the matrix is greater than zero, the point is a local minimum. If fxx is less than zero and the determinant of the matrix is greater than zero, the point is a local maximum. If the determinant of the matrix is less than zero, the point is a saddle point. [1]
Great, well defined and explained. The second derivative is also a mathematical part of the definition. Rs6817 (talk) 16:55, 27 May 2020 (BST)
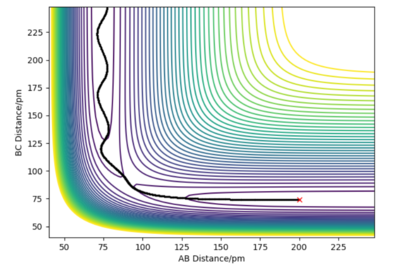
Report your best estimate of the transition state position and explain your reasoning illustrating it with a "internuclear distances vs time" plot for a relevant trajectory.
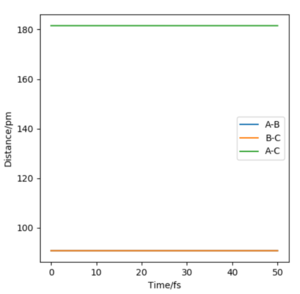
In the case of the hydrogen atom colliding with the hydrogen molecule, the potential energy surface is symmetrical so the interatomic distances must be the same at the transition state and starting a trajectory at this distance should result in a zero gradient orthogonal to the ridge of the trajectory. This trajectory will oscillate perpendicular to the minimum energy path valley, locating the transition state geometry.
A transition state position of rab = rbc = 90.775 pm is the best estimate of the transition state position where the forces acting on the atoms are zero.
In the internuclear distances vs time plot, the two interatomic distances do not oscillate and do not increase or decrease, giving straight lines showing the transition state geometry where the trajectory sits at the saddle point. There is no explicitly visible blue line because the orange line and blue line are at the same interatomic distance. This is the best approximation of the transition state position since there are no oscillations.
Ok, but I think you could have utilised a few other trajectories to illustrate your point. Make sure to refer to your figures in the text, i.e. 'Looking at figure X shows y' where each figure is numbered by their appearance in the text Rs6817 (talk) 16:55, 27 May 2020 (BST)
Comment on how the mep and the trajectory you just calculated differ.
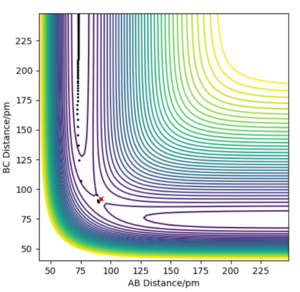
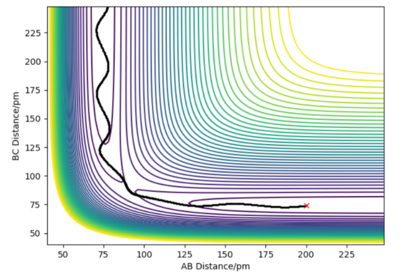
The minimum energy potential (mep) calculation corresponds to infinitely slow motion, disregarding inertial motion, resetting the momentum that would be gathered when going down the potential energy surface to zero at each point in time. This results in the atoms having no momentum and no oscillation in the diagram. Instead the trajectory is a straight line following the minimum energy pathway, resulting in no vibration in the hydrogen molecule, simply translational energy in the hydrogen atom moving away from the hydrogen molecule which is unphysical.
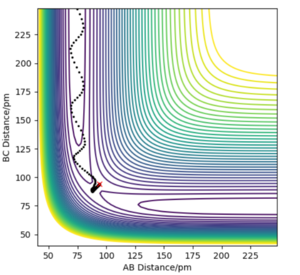
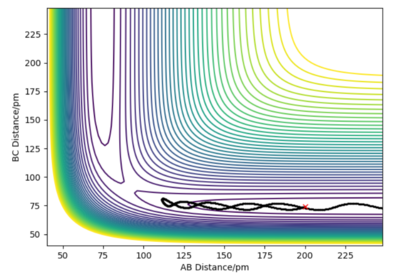
The dynamics simulation depicts a more realistic trajectory for the system to take however, as it considers the inertial motions, resulting in a wavy trajectory where the hydrogen molecule vibrates. Going down the potential energy surface gathers momentum, and the system has both translational and vibrational energy.
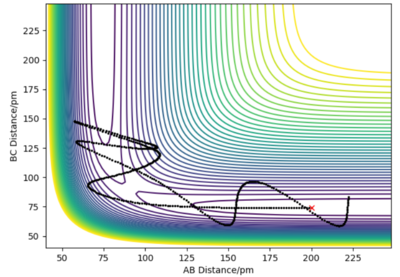
Complete the table by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Reactive | The hydrogen atom collides with the non-vibrating hydrogen molecule and forms the products, leaving the new hydrogen atom moving away from the new vibrating hydrogen molecule. | 
|
| -3.1 | -4.1 | -420.077 | Unreactive | The hydrogen atom collides with the vibrating hydrogen molecule but does not react because the activation barrier is higher than the energy of the system, resulting in the hydrogen atom moving away from the vibrating hydrogen molecule. | 
|
| -3.1 | -5.1 | -413.977 | Reactive | The hydrogen atom collides with the slightly vibrating hydrogen molecule and forms the products. | 
|
| -5.1 | -10.1 | -357.277 | Unreactive | The hydrogen atom collides with the non-vibrating hydrogen molecule forming the product with a vibrating hydrogen molecule. However, the trajectory crosses back over the transition state and reforms the products, with the hydrogen molecule now vibrating. | 
|
| -5.1 | -10.6 | -349.477 | Reactive | The hydrogen atom collides with the non-vibrating hydrogen molecule, forming the products, with a vibrating hydrogen molecule. The trajectory crosses over the transition state towards the reactants before finally crossing back over to form the products, with a strongly vibrating hydrogen molecule formed. | 
|
From the table, one can conclude that changing the momenta even slightly will have a significant impact whether or not the reaction goes to completion. The completion of the reaction however is not dependent solely on the total energy of the system since one can see that there is no relation between the total energy and the reactivity. Instead, varying the momenta has an impact on the reactivity, especially favouring larger differences in momenta.
Ok, your table is well structured and your conclusion mostly clear. Total energy does show a relation but what does it say about the type of energy? Rs6817 (talk) 16:55, 27 May 2020 (BST)
Given the results that you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Overall the Transition State Theory overpredicts the reaction rate values compared to the experimental reaction rate values. Transition State Theory assumes that there is no barrier recrossing where the system reverts back to the reactants and instead assumes that when the trajectory passes through the transition state and forms the products, the products do not cross the transition state again and only one crossing of the transition state is allowed. This means that the theory predicts more product to be made than there actually is since the trajectory can cross back over as seen in the previous example, resulting in an overestimate of the reaction rate as the rate of reaction can be approximated by the rate of the reactants passing through the transition state. A smaller and less significant assumption is also that quantum tunnelling is ignored, which does not have as much of an impact for systems with a larger mass since they can be well represented classically, but it does mean that the rate is underestimated since the theory cannot represent the quantum interpretation of the system.[2]
Ok, good description of the assumptions, it would be good to include the reference at the bottom, there is instructions for this in the report guidelines. How do these assumptions directly relate to your results in the above table? Rs6817 (talk) 16:55, 27 May 2020 (BST)
Exercise 2: F - H - H System
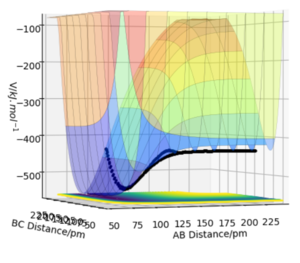
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 system is exothermic since there is a substantial drop in the potential energy surface past the transition state, where the transition state resembles the reactants giving an early transition state.[3] This drop is due to the fact that the H-F bond formed has a high electronegativity difference, resulting in a strong ionic bond. This strong bond has a higher dissociation energy compared to the covalent hydrogen molecule bond and therefore results in a lower potential energy.[4] Conversely, the H + HF is endothermic with a late transition state that resembles the products formed since the bond dissociation of HF requires much more energy.
Ok, stating this is Hammonds postulate would help. Rs6817 (talk) 16:55, 27 May 2020 (BST)
Locate the approximate position of the transition state.
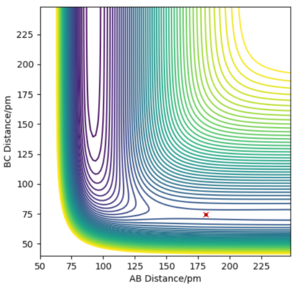
The transition state distance is estimated to be 181 pm between F and H, and 74.49 pm between H and H. This was obtained by predicting that the transition state would resemble the F + H2 system and adjusting the initial conditions for the forces along the atoms to equal zero.
Ok, refernece to figures would aid you here. Rs6817 (talk) 16:55, 27 May 2020 (BST)
Report the activation energy for both reactions.
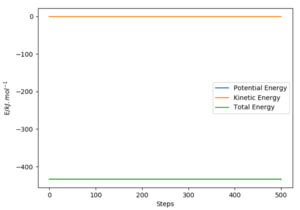
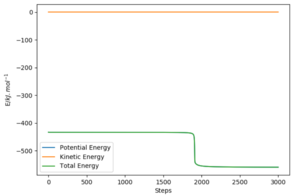
The activation energy can be calculated by employing the mep calculation and bringing up the energy vs time graph for a point slightly off the transition state towards either the reactants or products. The initial state energy value can be subtracted from the transition state energy value in order to obtain the activation energy.
| Reaction | Transition state energy / kJ mol-1 | Initial state energy / kJ mol-1 | Activation energy / kJ mol-1 |
|---|---|---|---|
| F + H2 | -433.981 | -433.932 | 0.049 |
| H + HF | -433.981 | -559.841 | 125.86 |
Good calculation. Rs6817 (talk) 16:55, 27 May 2020 (BST)
In light of the fact that energy is conserved, discuss the mechanism of the release of the reaction energy. Explain how this could be confirmed experimentally.
Since energy is conserved, the total energy must remain constant and energy will be exchanged between kinetic and potential energy. With an exothermic reaction where potential energy is lost, this same amount of energy must be gained through kinetic energy, exhibited in the increase in vibrational energy. The changes in temperature can be observed experimentally through calorimetry however this cannot distinguish between vibrational and translational energy. Instead one would use IR spectroscopy to observe the presence of overtones if there were increased vibrational energy.[5]
Ok, some details fo the expiments or how the energy is distirbuted would be useful. Rs6817 (talk) 16:55, 27 May 2020 (BST)
Discuss how the distribution of energy between different modes (translation and vibration) affects the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's rules dictate that for an early transition state, it is more efficient to invest translational energy in the system as opposed to vibrational energy because it means that the distance between the reactants can become close enough in such a way that the transition state can be reached and the reaction can go to completion. Investing vibrational energy will not allow the reactants to reach an intermolecular distance that corresponds to the transition state being able to form. For a late transition state closer to the products, it is more efficient to have more vibrational energy compared to translational energy because the reaction can only proceed if there is a bigger change in distance between the atoms in the molecule corresponding to the ability to form the transition state. If mainly translational energy were invested, the reactants would move across the reaction coordinate but they would not be able to reach an intermolecular distance corresponding to the transition state.[6]
Ok, true but how does this relate to the system? You can explore the relative contirbutions of vibrational and translational energies. Rs6817 (talk) 16:55, 27 May 2020 (BST)