MRD:es4215may18
Molecular reaction dynamics
Abstract
Calculation of trajectories of reactions involved in H-H-H and F-H-H systems. The systems were analysed for: the activation energy barrier; position and geometry of transition state; and initial conditions needed for successful reaction trajectories. An analysis was made of the suitability of transition state theory to model the reaction dynamics of such systems. good, nice to have an overview--Sw2711 (talk) 10:33, 11 May 2018 (BST)
Background
Transition state theory is often used to model reaction dynamics. In transition state theory, reactions proceed along the minimum energy path between reactions and products. On a potential energy surface, on the minimum energy path the potential energy does not change with respect to small changes in the distance between the atoms deemed to be bonded. The transition state is the highest energy state which must be achieved for the reaction to progress along the minimum energy path. It is a maximum point on this minimum path: it is a saddle point on the potential energy surface. As a result, at transition state, all gradients are zero. Good attempt, I agree with you at TS, all gradients are zero. But you need to tell me, how this differ from a local minimum, of which all gradients are zero too. Then you need to look at the second partial derivative. --Sw2711 (talk) 10:33, 11 May 2018 (BST)
Results and Discussion
H-H-H
A system was simulated of an H atom (A) colliding with H2 (BC) to form another molecule of H2 and a free hydrogen atom. The potential energy surface of the system was symmetrical, so there is no net change in energy associated with this reaction. Since at the point of the transition state, all gradients are zero, if a system is at transition state with all momenta zero it will not move. This principle was used to calculate each H-H distance in the transition state.The transition state distance was calculated as 0.90774 Å to 5 dp.
Really amazing attempt to get 5 dp! But still, your definition of TS is still not quite clear. If the system is at local minimum or maximum, the gradients are all zero too and it does not move--Sw2711 (talk) 10:34, 11 May 2018 (BST)
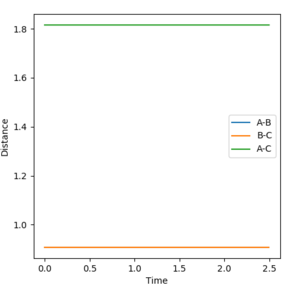
The minimum energy path (MEP) calculation ignores both the bond vibration momentum and the translational momenta of the two molecules. It can thus be used to predict the path a reaction will take. Calculating internuclear distance versus time with initial A-B distance just more than at transition state, the reaction rolls slowly back to reactants.
You are right, MEP ignores the momenta, but it does not really predict the path. It is more to look at the gradient of the energy surface. More like place a ball steadily at a hill, see which way the ball will roll. Try the first example (r1 = 0.74, r2 = 2.3, p1 = 0, p2 = -2.7) and compare using MEP and dynamics, you will see what I mean.--Sw2711 (talk) 10:39, 11 May 2018 (BST)

If the MEP is calculated with initial A-B distance just less than at transition state, the reaction proceeds to products.

The MEP calculation differs from the dynamic calculation in that it does not take into account momentum gained over the course of the reaction. As a result, the dynamic calculation is more useful in calculating the actual reaction trajectory.
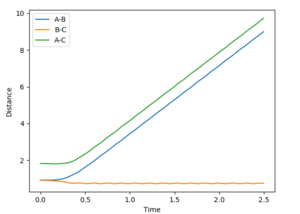

Note that in the MEP calculation it takes longer for the new bond to form. The dynamic calculation also shows oscillation of the new bond formed, which is absent in the MEP.
The following trajectories were calculated. In all cases the AB distance was 2 Å and BC distance 0.74 Å:
| Reaction | BC (vibrational) momentum | AB (translational) momentum | Total Energy | Reactive? |
|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -99.018 | Yes |
| 2 | -1.5 | -2.0 | -100.456 | No |
| 3 | -1.5 | -2.5 | -98.956 | Yes |
| 4 | -2.5 | -5.0 | -84.956 | No |
| 5 | -2.5 | -5.2 | -83.416 | Yes |
Reaction 1 goes ahead in the normal fashion. The particles come together, the transition state is crossed once, and products are formed.
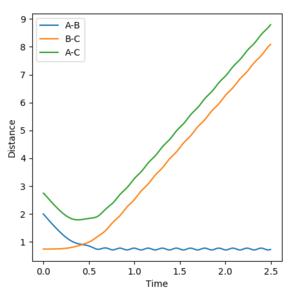
In Reaction 2, the particles do not get close enough to react. There is not enough AB momentum to overcome the activation energy barrier.
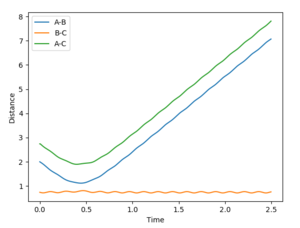
Reaction 3 goes ahead in the normal fashion.

Reaction 4 goes ahead initially, but the reaction then proceeds backwards, crossing the transition state again, leaving the reactants.
recrossing the TS--Sw2711 (talk) 10:39, 11 May 2018 (BST)

Reaction 5 crosses the transition state three times, and so overall the reaction goes ahead.
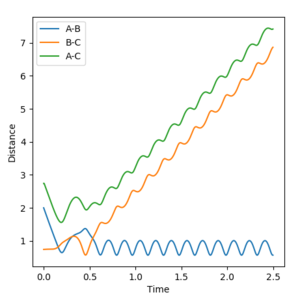
Note that in Reactions 4 and 5, a major assumption of transition state theory is disproved. Transition state theory assumes that the particles behave classically, and that the transition state is the 'point of no return' - once a reaction has proceeded past the transition state it cannot recross. According to transition state theory, the transition state is like a potential energy 'hill' that the reaction must overcome in order to proceed. However, in Reactions 4 and 5, the particles bounce around in the transition state region, crossing the transition state several times before emerging on the reactant or product side. The direction the reaction progresses in is heavily dependent on the initial momenta. Since transition state theory assumes the barrier can only be crossed once, and the dynamic calculations allow for multiple recrossings, experimental reaction rates would be slower than those calculated by transition state theory because transition state theory does not account for reaction trajectories that cross the transition state but then recross back to reactants. Good observation--Sw2711 (talk) 10:39, 11 May 2018 (BST)
F-H-H
The second system simulated was a reaction between a fluorine atom (A) and a molecule of H2 (BC). The potential energy surface of the F-H-H system was asymmetrical. The system is lowest in energy when F-H is bonded. Therefore, the reaction between F and H2 is exothermic, whilst the reverse reaction is endothermic. Consequently, the H-F bond is stronger than the H-H bond.I need some evidence here.--Sw2711 (talk) 10:57, 11 May 2018 (BST)
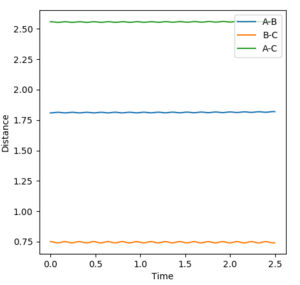
The transition state occurs when the H-H distance is approximately 0.75 Å and the F-H distance is approximately 1.809 Å. Note that the H-H distance is very close to the typical H-H bond distance. This agrees with Hammond's postulate as the reaction is themodynamically very in favour of the formation of the H-F bond. The F+H2 reaction will be referred to henceforth as the forward reaction and the H+HF reaction the backward reaction.
Good--Sw2711 (talk) 10:57, 11 May 2018 (BST)
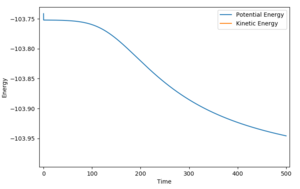
The activation energy for the F+H2 reaction is +0.2 kcal/mol. This is shown in the potential energy versus time graph of the MEP calculation starting with the F-H distance just more than at transition state and zero momentum, in which the reaction trajectory rolls gradually back to the reactant side.
The same method was used to calculate the activation energy of the H+HF reaction. This was calculated as +30 kcal/mol.
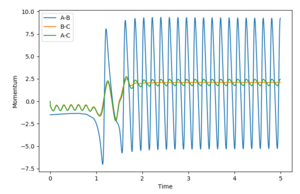
A reaction trajectory for F+H2 with initial conditions bond distance 0.74 Å and H-F distance 2.25 Å, H-H momentum -0.5 and F-H momentum -1.5, is successful. The H-F bond vigorously oscillates in the product. This absorbs the energy released by the drop in potential energy caused by the H-F bond formation.I think you are missing some questions here? ‘In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy How could this be confirmed experimentally?’ --Sw2711 (talk) 10:57, 11 May 2018 (BST)
With F-H momentum at -0.5, and the energy of the system predominantly from H-H bond vibration, reactions are generally not observed. The increased H-H momentum makes the reaction bounce around considerably in the transition state area but the F-H momentum is not large enough to push it over to the product side. When the F-H momentum was increased slightly and H-H momentum decreased, the reaction went ahead.
In the reverse direction, reaction went ahead with H-F vibrational momentum of 8.5 and H-H translational momentum of -0.45. It appears that in an endothermic reaction with a late transition state, a large bond vibrational momentum increases the efficacy of the reaction as a smaller translational energy decreases the chance of recrossing. In an exothermic reaction, with an early transition state, large bond vibrational energy increases the chance of recrossing.
Good observation and summary. Small comment for general report guidance - There are a lot of information in these two sentences. It is also nice that you’ve given a figure (large vibration, reaction efficacy increase, late TS) to support your conclusion. It would be nice to use a few more figures to support. E.g. (small translational energy, chance of recrossing decreases. Late TS) and (large vibrational energy, change of recrossing increases, early TS). --Sw2711 (talk) 10:57, 11 May 2018 (BST)

Conclusion
Transition state theory is a powerful simplification for the dynamics of complex reactions. However, actual reaction dynamics are far more complex. Computational models are useful for calculation of actual reaction dynamics. They can provide a window into the exact conditions needed for a reaction to successfully cross the transition state barrier and illustrate why the distribution of energy in a system between vibration and rotation is crucial to the success of a collision.
The investigation could be extended to include all X-H-H systems (where X is a halogen) and to establish trends down the group regarding activation energies and transition state positions with regards to H-H and H-X bond lengths. This could be used to predict successful reaction trajectories for these reactions.