MRD:dt2315
Molecular Reaction Dynamics of a H + H2 system
Potential energy surface gradient
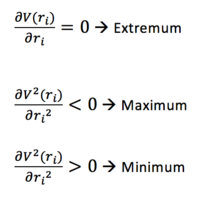
An extremum point (i.e. maximum or minimum) occurs when the gradient is 0.
In order to distinguish between the two, the second derivative needs to be taken. If this is positive, the point is a minimum and the total potential energy surface can be identified. If this is negative, the point is a maximum and can be identified as a transition state, defined as the maximum on the minimum energy path.
Note: the derivatives need to be taken with respect to both bond stretching displacements (i.e. i = 1, 2).
(In your picture you are using the ith coordinate, but in your text you are using only one coordinate. What about a transition state with more than one coordinate (such as in this exercise)? Tam10 (talk) 11:06, 1 June 2017 (BST))
Transition state position
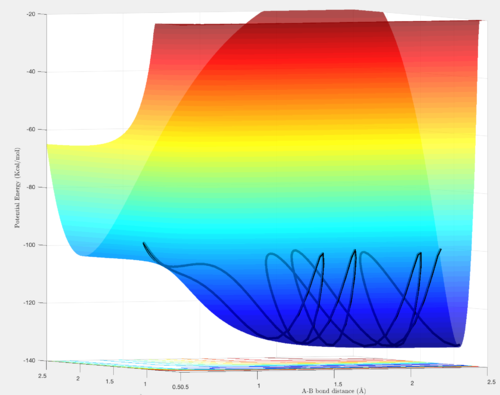
For a H + H2 system the potential energy surface is symmetric as only one type of atom is present. The transition state occurs when the the internuclear distances are equal (i.e. r1 = r2), meaning the extent of formation of the new bond is the same as the breaking of the other bond. At this instant in time, the particles are stationary and are at a local minimum.
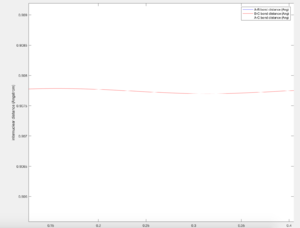
For an internuclear distance of 0.9077 A, the plot of internuclear distances over time shows the distances between atoms stay constant. A zoomed in capture shows that there still are some small oscillations and the precision could be further increased. However, the estimation to 4 decimal places seems reasonable.

Minimum energy path (mep)
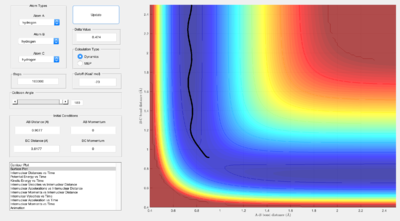
The minimum energy path (mep) corresponds to infinitely slow motion, particles following the path along the foot of the potential energy surface valley. The point where the line stops in the captures presented is a saddle point and corresponds to the transition state internuclear distance.
The mep, unlike the dynamic trajectory, does not show any oscillations and only follows the valley floor.
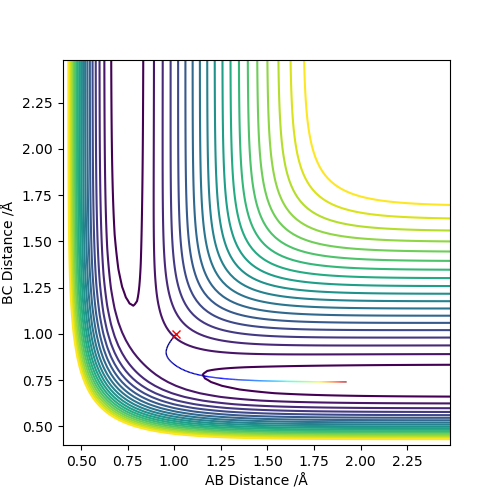
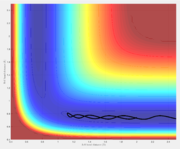
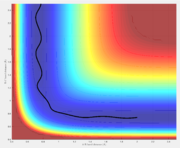
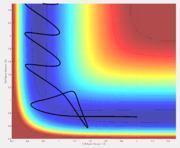
Reactive and unreactive trajectories
A reactive trajectory is one in which the reactants are successfully converted into products. The distribution of translational and vibrational energy determines the result and five cases are described below. The following trajectories were calculated for r1 = 0.74 and r2 = 2.0
| p1 | p2 | Trajectory | Description |
|---|---|---|---|
| -1.25 | -2.5 | Reactive | A approaches the BC molecule on the minimum energy path (mep); after the collision, the vibrational energy increases |
| -1.5 | -2.0 | Unreactive | A approaches with insufficient translational energy |
| -1.5 | -2.5 | Reactive | A approaches a vibrating BC molecule; after the collision, the vibrational energy increases |
| -2.5 | -5.0 | Unreactive | A approaches with enough translational energy but the wrong phase of vibrational energy |
| -2.5 | -5.2 | Reactive | A approaches with enough translational energy and vibrational energy to eventually lead to bonding; it should be noted A first bounces back and only approaches successfully afterward |
(There is no vibrational energy in the 4th example. Tam10 (talk) 11:06, 1 June 2017 (BST))
 |
 |
 |
 |
 |
Transition State Theory
The transition state theory (TST) or the activated-complex theory (ACT) is a simplified model that enables the calculation of reaction rates. TST only requires potential energy surface calculations in the regions of reactants, products and transition state, without requiring trajectory calculations. The theory assumes all molecules that pass over the energy barrier given by the transition state, a saddle point on the potential energy surface, will turn into products. This is reasonable for most cases, unless the energy barrier is very low, in which case the classical approach becomes insufficient and a quantum tunnelling effect should be considered. The second assumption is that during the reaction, the energy of the reactants maintains a Boltzmann distribution. This breaks when the intermediate is short-lived, however. The third assumption is that the Boltzmann distribution of energy of these molecules crossing the energy barrier corresponds to the temperature of the system. 1
Transition state theory can be used to give a qualitative understanding of how chemical reactions take place, yet the predictions for reaction rates are usually not very accurate. It has been seen how although in the products region, the approach can still be unsuccessful so it is expected that not all the collisions are successful even though they have enough energy. Consequently, the prediction rates are expected to be higher than the experimental ones.
Molecular Reaction Dynamics of a F - H - H system
Reaction energetics and bond strength
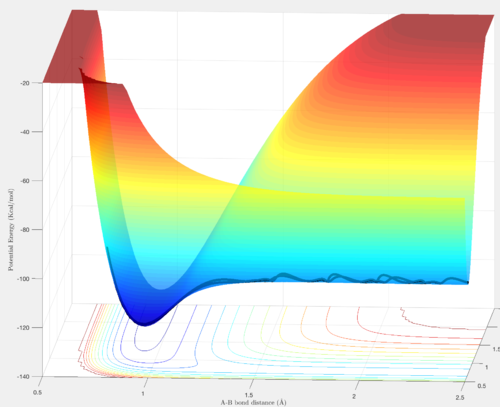
F + H2
By comparing the energies between reactants and products, it can be seen that the products are lower in energy than reactants and the reaction is therefore exothermic.
H + HF
For this process, the products are higher in energy than the reactants, showing the reaction is endothermic. Indeed, if one of the forward reactions is exothermic, the other must be endothermic as it describes the reverse process.
By comparing the energies of reactants and products, insight into the bond strength is provided. Consequently, the H - F bond is stronger than the H - H bond since the energy of the H + HF system is much larger than the energy of the F + HH system, as shown above.
Transition state
According to Hammond's postulate, for an exothermic reaction the early transition state will resemble the reactants (i.e. H2 molecule) and it is hence expected that r2 will be similar to the usual 0.74A bond length. Similarly, for the endothermic reaction, the late transition state will resemble the products, the same H2 molecule.
As the reaction is only the reverse, the transition state is the same and was found at r1 = 1.808A and r2 = 0.745A. For this reaction, the transition state is no longer symmetric.

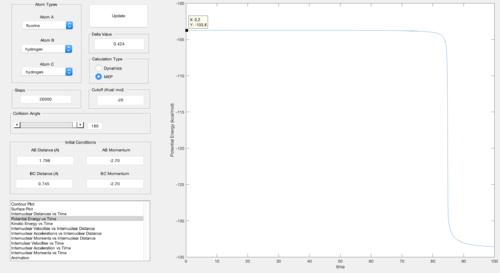
The energy of the transition state (ETS = - 103.8 kcal/mol) was found by plotting the potential energy versus time, the transition state corresponding to the maximum energy.
Activation energies
F + H2
ETS = - 103.8 kcal/mol
ER = - 103.9 kcal/mol
Ea = 0.1 kcal/mol
(This value is a bit low. The reactants weren't converged enough Tam10 (talk) 11:06, 1 June 2017 (BST))
A relatively small value is expected as the transition state resembles the reactants for an exothermic reaction.
By plotting a mep Potential energy vs. time plot at small displacements from the transition state internuclear distance, the energy of the products was found, in this case H + HF. This value was used to find the activation energy of the reverse process, where H and HF represent the reactants.

H + HF
ETS = - 103.8 kcal/mol
ER = - 133.9 kcal/mol
Ea = 30.1 kcal/mol]
This is much larger than the activation energy for the previous reaction and confirms the fact that it is an endothermic reaction. Moreover, the lower energy of the reactants confirms the fact that the H -F bond is stronger than the H - H bond.
Release of reaction energy
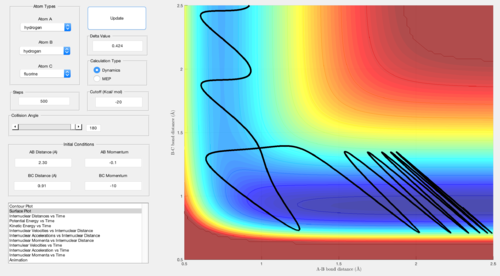
A set of conditions resulting in a reactive approach was identified for the exothermic process by choosing a negative AB momentum and positive BC momentum. This means that when F approaches the H that has to detach, the H that will detach is favourably already going away from the H that will bond to F.
Considering this process is exothermic, the energy gained is released as heat and the results can be confirmed with a calorimetry experiment. Another experiment that can be done is recording the IR spectrum, yet calorimetry would be an easier option in this case.

(Far too much kinetic energy in the reactants. (~43kcal/mol) You should start with a much smaller amount considering your value for the barrier is less than 1kcal/mol Tam10 (talk) 11:06, 1 June 2017 (BST))
Energy Distribution and Polanyi's Rules
Polanyi's empirical rules state that vibrational energy is more efficient than translational energy in promoting a late transition state reaction (e.g. endothermic), whereas the reverse is true for an early-barrier reaction (e.g. exothermic).2 Although they can provide useful guidance, there are situations in which these are not obeyed.
F + H2
For the exothermic reaction, it can be noticed that a although a large vibrational energy is not able to promote the reaction (i.e. large BC momentum), relatively small translational energy (i.e. AB momentum) and small vibrational energy lead to a successful reaction.
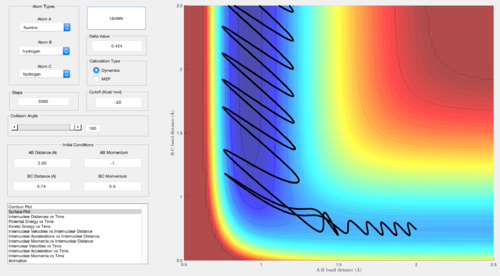
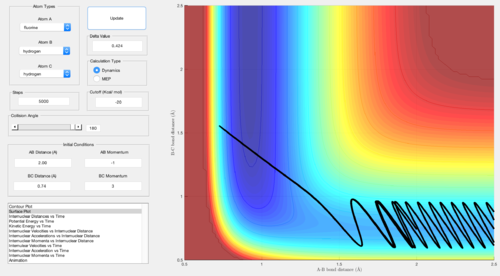
H + HF
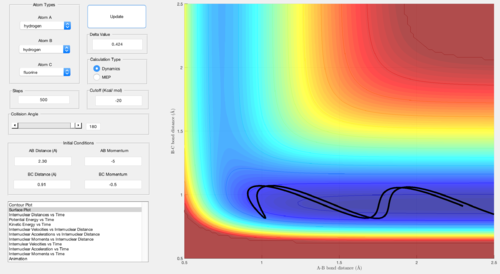
For the endothermic late-barrier reaction, the opposite is true. Very large vibrational energy leads to a reactive approach, whereas although large, translational energy leads to an unreactive approach. However, for an even larger translational energy, the reaction is successful.

References
1. Levine, I. Physical chemistry (6th ed., International ed.), London McGraw-Hill Higher Education, 2009.
2. Polanyi, J. C.Concepts in Reaction DynamicsAcc. Chem. Res. 5, 161–168, 1972.
