MRD:dmd216 01198401
Molecular Reaction Dynamics
H + H2
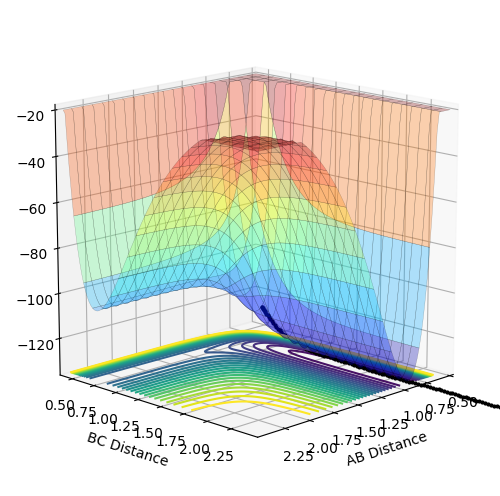
What value do the different components of the gradient of the potential energy surface have at the minimum and at a transition structure? Briefly explain how minima and transition states can be distinguished using the curvature of the potential energy surface.
At the minimum of a potential energy surface, the gradient will be ∂V(ri)/∂ri=0. (This is not true. ∂V(ri)/∂ri>0 Fjs113 (talk) 14:12, 28 May 2018 (BST))
At a transition structure, the gradient of the potential energy surface will be ∂V(r1)/∂r1=0 and ∂V(r2)/∂r2=0. These two second partial derivatives depend on the reaction direction.
Minima are found when ∂2V(ri)/∂2ri=0. The transition state is defined as the maximum on the minimum energy path linking reactants and the products. It can be found when the gradients are 0 and ∂2V(r1)/∂2r1>0 and ∂2V(r2)/∂2r2>0 i.e. a saddle point.
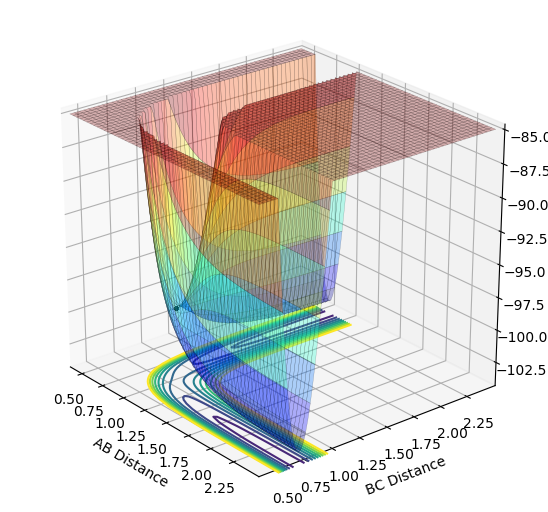
Report your best estimate of the transition state position (rts and explain your reasoning illustrating it with a 'Internuclear distances vs Time' plot for a relevant trajectory.
The best estimate of the transition state position was 0.908Å. This was determined by varying inter-nuclear distances using dynamics calculations. There was a period of no oscillation which is found at the transition state positon so 0.908Å was a good estimate which showed this as shown below.
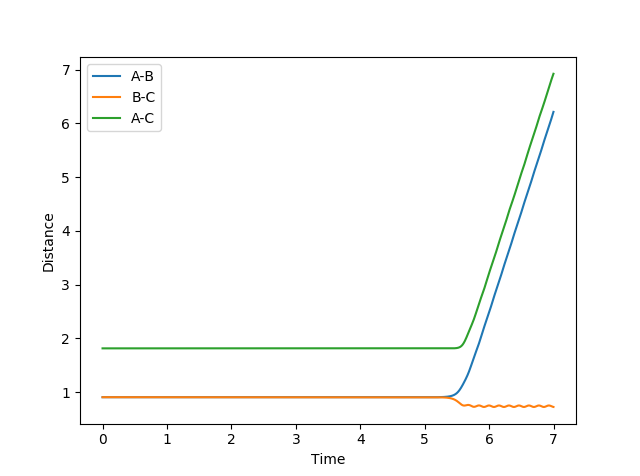
When a trajectory with no initial momentum is started at the transition state where ∂V(ri)/∂ri=0 and dpi/dt=0 and hence the trajectory will remain there forever. As seen in the above graph, the inter-nuclear distance does not change for ~ 5 seconds and the trajectory is a point at the transition state but then suddenly the inter-nuclear distances begin to increase. This is due to the trajectory changing slightly either in the products or reactants direction, resulting in a molecule of hydrogen (B-C) being produced as shown by the oscillation in the above figure. The hydrogen atom A is produced which moves in the opposite direction to B-C, causing increases in A-C and A-B distances.
(Good explanation. Fjs113 (talk) 14:12, 28 May 2018 (BST))
| Angle 1 | Angle 2 |
|---|---|
 |
|
Comment on how the mep and the trajectory you just calculated differ
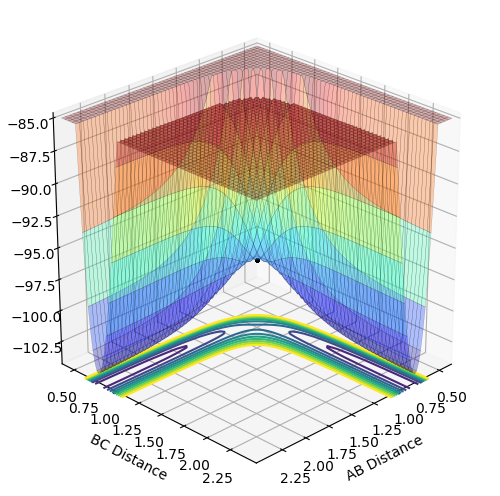
The minimum energy path (mep) is a specific trajectory that corresponds to infinitely slow motion - at each time step, the velocity always resets to zero. The initial conditions for mep and dynamics were setting p1=p2=0, r1=ts+0.01 and p2=Pts. (What do you mean by this last equation? Fjs113 (talk) 14:12, 28 May 2018 (BST))
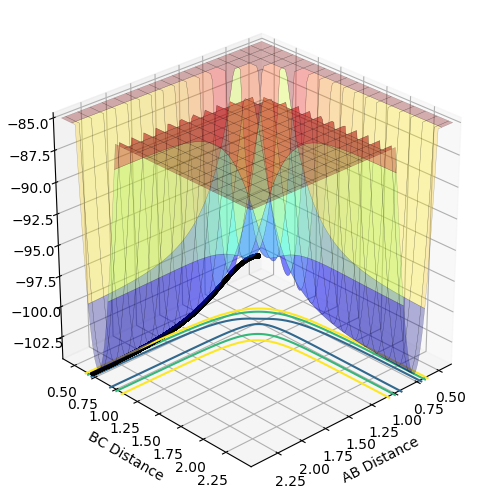
Mep is useful for characterising chemical reactions but does not provide a realistic account of the motion of atoms during the reaction. This is apparent in the below table. Oscillation is shown in dynamics calculations but not in mep calculations as in mep calculations, the velocity is reset to zero along the minima of the surface. In dynamics calculations, the pathway of minimum energy is followed. Oscillations are expected from the formation of a hydrogen molecule so dynamics is better for realistic results.
The below table includes surface plots but also contour plots to emphasise the oscillations shown in the dynamics calculations.
| Dynamics | MEP |
|---|---|
 |
|
| Surface plot A | Surface plot B |
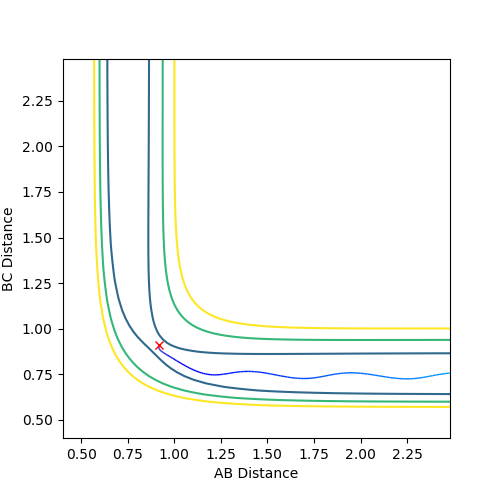 |
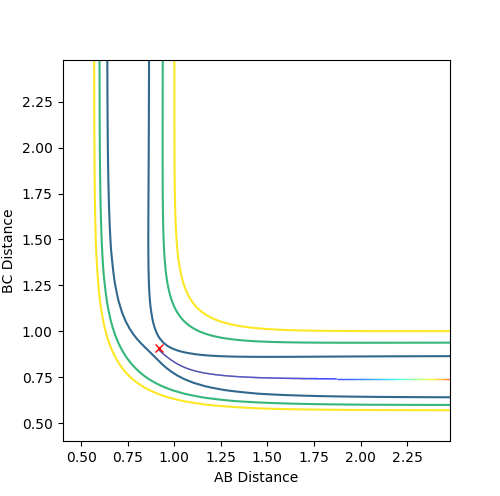
|
| Contour plot A | Contour plot B |
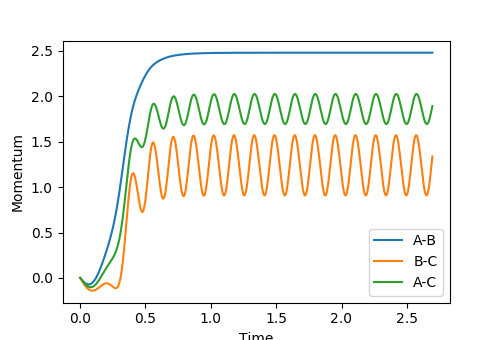
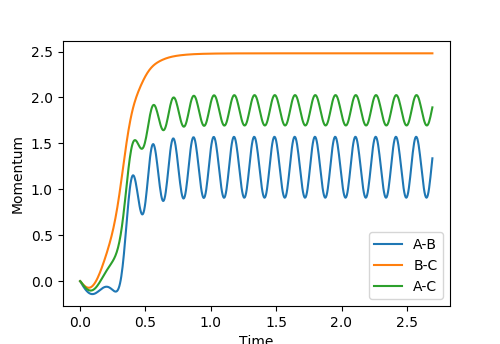
Look at the “Internuclear Distances vs Time” and “Internuclear Momenta vs Time”. Take note of the final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t.
r1(t) = 0.7570 r2(t) = 10.4475 p1(t) = 1.3509 p2(t) = 1.9030
What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead?
The momentum values p2(t) and p1(t) would swap values.
| Original values | r1 = rts and r2 = rts+0.01 |
|---|---|
 |
|
| Momentum graph A | Momentum graph B |
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Total energy | Reactive/Unreactive | Dynamics contour plot | Comment on Trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -98.4330 | Reactive | 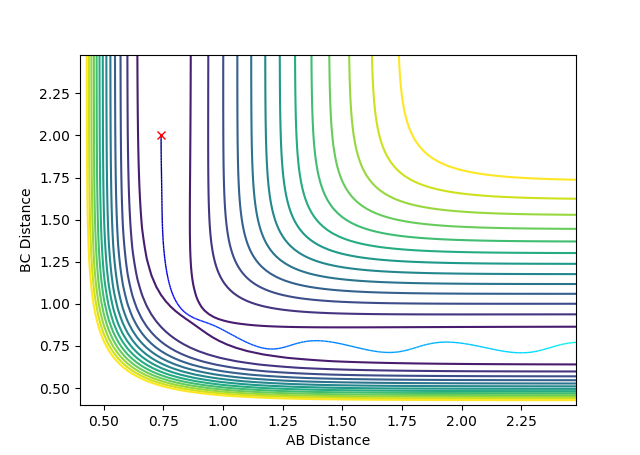 |
B-C bond formation occurs as there is enough energy to overcome the transition state. Hydrogen atom C approaches with enough momentum to produce the product B-C following collision with A-B. |
| -1.5 | -2.0 | -99.8835 | Unreactive | 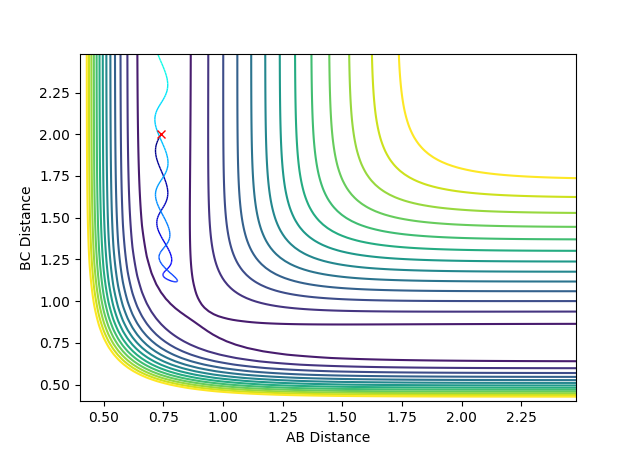 |
There is not enough energy produced from the momentum of atom C to produce the new bond B-C from the reactant A-B. The AB bond vibrates more than the above contour plot but there is not enough momentum to overcome the transition state so the atom C moves away from A-B in the opposite direction. |
| -1.5 | -2.5 | -99.0225 | Reactive | 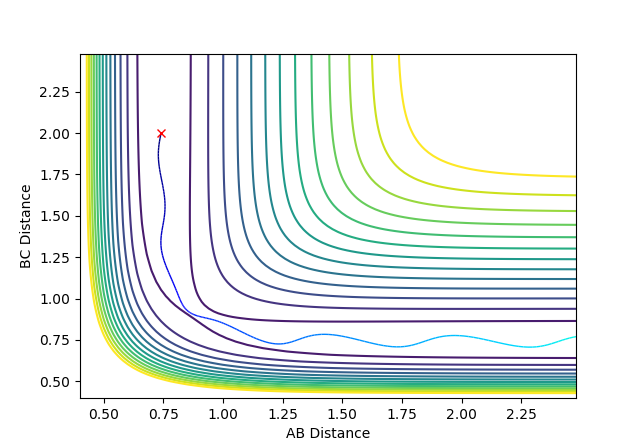 |
B-C bond formation occurs as there is enough momentum from atom C to produce a collision with the energy to overcome the transition state. |
| -2.5 | -5.0 | -84.6913 | Unreactive |  |
The bond formation of B-C does actually occur as there is enough momentum to overcome the transition state. However atom C approaches the A-B with high energy to produce B-C but as a result, the product B-C now has a high energy and re-collides with atom A, overcoming the transition state again to reproduce the reactants. This high energy collision produces a highly oscillating A-B bond and a high energy atom C. This is known as a re-colliding process. (Almost. It's called barrier re-crossing. Fjs113 (talk) 14:12, 28 May 2018 (BST)) |
| -2.5 | -5.2 | -83.8566 | Reactive | 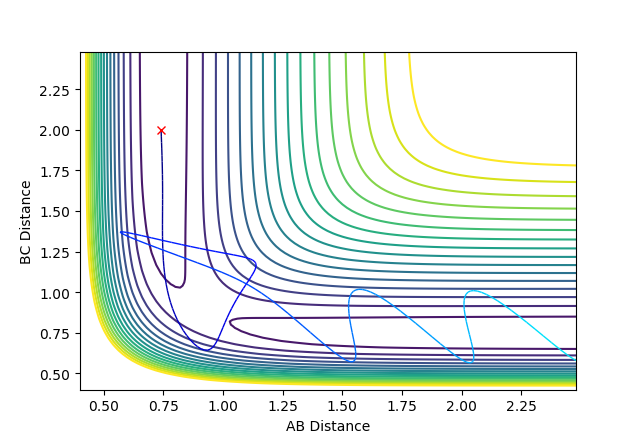 |
Overall, B-C formation is permanent. Hydrogen atom C collides with A-B with very high energy to produce B-C. This formed B-C bond has such a high energy that it breaks and the resultant atom B collides with atom A to reproduce the original reactants. These newly reformed original reactants now collide again, crossing the transition state for the third time to produce the bond B-C. |
'State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?'
Transition state theory (TST) is based on the assumption that atomic nuclei behave according to classic mechanics. It is assumed that reactions will not occur unless atoms or molecules collide with enough energy to form the transition structure. However, according to quantum mechanics, there is a possibility for any barrier with a finite amount of energy that quantum tunneling can occur. This is where particles can tunnel across an energy barrier without actually having the required energy to cross it; as barrier height decreases, tunneling probability increases.
TST assumes recrossing cannot occur but as shown in the calculations, re-crossings is possible. The fourth and fifth set of the above table display recrossing. Recrossing is a passage over the potential energy barrier which separates two species followed by a return to the original side.
TST fails at high temperatures. Theory assumes reaction system will pass over the lowest energy saddle point on the potential energy surface. However, at high temperatures, molecules populate higher energy vibrational modes, which leads to more collisions which can lead to transition states far away from the lowest energy saddle point. Experimental energy values at higher temperatures would be higher than the theoretical values.
(This is good. However, ignoring re-crossing will give higher predicted values, which you haven't mentioned here. Fjs113 (talk) 14:12, 28 May 2018 (BST))
F-H-H
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 --> H-F + H is an exothermic reaction as can be seen in the energy surface plot above. The products are at a lower energy than the reactants which is characteristic of an exothermic reaction. The fluorine atom collides with the hydrogen molecule to produce F-H and a hydrogen atom - the system decreases in energy to become more stable.
H-F + H --> F + H2 is an endothermic reaction as it is the reverse process of the above reaction and forming the reactants again. As seen in the above energy surface plot, the reactants are found at a higher energy than the products which is characteristic for an endothermic reaction.
(Whilst you refer back to the plot, a layperson would not be able to understand this. Which channel represents the reactants and which the products? Labelling the plot would've helped. Fjs113 (talk) 14:12, 28 May 2018 (BST))
'Locate the approximate position of the transition state.'
The F-H bond distance was estimated at 1.8099Å and the H-H bond distance was estimated to be 0.7475Å at the transition state. This was determined by varying inter-nuclear distances in dynamics calculations. As shown in the inter-nuclear distances vs time graph above, the transition state exists for ~ 5 seconds as all the inter-nuclear distances remain the same for this period of time. However, after 5 seconds the transition state begins to collapse as A-B and A-C increases as time increases.
'Report the activation energy for both reactions.'
Hammond's postulate is where a transition state and an unstable intermediate occur consecutively during a reaction process and have nearly the same energy; their inter-conversion only requires a small reorganization of the molecular structures. Hammond's postulate was used to predict structures either side of the transition state to estimate the activation energies of the following reactions:
F + H2 --> H-F + H H-F + H --> F + H2
The initial and final states were found for both reactions and the energy difference was found to find the activation energy. MEP calculations were performed.
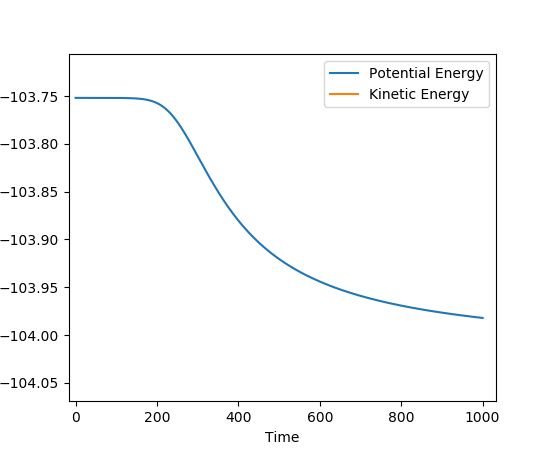
For the F + H2 --> H-F + H reaction, an activation energy of -103.75 - -103.982= 0.23 KCal/mol was obtained (A-B=1.81107, B-C=0.745, pAB=pBC=0 steps=200000).
For the H-F + H --> H2 + F reaction, an activation energy of -103.75 - -133.96= 30.21 KCal/mol was obtained (A-B=1.80, B-C=0.745,pAB=pBC=0, steps=70000).
The F + H2 --> H-F + H reaction is more likely to occur and dominate because it has a much lower activation energy - it is also an exothermic reaction and therefore the products of the reaction are much more stable than the reactants.
Identify a set of initial conditions that results in a reactive trajectory for the F + H2
A-B= 2.3, B-C= 0.74, pAB= -1 pBC=-0.5 The below plots show this trajectory is reactive.
 |

|
| Contour plot | Surface plot |
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
F + H2 --> H-F + H
When this reaction occurs there is a large release of reaction energy and so is an exothermic reaction. The products are much lower in energy compared to the reactants and hence are more stable. However, due to the 1st Law of Thermodynamics, energy cannot be created or destroyed but can be transformed from one form to another. The loss in potential energy is transformed into an increase in kinetic energy. This can be observed in the below inter-nuclear momenta vs time graph. After the transition state collapses at time 2, there is a large increase in the amplitude of the oscillations of the A-B bond (H-F). The H-F bond has a very high vibrational energy and this causes the release of heat.

If radiation is observed from excited product molecules then this is clear indication that the products from the reaction are made in the excited state. Experimentally, infra-red spectroscopy can be used to confirm the mechanism because if the excitation energy is mainly vibrational then IR peaks will be produced. [1]
(This is a good suggestion. Some more details would have been useful, e.g. mentioning vibrational modes etc. Fjs113 (talk) 14:12, 28 May 2018 (BST))
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
| A-B= 0.88, B-C= 2.2, pHF= -0.5 pH=-9 | A-B= 2.3, B-C= 0.74, pHF= -4.9 pH=2 |
|---|---|
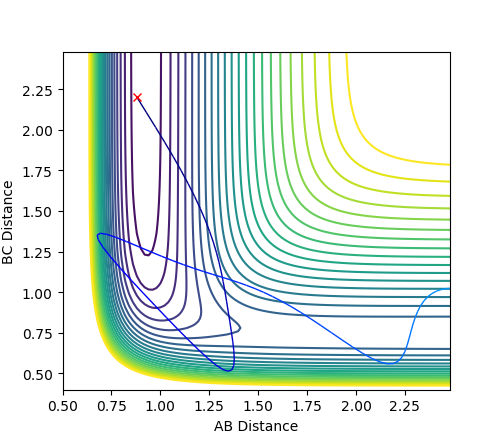 |
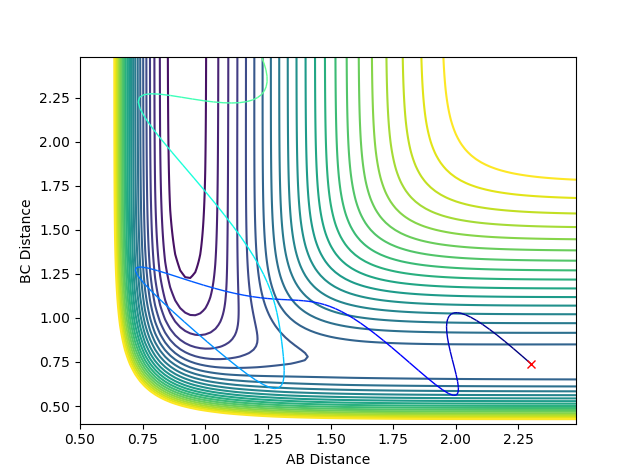
|
| H-F + H --> F + H2 | F + H2 --> H-F + H |
Polanyi's rules state that the vibrational energy is more efficient at promoting a late-barrier reaction than translational.[2] It also states the opposite; translational energy is more efficient at promoting an early-barrier reaction than vibrational energy. A late-barrier reaction is one where the transition state is late and resembles the products whilst an early-barrier reaction is one where the transition state is early and resembles the reactants.
The reaction of F + H2 --> H-F + H is exothermic and therefore resembles the early transition state as per Hammond's postulate. To overcome the activation energy barrier, not much vibrational energy is required. This is shown in the above inter-nuclear momenta vs time graph where only a little momentum is required to set off the reaction.
The reaction of H-F + H --> F + H2 is endothermic and therefore resembles the late transition state, again predicted by Hammond's postulate. To overcome the activation energy barrier, a lot of vibrational energy is required.