MRD:cyy113 MRDLab

EXERCISE 1: H + H₂ system

Definitions

In this exercise, we define the reaction as follows:

Figure 1: A schematic defining the relative positions of hydrogen atoms A, B and C.

1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At both the minimum and the transition structure, it can be observed that the gradients are zero. Mathematically, $\frac{\partial V}{\partial r_{AB}}=0$. The transition structure has the highest potential energy and lies on a maximum point on this curve, while the minima corresponds to the product at equilibrium bond distance. It has the lowest potential energy and lies on the minimum point. They can be mathematically distinguished by taking the second derivative $\frac{{\partial }^{2}V}{\partial r_{AB}^2}$. By definition, $\frac{{\partial }^{2}V}{\partial r_{AB}^2}>0$ and $\frac{{\partial }^{2}V}{\partial r_{AB}^2}<0$ for a minimum and maximum point respectively.

Nf710 (talk) 16:23, 9 June 2017 (BST) This is correct but only in the reaction coordinated which is obtained by taking a linear combination of the r1 and r2.

Initial Run

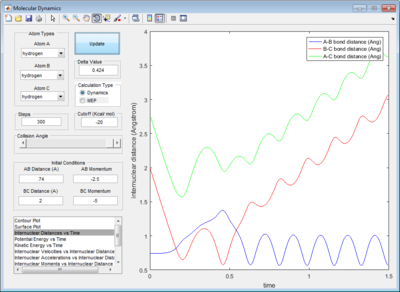
2. Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

To determine the point corresponding to the transition structure, the following properties of the transition structure were considered:

1. The potential of the system is at a maximum point.
2. The transition state lies along the reactive trajectory (black line)
3. Vibrational dampening occurs significantly. We could imagine that initially, symmetric stretching and compression gives rise to variations in r_AB and r_BC. The single atom can also translate towards and away from the H2 molecule. However, at the transition state, symmetric stretching and compressions cancel each other out and a translational degree of freedom is lost for the single atom.

An initial calculation was performed with the following parameters, where p is the momentum: rAB = 0.74Å; rBC = 2.30Å; pAB = 0; pBC = -2.70, dynamic calculation with step size = 300 Using the data cursor, the point where trajectory intersects within the region of the maximum point on the potential energy surface was estimated to be 0.9061Å. (fulfilling conditions 1 and 2). The maximum point region was chosen as the transition state is defined as a structure with the highest potential energy. (Figure 2)

Figure 2: Potential energy surface showing the intersection between the trajectory and the potential energy curve.

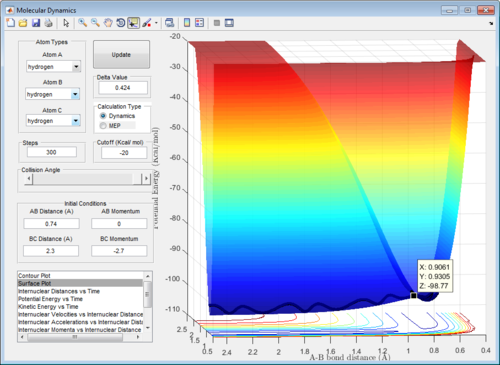
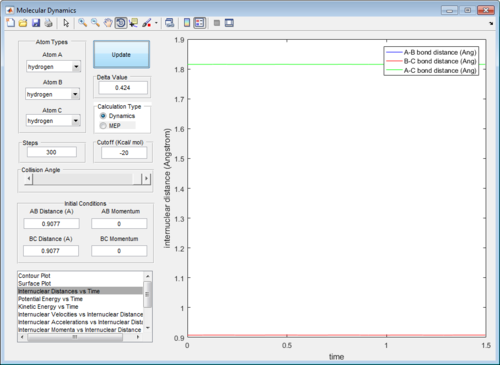
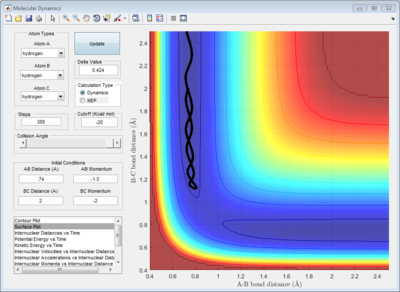
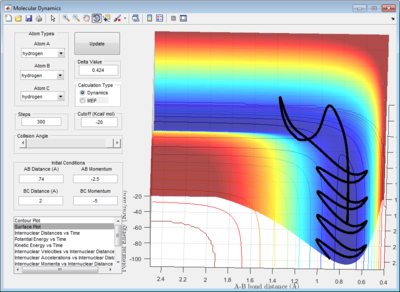
In order to obtain a more accurate value, the r_AB and r_BC were first set to be 0.9061Å. The momentum was set to be 0, since at the transition structure all atoms A, B and C remain stationary. r_AB and r_BC were optimized until the internuclear distances were constant with time in order to fulfill condition 3 of the transition structure. (Figure 3)

Figure 3: Internuclear distance vs time graph calculated by mep.

Only for reactions where all 3 atoms are the same, the intersection point on this curve corresponds to the transition state. rAB = rBC = 0.90775Å and rAC = 1.185Å. It was expected that rAC is twice of rAB or rBC, since atoms A, B and C were in contact with each other in the transition structure and all atoms A, B and C are hydrogen atoms. The blue rAB line could not be observed as it overlapped with the red rBC line. Hence, rts was best optimised to be 0.90775Å. There was minimal vibrations observed as well, which further confirms that a transition state occurs at these values of rAB and rBC.

In addition, the animation showed that the oscillation of AB, BC and AC bond distances with time were so slow that it was not possible to visually observe a change in the position of atoms A, B and C with time.

3. Comment on how the mep and the trajectory you just calculated.

In the mep calculation, r_AB was set at 0.91775Å, which is slightly displaced from the previously determined r_AB distance of 0.90775Å at transition state. Step size was set at 20000. This was done so that the slight perturbation allowed to system to proceed towards either the reactants or products, instead of remaining stationary on the maximum point of the transition state. In the mep calculation, vibrational energies are assumed to flow in and out of the system during the reaction such that it remains zero throughout.

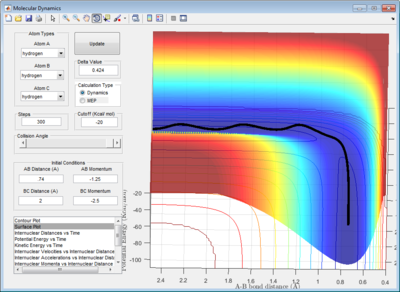
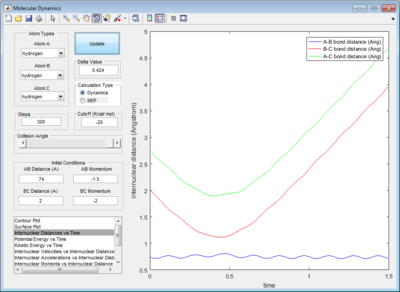
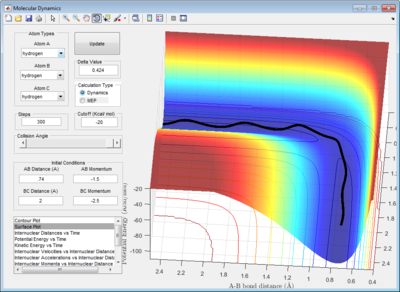
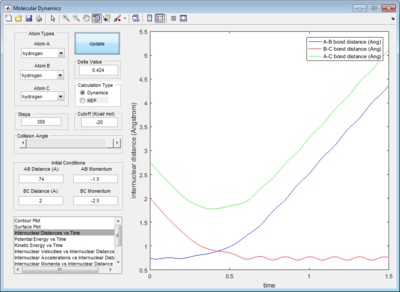
The dynamic calculation shows an oscillating trajectory while the mep calculation shows a non-oscillating one. This was because as the central atom B vibrates, r_AB and r_BC changes in an inverse relationship. (i.e. if r_AB increases then r_BC decreases, and vice-versa).

In addition, the range of the trajectory was similar with a step size of 5000 in dynamic calculation and 20000 in mep calculation. (Figure 4) This suggests that in the mep calculation, each step size corresponds to a smaller fraction of the molecule's trajectory.  

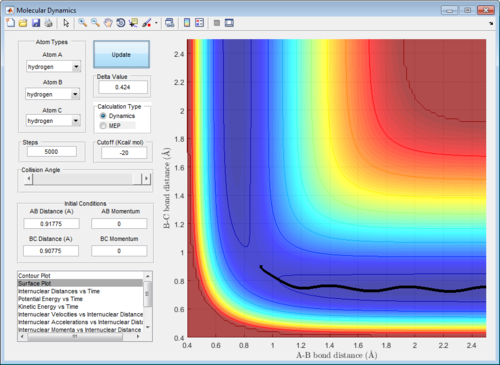
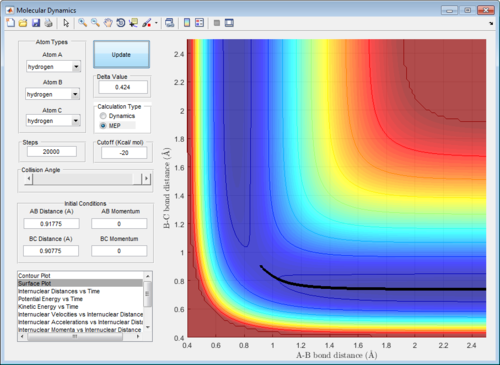
Figure 4: Potential energy surfaces showing the trajectories in a (left) dynamic calculation with step size = 5000 and (right) mep calculation with step size = 20000

Figure 5: Potential energy vs. time curve showing the change in potential energy from transition state to products.

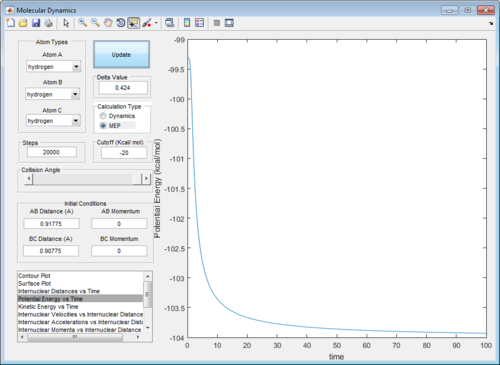
The presence of vibrational energies in a dynamic calculation makes it hard to determine accurately the activation energy. Running an mep calculation removes these vibrational energies and greatly simplifies the determination of activation energy. Plotting the potential energy vs time, the activation energy for this reaction is determined to be 4.7 kcal/mol. (Figure 5) 

Nevertheless, it would not be possible to run an mep calculation without first running a dynamic calculation. In order to obtain a full trajectory, an impossibly large number of step size would be needed and the calculation will take too long. Hence the dynamic calculation not only provides a more accurate picture of the trajectory taking into account vibrational energies, it also allows us to screen for the transition state region so we can 'zoom' into it in the subsequent mep calculation.

Further Runs with Modified Variables

Figure 6: Potential energy vs time curve showing the change in potential energy from the transition state in the direction opposite from that of Figure 5

What would change if we used the initial conditions r₁ = r_ts and  r₂ = r_ts+0.01 instead?

A further mep calculation was performed, but switching only the variables r_AB and r_BC. (i.e. r_AB = 0.90775Å, r_BC = 0.91775Å) This simulated the perturbation of the system from the transition state in the direction opposite from the initial run, in order to study the other half of the reaction profile. It was observed that the shape of the potential energy curve did not change, nor did the activation energy. This was expected since all the atoms were hydrogen and consequently the reaction profile diagram is symmetrical about the transition state. (Figure 6)

Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?

This can be envisioned as the backward reaction. In this case, the enthalpy of reaction is still zero and the activation energy remains the same since there the reactants were the same as products.

Reactive or non-reactive trajectories

For the initial positions r₁ = 0.74 and r₂ = 2.0, run trajectories with the following momenta combination. (step size was fixed at 300).

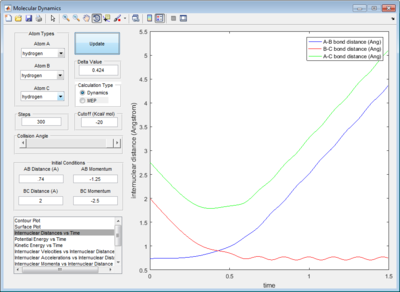
4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

p1	p2	Trajectory	Internuclear distance with time	Comments
-1.25	-2.5			Reaction is possible. Trajectory passes through the saddle point (transition state) to reach the products. There is one collision in the reaction and it is clearly marked as an intersection point on a plot of internuclear distance with time.
-1.5	-2.0			Reaction is not possible. Trajectory does not pass through the saddle point (transition state) to reach the products. There were no collisions as clearly observed by the lack of any intersecting points on a plot of internuclear distance with time. Compared to scenario 3, p2 is not sufficiently large enough for a reactive collision to occur.
-1.5	-2.5			Reaction is possible. Trajectory passes through the saddle point (transition state) to reach the products. There is one collision in the reaction and it is clearly marked as an intersection point on a plot of internuclear distance with time.
-2.5	-5.0			Reaction is not possible. While the trajectory does pass through the saddle point (transition state), it does not reach the products.There are 2 collisions in the reaction as clearly marked by the 2 intersection points on a plot of internuclear distance with time. After the first collision, too much excess energy is transferred to the displaced H atom such that it reverses its trajectory and collides with the newly formed H2 molecule.
-2.5	-5.2			Reaction is possible. Trajectory passes through the saddle point (transition state) thrice but eventually reaches the products. There are three points of the reaction where the molecules collide and they are clearly marked on a plot of internuclear distance with time. While there was significantly excess energy transferred to the displaced H atom and the trajectory is reversed, the trajectory still ends up towards the products after a series of collisions.

5. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The Transition State Theory (TST) assumes the following:

1. Once a system has past the transition state to form products, it cannot reverse to reform reactants.
2. At the transition state, translation motion can be treated classically and is independent of other forms of motion.
3. All transition states becoming products can be fit into a Maxwell-Boltzmann distribution whether or not an equilibrium actually exists between the reactants and products.

Using this theory, it is possible to calculate the rate constant k as follows:

$k=k_{B}T{K}^{\ne }/h$ , where $k$ is the rate constant, $k_B$ is the boltzmann constant, $T$ is temperature in Kelvins, $K^{\ne }$ is the equilibrium constant between the reactants and transition state and $h$ is Planck's constant. Hence, $k$ can be calculated with only the fundamental properties of the species involved, without regard for their interaction with each other. However, it has several limitations.

Scenario 4 clearly demonstrates that recrossing of the transition state can occur even through the system has past the transition state. This could have occurred due to a variety of reasons, such as quantum mechanical tunnelling through the transition state energy barrier or because the true transition state occurred away from the saddle point. In fact, it has been reported that the latter reason is significant in the H + H₂ reaction. The excess energy from the collision causes the reaction products to occupy a higher vibrational mode resulting in a different transition state not predicted by the TST.

Even in scenario 5 where the reaction is possible, TST cannot provide an account for the multiple recrossing of transition states. There is a different value of K associated with each barrier recrossing and they cannot be determined by TST which assumes only one value of K for the entire reaction.

EXERCISE 2: F + H₂ system

Definitions

In this exercise, we define the reaction as follows:

Figure 7: A schematic defining the relative positions of Fluorine atom A and Hydrogen atoms B and C.

6.Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The F + H₂ reaction is exothermic while the H + HF reaction (backward reaction) is endothermic, as can be observed in the potential surfaces obtained by a dynamic calculatoin at step size = 3000. (Figure 8) This is expected, as the H-F bond (-567 kJ mol^-1) includes ionic contributions not found in H-H bonds (-432 kJ mol^-1) as a result of the electronegativity of the F atom and will hence be stronger.

Figure 8: Potential energy surface showing the variation of potential energy with r_AB

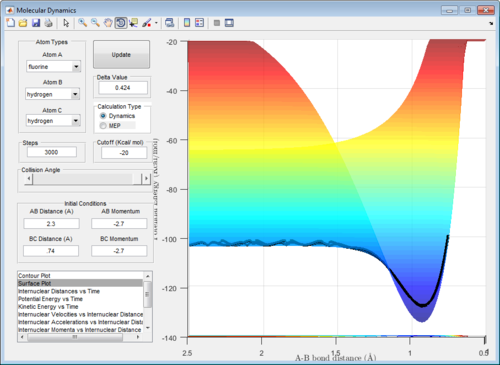
Running the calculation

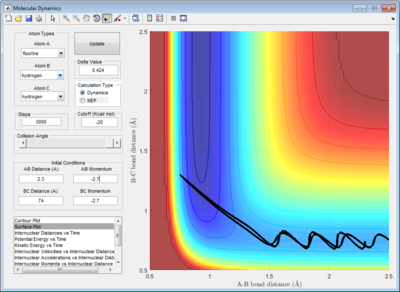
7. Locate the approximate position of the transition state.

Figure 9: Potential energy surface obtained by increasing step size to 5000. The small difference between reactant and transition state energies still could not be resolved.

Since the F atom is highly reactive, its energy is extremely close to the transition state energy, hence it was difficult to determine a rough estimate of r_AB and r_BC at which the transition state occurred visually, even after increasing the step size to 5000 (Figure 9). Using the data cursor, it was observed that the energy remained around -103.7 kcal/mol before decreasing further. It was likely that the energy levels were so close that the potential energy surface was not able to resolve the minor differences. Hence, to obtain a rough estimate of r_AB and r_BC in the transition state, the maximum value of r_AB and r_BC was chosen such that the energy still remained at -103.7 kcal/mol but anymore deviations would have caused the energy to decrease further. The set of values were determined to be r_AB=1.82Å and r_BC=0.74Å.

Figure 10: Plot of internuclear distance with time using r_AB and r_BC at the transition state region.

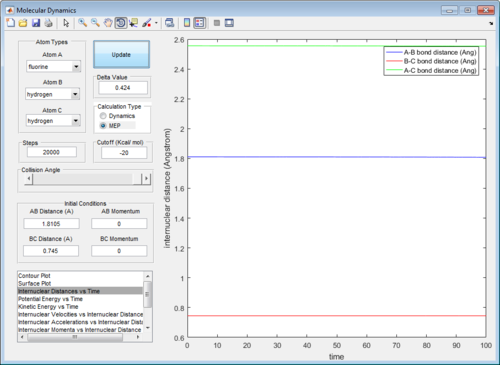
Next, this set of values were optimised by plotting the internuclear distance vs time in an mep calculation. At the transition state, the internuclear distance does not vary with time and a straight horizontal line will be observed. The values were optimised within this region and found to be r_AB=1.8105Å and r_BC = 0.745Å. (Figure 10) This agreed with the Hammond's Postulate, which states that for an exothermic reaction, the transition state resembles the products. it can be observed that r_BC=0.745Å was extremely close to the initial r_BC set at 0.74Å














8. Report the activation energy for both reactions.

Using this optimised set of parameters of r_AB and r_BC ,the potential energy vs time curve was plotted in a mep calculation. Removal of vibrational energy near the transition state allows the activation energy to be determined simply without the complication of energy fluctuations due to vibrations. The activation energies were determined to be 0.21 and 30.1 kcal/mol respectively for the forward and backward reaction. In the forward reaction, it is noted that the step size used in the forward reaction calculation was much higher and r_AB was slightly increased to 1.8305Å because we wanted to introduce a perturbation to tip the transition state back towards the reactants. (Figure 11)

Figure 11: Potential energy with time curves for (left) forward reaction

(right) backward reaction

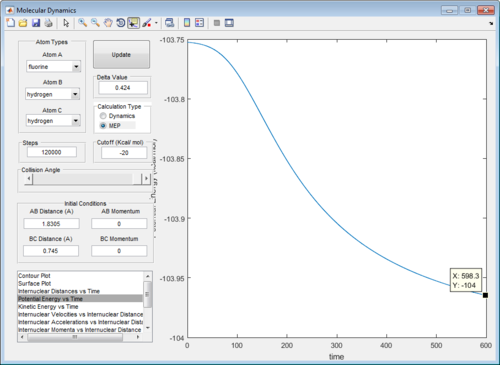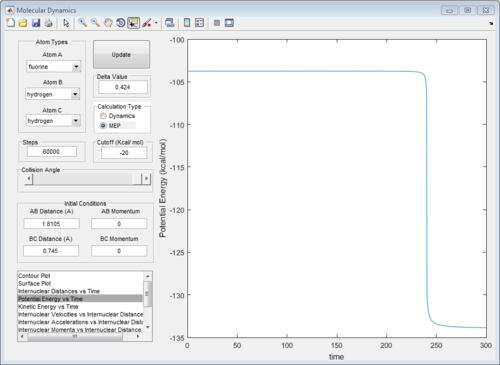Nf710 (talk) 16:36, 9 June 2017 (BST) A dynamics calculation would have been better here.

Analysis

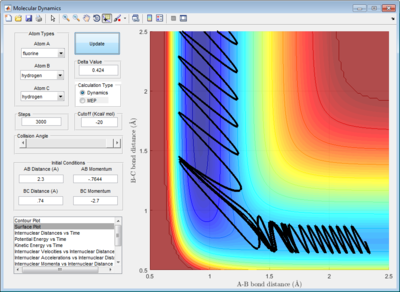
9. Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Figure 12: Potential energy surface showing the reactive trajectory when r_BC= 0.745Å, r_AB = 1.55Å, p_AB = -0.4, p_BC = -1.2.

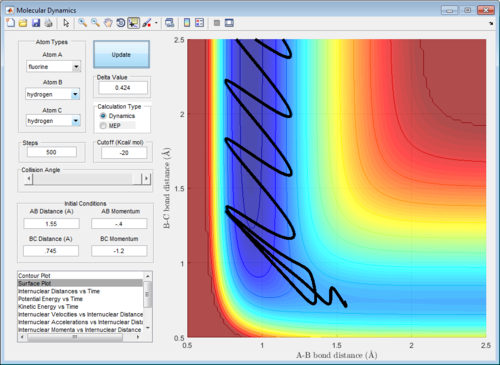
Nf710 (talk) 16:38, 9 June 2017 (BST) This is not a reactive trajectory you are start from the wrong side of the TS!

In comparison to the initial H + H₂ reaction, F is more reactive than the H atom. As such, r_AB and p_AB were reduced in comparison to r_BC and p_BC in order to prevent barrier recrossing past the transition state. Indeed, it can be observed that the reaction occurs with the following set of parameters: r_BC= 0.745Å, r_AB = 1.55Å, p_AB = -0.4, p_BC = -1.2. (Figure 12)

Because energy must be conserved, the excess reaction energy for an exothermic reaction will be released into exciting the products into higher translational, vibrational, rotational and electronic energy levels. The populations of the products in these levels can be calculated via the partition functions as follows:

$q^T=V/{\mathrm{\Lambda }}^3,\mathrm{\Lambda }=h/\sqrt{(}2\pi mkT)$
$q^V=1/(1-exp(-\beta \epsilon ))$
$q^R=\sum _J(2J+1)exp[-\beta hcB\tilde{J}(J+1)]$
$q^E=g^E$

Translation is the only mode that gives rise to kinetic energy. As such, the average change in translational energy can be simply measured as the change in temperature of the system. Vibrational and rotational energy levels result in the internal energy of the species and any changes can be measured via rovibrational spectroscopy in the IR region. Electronic energy levels can be measured in an emission spectrum within the UV/vis region. While there are reactions which gave rise to an electronically excited product (i.e. chemiluminescent reactions), in this H+H₂ or F+H₂ reaction it is unlikely to occur, since the energy gaps between the low-lying orbitals (1s to 2s and 2p to 3s for H and F respectively) is too great.

Nf710 (talk) 16:43, 9 June 2017 (BST) This is correct on the whole and is a very good answer however this model is only able to probe the vibrational and trandlational. But excellent use of the partion functions to explain the energy levels.

10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

The effect of translational and vibrational energy on a reaction can be explored through Polanyi's empirical rules which apply when an atom attacks a diatomic species. In this set of rules, if a reaction has a late transition state, it will be promoted by a high vibrational energy and a low translational energy, and the reverse is true. Understood in terms of Hammond's Postulate, an exothermic reaction (hence a late transition state resembling the products) is more likely to proceed if it has a high vibrational and low translational energy. The reactions F + H₂ and H + HF studied in this example can be used to confirm if Polanyi's empirical rules in the table below:

Reaction	rAB /Å	rBC/Å	pAB	pBC	Trajectory	Comments
F + H2	2.30	0.74	-2.7	-2.7		No reactive trajectory
F + H2	2.30	0.74	-0.7644	-2.7		Reactive trajectory observed
H + HF	0.74	2.30	-2.7	-2.7		No reactive trajectory
H + HF	0.74	2.30	-2.7	-0.4		Reactive trajectory observed

Well done for proving polyanis rules however fig 2 is reactive with vibrational energy and an early TS so you are contradicting what you are saying. either way this is a very good report. well done.