MRD:cd1017

H + H₂ System

The transition state is defined as the maximum on the minimum energy path linking reactants and the products, and therefore, on a potential energy surface diagram, a transition state is where:

$\frac{\partial V(r)}{\partial r}=0$ and $\frac{{\partial }^{2}V(r)}{{\partial }^{2}r}<0$

The mathematical definition of a local minimum is similar:

$\frac{\partial V(r)}{\partial r}=0$ and $\frac{{\partial }^{2}V(r)}{{\partial }^{2}r}>0$

Excellent, what about mentioning the saddle point, how would you describe this? With your mathematical derivatives I would go back and correct the notation for f"(x). Mys18 (talk) 13:20, 19 May 2019 (BST)

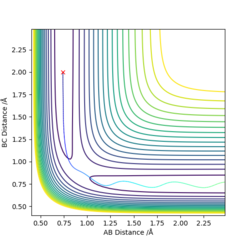
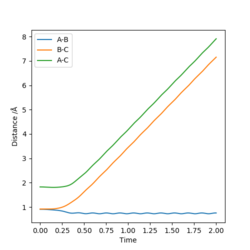
When the three-atom system is at the transition state, the best estimation for the intermolecular distances is r₁ = r₁ = 0.908, for both A-B and B-C distances are constant and the momentum of the system is 0.

Internuclear Distances vs Time

Do you mean r1 and r2... Good, the internuclear distances do not change, what are the units for you value? Nicely laid out, but perhaps link your explanation to your graph to describe how you know this information. Mys18 (talk) 13:46, 19 May 2019 (BST)

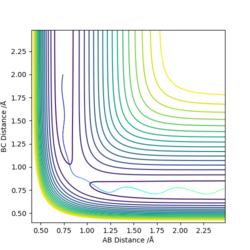
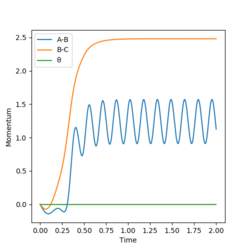
The condition is changed to: r₁ = 0.918, r₂ = 0.908, p₁ = p₂ = 0. Both plots clearly show the trajectory: after the collision, the A-B distance increases and B-C distance decreases, showing that H_B and H_C form a new dihydrogen molecule. The dyamics plot shows the vibration of the atoms, while the MEP plot doesn't. Hence, the MEP plot is a less realistic representation than the dynamics plot. However, the trajectory of the MEP plot goes through the bottom of the potential surface, and therefore, has a lower potential than the dynamics at a certain point (r₁, r₂).

The MEP contour plot of the trajectory.

The Dynamics contour plot of the trajectory.

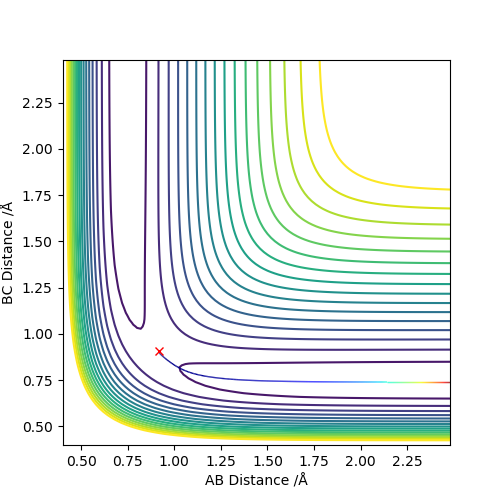
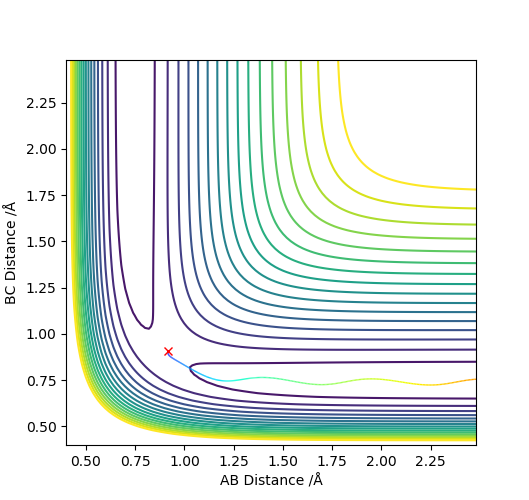
Correct we see the vibration motion for the dynamics method via oscillations. For MEP method the KE is set to zero, so what other energies are not conserved besides the vibrational motion? Mys18 (talk) 14:52, 19 May 2019 (BST)

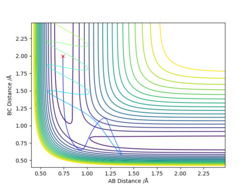
If the values of r₁ and r₂ are exchanged, the corresonding atom distances and momenta will be exchanged as well.

r1 = 0.918 r2 = 0.908		r1 = 0.908 r2 = 0.918
Internuclear Distacne vs. Time	Momenta vs. Time	Internuclear Distacne vs. Time	Momenta vs. Time

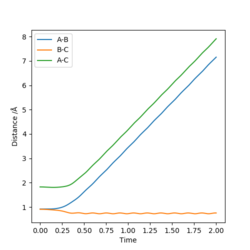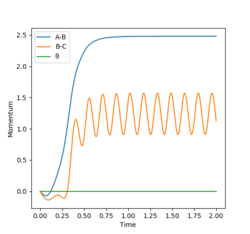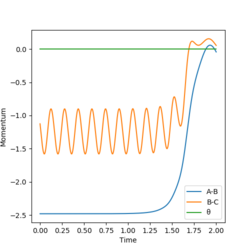
The final conditions (t = 2.00)of the first calculation (r₁ = 0.918, r₂ = 0.908) are: r₁ = 7.155, r₂ = 0.756, p₁ = 2.481, p₂ = 1.126, and another calculation is done with the initial condition r₁ = 7.155, r₂ = 0.756, p₁ = -2.481, p₂ = -1.126. It can be seen that it is a reversed process of the first calculation, and its final conditions are the initial conditions of the first calculation.

Internuclear Distacne vs. Time	Momenta vs. Time

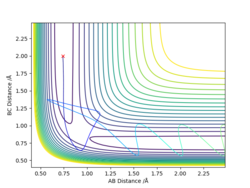
For the initial positions r₁ = 0.74, r₂ = 2.0:

p1	p2	Etot	Reactive?	Plot	Description of the Dynamics
-1.25	-2.50	-99.0	Y		The Molecule HAHB approaches HC without vibration;however, as the distance decreases, they collide and the reaction happens, and the new dihydrogen molecule starts to vibrate.
-1.50	-2.00	-100.5	N		The Molecule HAHB approaches HC with vibration, and they collide and bounce back. No reaction happens and the dihydrogen molecule keeps vibrating.
-1.50	-2.50	-98.9	Y		The Molecule HAHB approaches HC with vibration;however, as the distance decreases, they collide and the reaction happens, and the new dihydrogen molecule keeps vibrating.
-2.50	-5.00	-84.9	Y		The Molecule HAHB approaches HC without vibration;however, as the distance decreases, they collide and the reaction happens, and the new dihydrogen molecule starts to vibrate. The amplitude of the vibration is significant, and therefore, the new dihydrogen molecule and HA collide and react again, and the resulting dihydrgen molecule kepps vibrating.
-2.50	-5.20	-83.4	Y		The Molecule HAHB approaches HC without vibration;however, as the distance decreases, they collide twice and the reaction happens, and the new dihydrogen molecule starts to vibrate.

According to the table, after the collision(s), the hydrogen molecule keeps or starts vibrating, and the total energy must be at least -99.0 to trigger the reaction.

In you explanations it might be worth mentioning whether the atoms/molecules have sufficient energy to over come the energy barrier and so pass the TS or not. The reactivities are correct except for ROW 4, this does not occur. The plot suggests the TS is overcome, which quite rightly could be happening, but at a closer look can you spot what happens? It might help to compare this to ROW 5. ideally reactants go to products, but can there be a situation where we get reactants to products to reactants? What can you now conclude? Mys18 (talk) 14:58, 19 May 2019 (BST)

The main assumption for transition state theory is that an activated complex is in equilibrium with the reactants and the rate for it to form the product depends on its rate to pass through the transition state. However, in the absence of information to the contrary, the transmission coefficient is assumed to be about 1, which means most of the activated complex can pass through the transition state. This situation differs from reality, and thus the theoretical value for the reaction rate is higher than the experimental value.

True, what other assumptions do you think exist. One assumption links to the feedback given above. Might be worth reading up on TS theory, (Transition state theory: T. Bligaard, J.K. Nørskov, Chemical Bonding at Surfaces and Interfaces, 2008) and Born Oppenheimer's approximation (Born-Oppenheimer approximation: Iain R. McNab, Encyclopedia of Spectroscopy and Spectrometry, 1999). Mys18 (talk) 15:06, 19 May 2019 (BST)

F-H-H System

PES Inspection

When F atom and two H atoms are close (F-H_A = H_A-H_B = 0.9), a F-H molecule forms and the other H atom leaves. Thus, the formation of HF is thermodynamically preferred since the H-F bond dissociation energy is greater than that of H-H bond, and the reaction F + H₂ → HF + H is exothermic.

The dynamics potential energy surface plot of a F-H-H system.

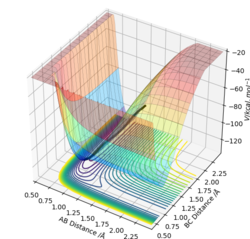
The approximate position for the transition state is found: F-H_A = 1.811 Å, H_A-H_B = 0.745 Å

The activation energy for this reaction is 0.261 kCal·mol^-1

For the endothermic reaction H + HF → H₂ + F, the transition state is: H-H = 0.745 Å, F-H = 1.811 Å

This reaction can happen when the H-H momentum is -5.00, and the activation energy is 16.472 kCal·mol^-1

Excellent and bonus - correct units for all your values. Mys18 (talk) 15:10, 19 May 2019 (BST)

Reaction Dynamics

F + H₂

For the first reaction is reactive, when the initial conditions are: F-H_A = 1.600, H_A-H_B = 0.645, p(F-H_A) = -1.0, p(H_A-H_B) = 5.0. The reaction is triggered by a collision, where the F atom approaches the H₂ molecule, and the F atom attracts a H atom while another H atom leaves in the opposite direction. Because of the conservation of energy, the energy released by the reaction is converted to the kinetic energy of the new particles and the vibrational energy of the new molecule. The vibration can be experimentally detected and measured by IR.

That's a great suggestion! Can we also use the change in heat from this reaction as a measurement? Mys18 (talk) 15:14, 19 May 2019 (BST)

A series of calculations are done (p_FH = -0.5), and it's found that for the reaction to happen, the total momentum for this system must be negative, even though for p_HH, the initial kinetic energy (0.132) is below the activation energy (0.261). Then a calculation is done for the reaction with the same initial positions but with p_FH = -0.8, p_HH = 0.1, the reaction happens after several collisions.

rFH = 1.811, rHH = 0.74
pFH	pHH	Reaction?	KE	Etot
-0.5	-3.0	Y	7.632	-96.111
	-2.0	Y	3.132	-100.611
	-1.0	Y	0.632	-103.111
	0.0	Y	0.132	-103.611
	1.0	N	1.632	-102.111
	2.0	N	5.132	-98.611
	3.0	N	10.632	-93.111

H + HF

A trajectory for this reaction is generated, with the initial conditions: r_HF = 0.93 r_HH = 1.22, p_HF = 14.0, p_HH = 5.0. This reaction has an early barrier, and therefore, according the Polanyi's rules, kinetic energy is effective for the reaction while vibrational energy is not.

Good translation energy is more effective for an early barrier. Is the same true for the endothermic reaction? Although it is easy for someone to infer this information, it is always worth writing out the extra bit. Overall, great report and everything was concisely answered. Perhaps check out the references I've listed above so that you are aware of a few more assumptions, one assumption will aid you greatly on previous questions. Good job :) Mys18 (talk) 15:22, 19 May 2019 (BST)