MRD:cc5115
H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface
The total gradient of the potential energy surface is zero at a minimum and at a transition structure. If a trajectory starts exactly at the transition state with no initial momentum, then it will remain there forever. However, changing the geometry by a small amount in either the direction of the reactant of products, it will start to roll towards either one. To determine a transition state, start the trajectory near the transition state and see whether they start moving or "rolling" towards the reactant or product. For a minima, it is the place where it rolls to and ends at, which is either the reactant or the product.
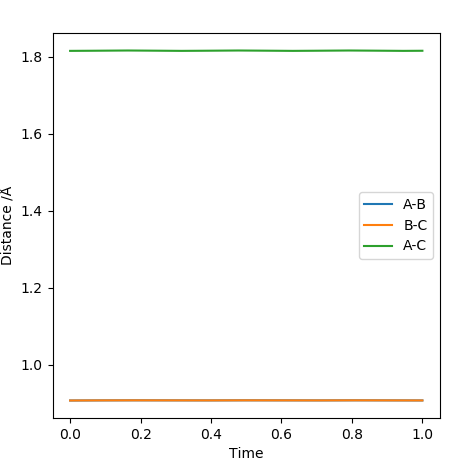
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory
As explained above, if a trajectory starts exactly at the transition state with no inital momentum, the it will remain there forever. Therefore, to estimate the transition state, the graph of "internuclear distances vs time" should look as close as a straight line as possible, as illustrated in the screenshot. This means that when the 3 hydrogen is placed at a particular distance where r1=r2 and no initial momentum, then there should be no particular movement or oscillation. The transition state position is estimated to be rts=0.9077A.
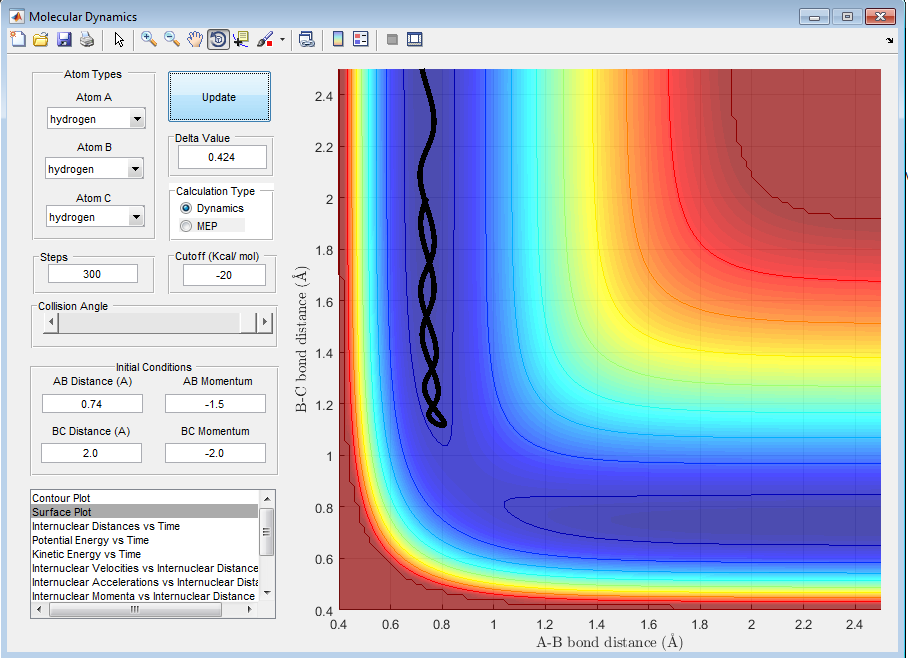
Comment on how the mep and the trajectory you just calculated differ
For the mep, the terminal H at r1 (=rts + 0.01) will slowly move away from the other H atoms and the reaction path will slowly roll towards the products as indicated by the thick black line; the line is a smooth curve when using the mep calculation type. However, the trajectory changes back to being a wavy line when using the dynamics calculation type indicating how the diatomic molecule is vibrating.
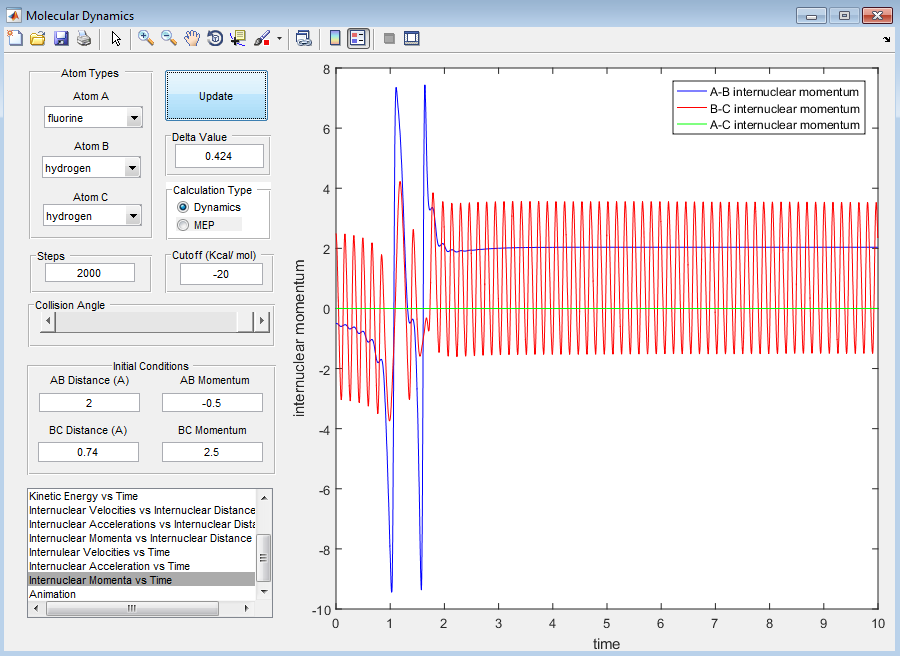
Look at the “Internuclear Distances vs Time” and “Internuclear Momenta vs Time”. Take note of the final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t. What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead?
t=9.995, 2000 steps r1(t) = 36.92, r2(t) = 0.7341 p1(t) = 2.481, p2(t) = 1.546
For final positions (r1(t) and r2(t)) and average momenta (p1(t) and p2(t)), they will swap with each other when the initial conditions are reversed. This is because now the reaction path is slowly rolling towards the reactants instead of the products however the shape of the reaction path still remains the same.
=== Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe? ===
The graphs have the same curves but reversed, meaning at t=9.995, they come back to the initial positions.
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The main assumptions of transition state theory is that the reactants are at the correct orientation which results in a successful collision to form products. This assumes that there is sufficient energy in the collision in order to overcome the kinetic barrier. Therefore, with the results obtained, the transition state theory predictions for the reaction rates will be faster than the experimental values (rate is higher) because one cannot achieve 100% successful collision rate.
F-H-H System
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state. Report the activation energy for both reactions
F + H2 is an exothermic reaction while H + HF is an endothermic reaction. The H-F bond is a very strong bond compared to H-H bond due to the large difference in electronegativity therefore more heat will be released when H-F bond is formed than the heat absorbed to break the H-H bond.
The transition state positions are approximately: AB (HF) is 1.815Å and BC (HH) is 0.745Å.
The activation energy for F + H2 is around 30.6 kcal/mol The activation energy for H + HF is around 0.6 kcal/mol
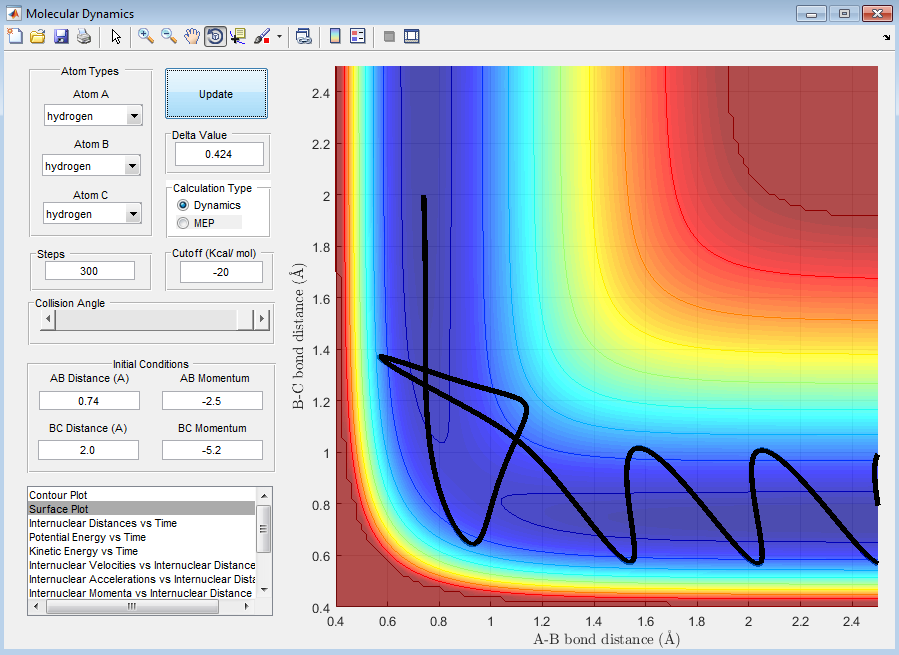
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A set of initial conditions that results in a reactive trajectory for the F + H2 is: AB (HF) = 2.3Å, BC (HH) = 0.74Å, p(AB) = -2.2, p(BC) = 2.8. For this reaction, the energy released is transferred to vibrational energy across the H-F bond as seen by the wavy black line of the reaction path.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state
Polanyi's empirical rules tells that vibrational energy is not as effective as translational energy when it comes to increasing the efficiency of a reaction with an early transition state, and the opposite is true with a late transition state.
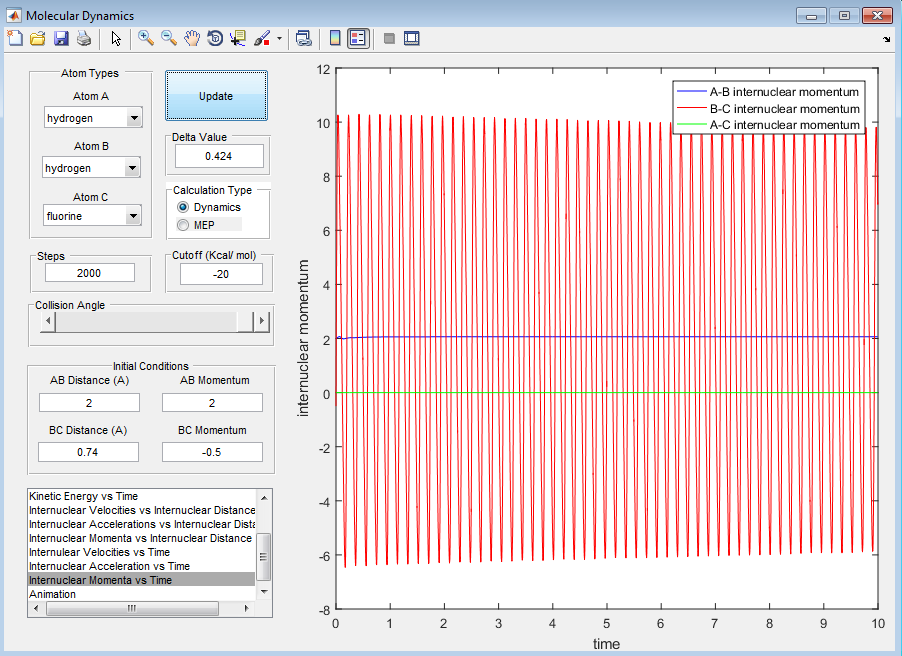
For F + H2:
When the initial conditions are set to have a large vibrational energy of 2.5 and small translational energy of -0.5, from the screenshots provided below the reaction does not occur. However, when we decrease the vibrational energy to 1 and increase the translational energy to -1, the reaction does proceed. This shows how the reaction has an early transition state.
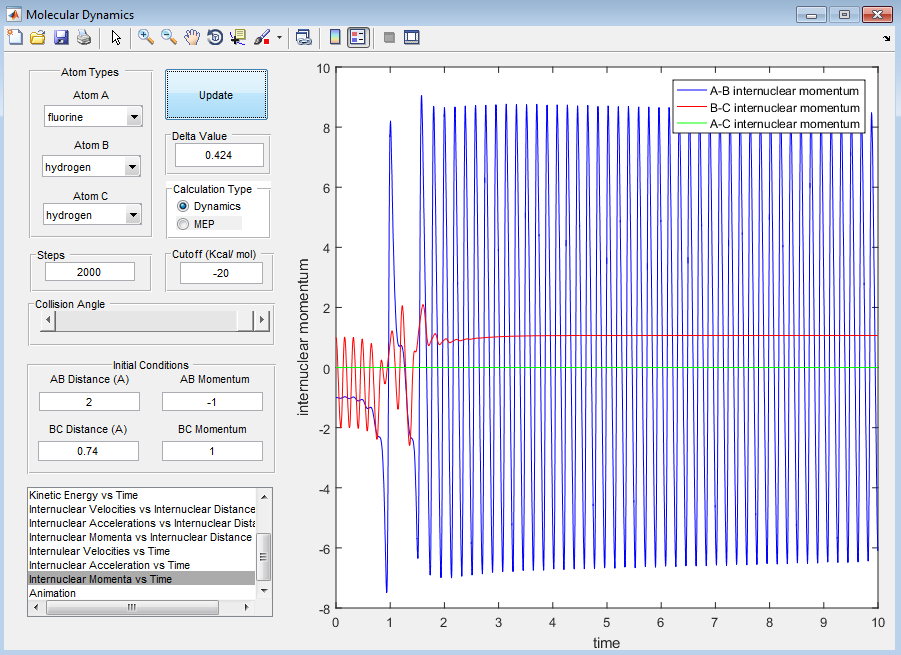
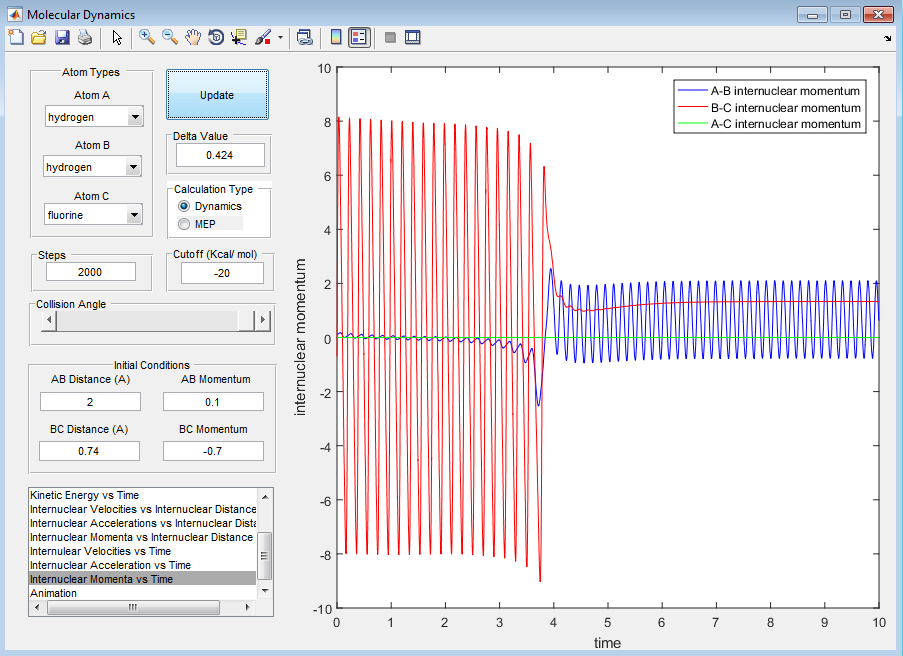
For H + HF:
When the initial conditions are set to have a large translational energy of 2 and small vibrational energy of -0.5, from the screenshots provided below the reaction does not occur. However, when we decrease the translational energy to 0.1 and increase the translational energy to -0.7, the reaction proceeds. This shows how the reaction has a late transition state.