MRD:by1517
F- H distance
H + H2 system
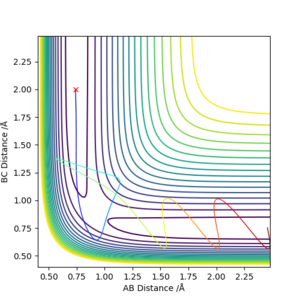
On a potential energy surface diagram, the transition state is mathematically defined as the saddle point. One of the 3 types of stationary points which occurs when fx= 0 and fy= 0 simultaneously for f(x,y). To check, calculate D = fxxfyy - (fxy)2 and substitute (x,y) where it is the parameters for the stationary point. If D < 0, then it is a saddle point.
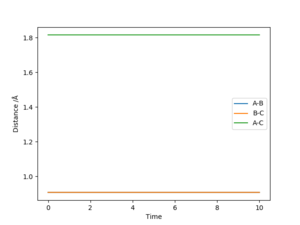
The best estimate for the transition state position (rts) is 0.9077421001 Å, this was found by minizing the forces acting the 3 H atoms. It follows that at the transition state, there would be oscillations. So on an internuclear distance vs time graph, the distances would appear as a straight horizontal line rather than a sinusoidal function. Good description on defining the transition state but how do you distinguish between the local minimum and maximum at the saddle point? Also, how did you minimize the forces acting on H-H-H? Need to explain how you got the this value for the transition position. Sf3014 (talk) 09:53, 22 May 2019 (BST)
Reaction path
If the system is slightly displaced from the transition state, i.e.:
| r1 (HA - HB) | r2 (HB - HC) | p1 | p2 |
|---|---|---|---|
| 0.9087421001 | 0.9077421001 | 0 | 0 |
The system simply falls to the lowest energy state it is closest to.
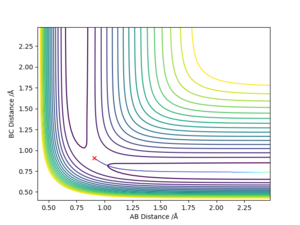
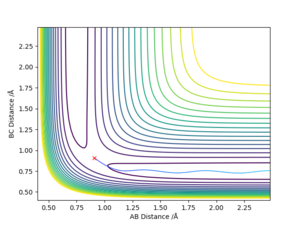
For MEP calculations, the trajectory simply falls to the very bottom of the potential without any vibrations, representing the ground state. In contrast the dynamic calculations trajectories ends up with vibrations at the bottom of the potential.
If instead the displacement was reversed, the trajectory would simply be mirrored along y = x.
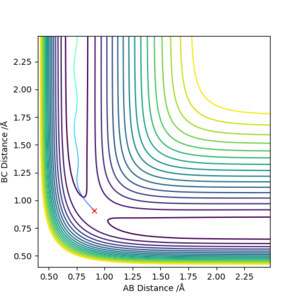
Good observation, but what does this mean? Why is there no vibrations with the MEP calculation?. Sf3014 (talk) 09:57, 22 May 2019 (BST)
Reactive and unreactive trajectories:
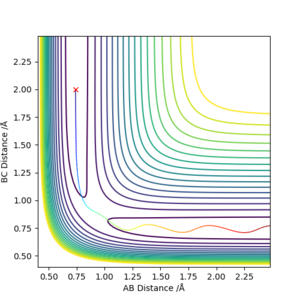
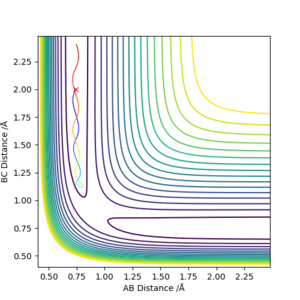
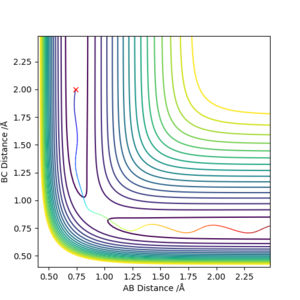
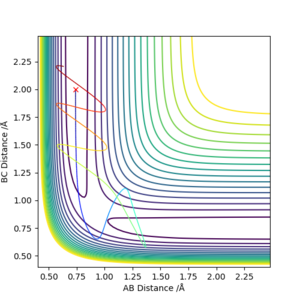
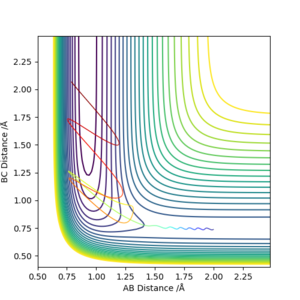
Initial positions : r1 = 0.74 and r2 = 2.0
Having enough energy to cross the activation energy barrier does not always gurantee a successful reaction. The systems can ultimately cross the activation energy barrier serveral times and the reaction is only successful when the conditions of the trajectory (p1, p2, r1, r2) is right.
The transition state theory assumes that the energy of atoms in the reactants follows the boltzmann distribution. This is achieved if the system is given enough time to reach thermal equilibrium. The other assumption is that once the system reaches the transition state with a 'velocity' to the product configuration, it will not return to the transition state again. In other words, it will not return to the reactants state. Additionally, quantum-tunneling effects are ignored and Born-Oppenheimer approximation is used. With the transition state theory, the reaction rate values would be higher compared to experimental values as there will be more successful reactions since once the system reaches the transition state, the product is formed and will not revert back to the reactants. Good observation, but next time included description on the trajectories that you have provided in your table. Also, reference where you got your TST info. Sf3014 (talk) 12:58, 22 May 2019 (BST)
F - H - H system
PES inspection
The potential well along AB distance (F - H) is higher in energy compared to along BC distance(H - H). So there is a decrease in energy of the system when the AB (F - H) distance decreases, hence the reaction of F + H2 → H + HF is exothermic. Logically, the reaction of H + HF → F + H2 is endothermic. Hence it can be said that the F - H bond is lower in energy than H - H, in otherwords F - H bond is more stable than H - H. Good, but how does this compare to the reported bond energies of HF and H2?. Sf3014 (talk) 13:09, 22 May 2019 (BST)
The approximate position of the transition state is r1 (F - HA) = 1.8107525 Å, r2 (HB - HC) = 0.744878758 Å.
The activation energy for the reaction H + HF → F + H2 is approximately: 134.025 - 103.752 = 30.273 kcal mol-1 = 126.662 kJ mol-1
The activation energy for the reaction F + H2 → H + HF is approximately: 104.019 - 103.752 = 0.267 kcal mol-1 = 1.117 kJ mol-1 Well done, but how did you get the positions of your transition state? Also, What are these numbers that you used to calculate your activation energies? More description needed. Sf3014 (talk) 13:09, 22 May 2019 (BST)
Reaction dynamics
One set of initial conditions that has a reactive trajectory is:
| F- H distance | H - H distance | F - H momentum | H - H momentum | Etot |
|---|---|---|---|---|
| 2 | 0.74 | -0.9 | -0.6 | -103.544 |
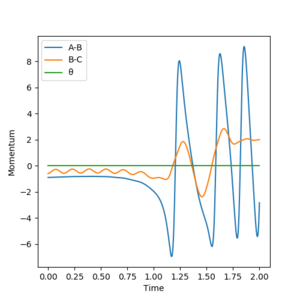

Initially, there is very low vibrational energy and the system is high in potential energy. As the reaction proceeds, it can be seen that there is an increase in the magnitude of momentum and increase in average kinetic energy while the total energy of the system remains constant. This shows itself as an increase in vibrational energy that shows itself in the HF molecule, which manifest itself as heat in the system. Being an exothermic reaction, the system releases heat to its surroundings that can be quantified as an increase in temperature. A calorimeter would be useful in quantifiying the energy released. Well done but try and be more clear next time, ie low vibrational energy of what? Also, refer to your graphs. Sf3014 (talk) 13:14, 22 May 2019 (BST)
For the reaction F + H2 → H + HF with initial conditions rHH = 0.74, rFH = 2 and momentum pFH = -0.5, a range of trajectories were calculated for a range of pHH from -3 to 3.
The step size used was 0.002.
F - HA - HB
| pHH | Etot (kcal mol-1) | Reaction? | Description |
|---|---|---|---|
| -3.0 | -96.159 | N | HA collides with F then rebounds back to HB, leaving as H2 |
| -2.9 | -96.699 | N | HA bounces between F and HB 4 times before leaving as H2 |
| -2.8 | -97.219 | N | HA bounces between F and HB 2 times before leaving as H2 |
| -2.7 | -97.719 | Y | HA bounces between F and HB 2 times before leaving as H2 |
| -2.6 | -98.199 | N | HA bounces between F and HB before immediately leaving as H2 |
| -2.5 | -98.659 | N | HA collides with F then rebounds back to HB, leaving as H2 |
| -2.0 | -100.659 | Y | HA pulled towards F as H2 moves towards F, collides and rebounds from F. Briefly stays between F and HB before getting pulled back towards F and leaves as HF |
| -1.5 | -102.159 | Y | HA bounces between F and HB 3 times before leaving as HF |
| -1.0 | -103.159 | Y | HA bounces between F and HB 2 times before leaving as HF |
| 0 | -103.659 | Y | HA bounces between F and HB 3 times before leaving as HF |
| 1.0 | -102.159 | N | HA bounces between F and HB 2 times before leaving as H2 |
| 1.5 | -100.659 | Y | HA pulled towards F as H2 moves towards F, collides and rebounds from F. Briefly stays between F and HB before getting pulled back towards F and leaves as HF |
| 2.0 | -98.659 | N | HA collides with F then rebounds back to HB, leaving as H2 |
| 2.5 | -96.159 | N | HA collides with F then rebounds back to HB, leaving as H2 |
| 2.6 | -95.599 | N | HA collides with F then rebounds back to HB, leaving as H2 |
| 2.7 | -95.019 | N | HA bounces between F and HB 3 times before leaving as H2 |
| 2.8 | -94.419 | Y | HA bounces between F and HB 9 times before leaving as HF |
| 2.9 | -93.799 | Y | HA bounces between F and HB 2 times before leaving as HF |
| 3.0 | -93.159 | N | HA collides with F then rebounds back to HB, leaving as H2 |
When momentum pFH was increased to -0.8 but pHH decreased to 0.1, the total energy of the system is very low at -103.364 kcal mol-1. This resulted in a successful reaction.
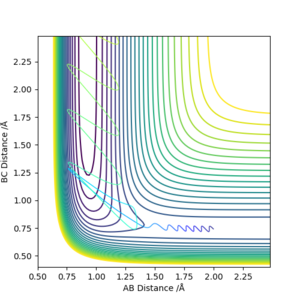
For the reverse reaction H + HF → F + H2, the initial conditions of:
| F- H distance | H - H distance | F - H momentum | H - H momentum | Etot |
|---|---|---|---|---|
| 0.92 | 2 | -17 | -18 | 36.403 |
was experimented. This gives the system a initial KE of 170.105 kcal mol-1, far above the activation energy of 30.273 kcal mol-1 for this reaction, almost 6 times the activation energy. The majority of the KE resides with the single H atom, with little to no vibration on the HF molecule. The reaction is ultimately successful and H2 is formed.

Howevery as soon as the initial KE was slightly decreased to 142.987 kcal mol-1, with initial conditions:
| F- H distance | H - H distance | F - H momentum | H - H momentum | Etot |
|---|---|---|---|---|
| 0.92 | 2 | -16 | -16.5 | 9.284 |
The reaction trajectory was unsucessful, even though the initial KE is far above the activation energy.
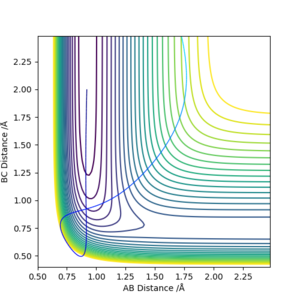
By trial and error, a set of initial conditions gives a successful reaction with only 42.492 kcal mol-1 of KE, significantly lower than previous simulations and being only about 12 kcal mol-1 higher than the activation energy. :
| F- H distance | H - H distance | F - H momentum | H - H momentum | Etot |
|---|---|---|---|---|
| 0.92 | 2 | -11.8485 | -4 | -91.208 |
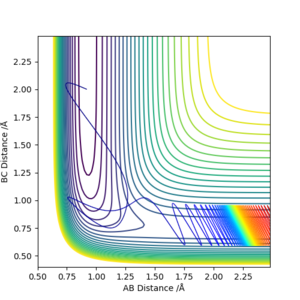
For the exothermic reaction F + H2 → H + HF, testing a wide range of values show that having high vibrational energy and high KE does not always gurantee a successful reaction, while decreasing the vibrational energy significantly and leaving it a tiny amount of KE actually resulted in a successful reaction. While for the endothermic reaction H + HF → F + H2, relying on KE alone with 0 vibrational energy shows that the system must have at least 6 times the amount of activation energy in KE (170.105 kcal mol-1) to have a successful reaction. Compared to when vibrational energy is added, only 42.492 kcal mol-1 of KE is required.
Hammond's postulate states that the transition state of a reaction most resembles the reactants or products that are closest to it in energy. In theory, this means that in an exothermic reaction, the transition state will resemble the reactants, and in an endothermic reaction, the transition state will resemble the product.
From the simulation, it appears that kinetic energy is more efficient than vibrational energy in exothermic reactions, where the transition state resembles the reactants. Where as vibrational energy is more efficient than kinetic energy in endothermic reactions where the transition state resembles the product. Indeed the Polanyi's empirical rules supports this conclusion. Well done, but there is no clear statement on Polanyi's rules, you should never assume that it's known. References for Hammond's postulate and Polanyi's rules would be good. Sf3014 (talk) 13:23, 22 May 2019 (BST)