MRD:bs517-201905

Units and indexing

Throughout this document all energies are expressed in kcal mol^-1, distances in Å, time is an arbitrary parametrisation of the trajectory. For each system with atoms A, B and C, r₁=r_AB, r₂=r_BC, p₁=p_AB and p₂=p_BC.

Exercise 1: H + H₂ system

Transition states

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

• Maximum of the minimum energy path between the reactants and products
• Saddle point on the potential energy surface; $\text{2D: }\mathrm{\nabla }i:\frac{\partial V_i}{\partial p_i}=0,D=[V_{xx}{V}_{yy}-{\left(V_{xy}\right)}^2]<0$.
• Can be located by running simulations starting from initial conditions close to, but not equal to it; these simulations either (for a sufficiently small change in initial conditions) oscillate around the transition state, or more likely, end up on the reactant/product side. A tiny change in initial conditions might change the outcome of the "reaction" completely. Simulations with the exact transition state as initial conditions will stay at the transition state indefinitely (though this cannot be achieved in practice).
• Distinguishing from local minima: simulations starting from sufficiently close to a local minimum will always stay there, oscillating; $\text{2D: }\mathrm{\nabla }i:\frac{\partial V_i}{\partial p_i}=0,D=[V_{xx}{V}_{yy}-{\left(V_{xy}\right)}^2]>0,V_{xx}>0$.

This equation looks just copied from somewhere and is not explained, please define the variables. Also it takes the gradient of the potential energy surface with respect to momentum? This doesn't really make sence. A discussion of orthogonal directions having either positive or negative second derivatives of potential energy with respect to interatomic distance would be more appropriate. Pu12 (talk) 12:59, 24 May 2019 (BST)

Locating the transition state

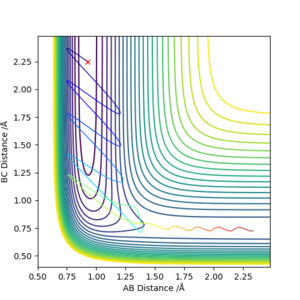
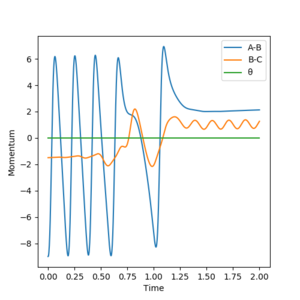
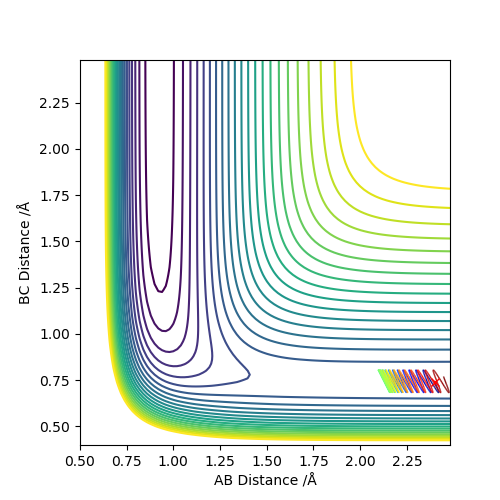
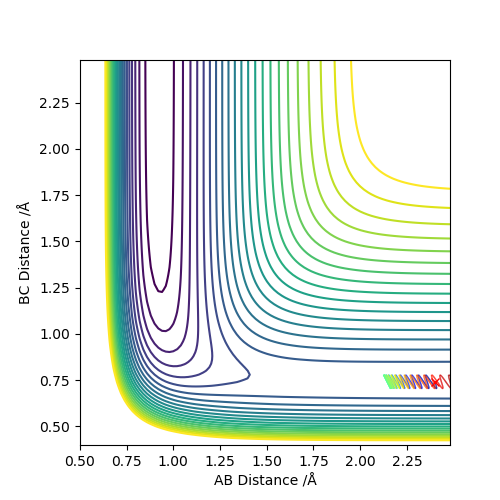
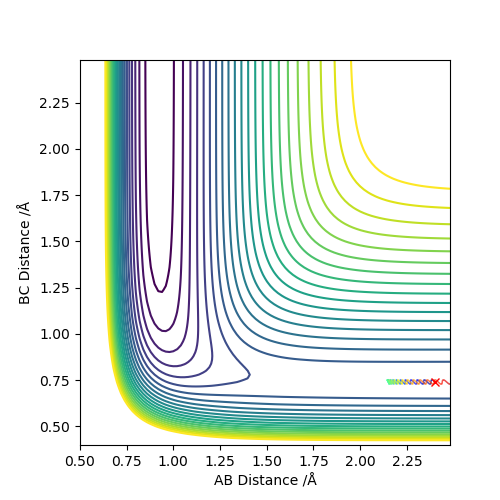
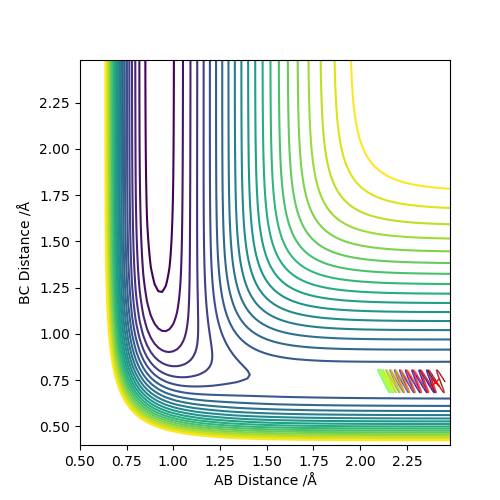
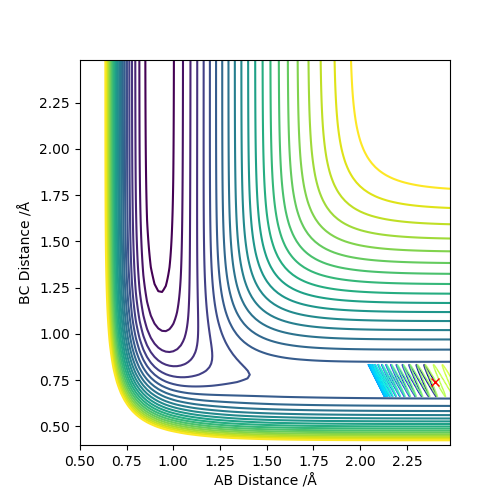
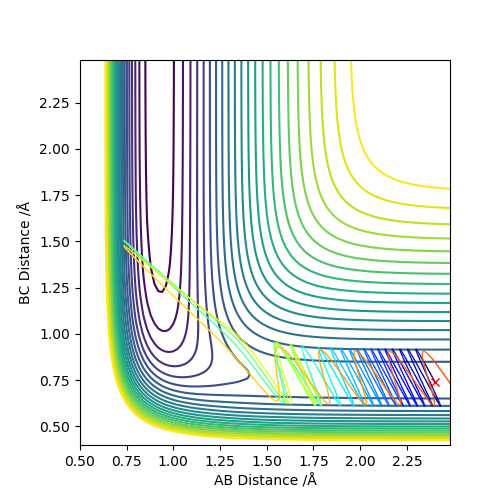
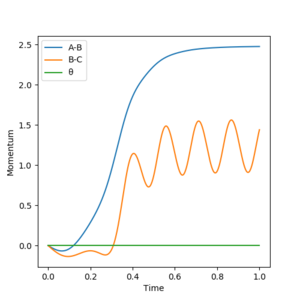
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

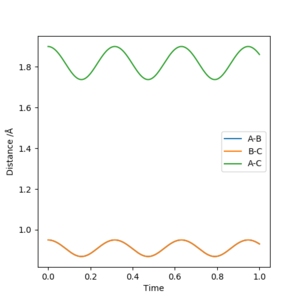
The transition state was approximated by simulations with initial conditions r₁=r₂=cst., p₁=p₂=0. For initial conditions with internuclear distances sufficiently close to that of the transition state, the atoms stay in the simulation area and an oscillatory behaviour of the atoms was observed. Contrary to the oscillations observed in simulations leading to reactions, these happen in one dimension, i.e. they go thru the transition state as their equilibrium point in every period.

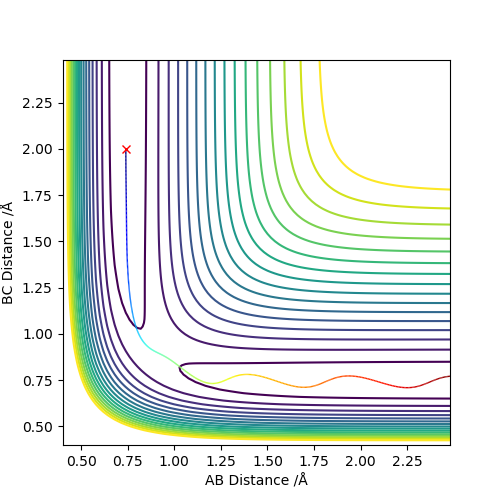
The final approximation of the transition state was reached by changing the initial conditions r₁=r₂=cst., so the amplitude of the vibrations observed in the "Internuclear Distances vs Time" plot approached zero. The smallest amplitude was observed at r₁=r₂=0.9077425=r_ts (Figure 1-3).

Figure 1: Internuclear Distances vs Time graph of H+H₂ from r₁=r₂=0.95, p₁=p₂=0. The stoms oscillate at a low amplitude, so we are close to the transition state, but not exactly on it.

Figure 2: Internuclear Distances vs Time graph of H+H₂ from r₁=r₂=0.9077≈r_ts, p₁=p₂=0. Almost no oscillation can be observed on the simulation, we almost exactly on the transition state.

Figure 3: Internuclear Distances vs Time graph of H+H₂ from r₁=r₂=0.9077=r_ts p₁=p₂=0. Vibrations can still be seen, even this close to the transition state, however, only at very high zoom.

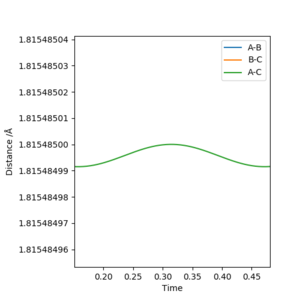
Good use of graphs. Pu12 (talk) 16:03, 23 May 2019 (BST)

Minimum energy path

Figure 4: Contour plot of the mep simulation with initial conditions r₁=r_ts+0.01, r₂=r_ts, p₁=p₂=0.

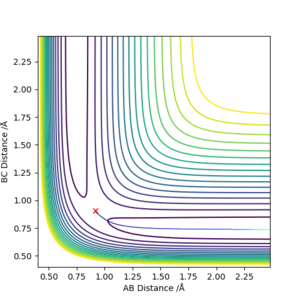
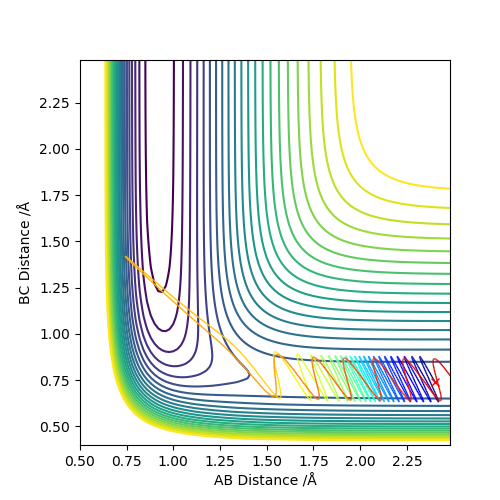
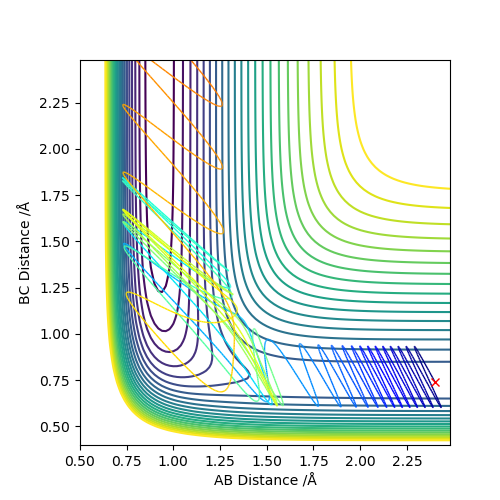
Comment on how the mep and the trajectory you just calculated differ.

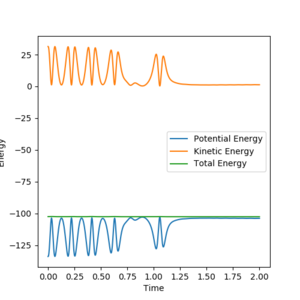
As we can see, the trajectories in Figures 4 and 5 differ in their vibrational states. As mep simulations reset the momentum of each particle to zero after every step, the particles will always move in the direction of the fastest potential energy descent around them, i.e. $\mathrm{\nabla }s\in \text{steps}:p_s\parallel -\mathrm{\nabla }V$. However, when running a Dynamics simulation the momenta are not reset, so the particles will not travel in the direction of the fastest descent, they will only be accelerated in its direction.Good. Pu12 (talk) 16:03, 23 May 2019 (BST)

This retention of their velocities causes them to overshoot the bottom of the well every time, forcing them to vibrate while moving along the surface.

Figure 5: Contour plot of the Dynamics simulation with initial conditions r₁=r_ts+0.01, r₂=r_ts, p₁=p₂=0.

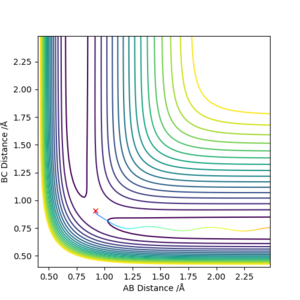
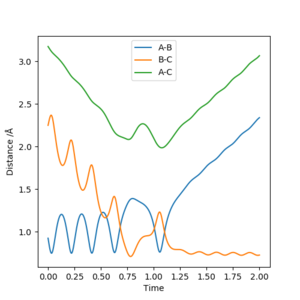
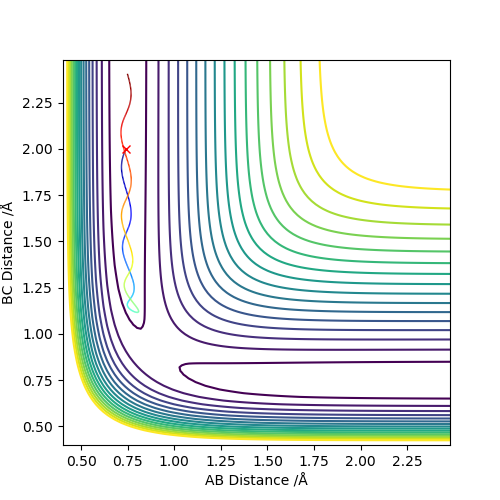
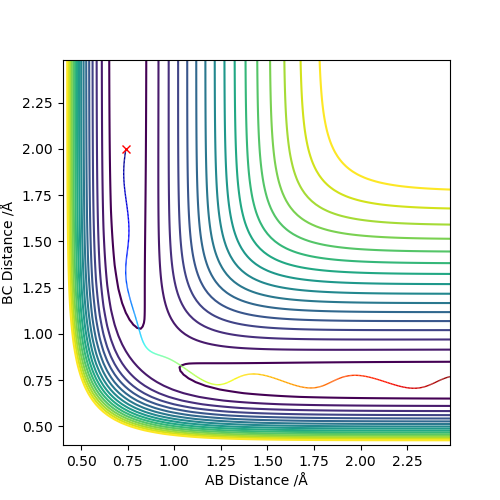
As we can see from Figures 6 and 7, B and C get closer together and farther apart from A as the reaction progresses. Running the simulation from the final positions of the above trajectory and the final momenta reversed gives us back our original initial conditions at the end of the simulation (if the simulation is done for the same number of frames with the same step size). This supports the theory that when only conservative forces are present all processes could run forwards or backwards in time as well.

Offsetting r₂ from the transition state instead of r₁ gives similar results, the only difference being that the reaction goes in the other direction towards the reactants.

Figure 6: Internuclear Distances vs Time plot of the Dynamics simulation with initial conditions r₁=r_ts+0.01, r₂=r_ts, p₁=p₂=0.

Figure 7: Momenta vs Time plot of the Dynamics simulation with initial conditions r₁=r_ts+0.01, r₂=r_ts, p₁=p₂=0.

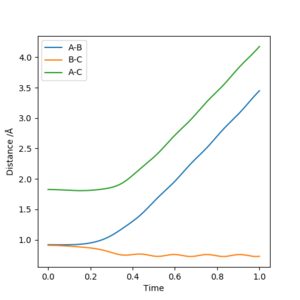
Reactive and unreactive trajectories

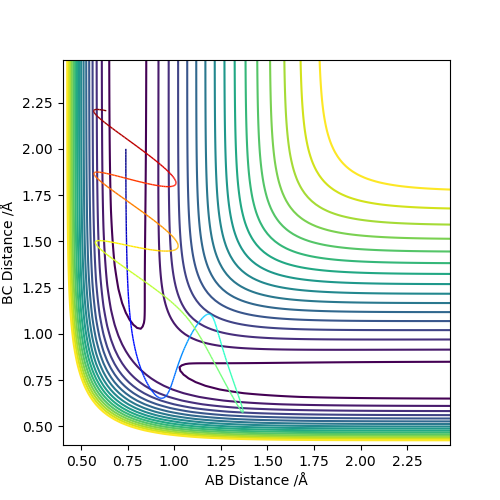
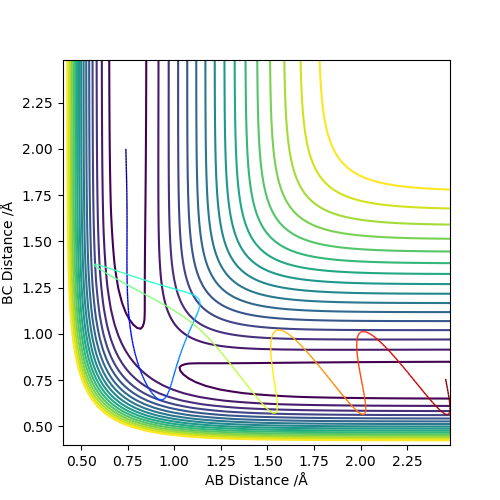
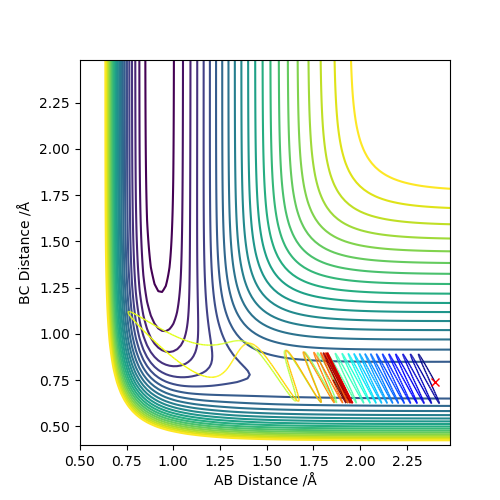
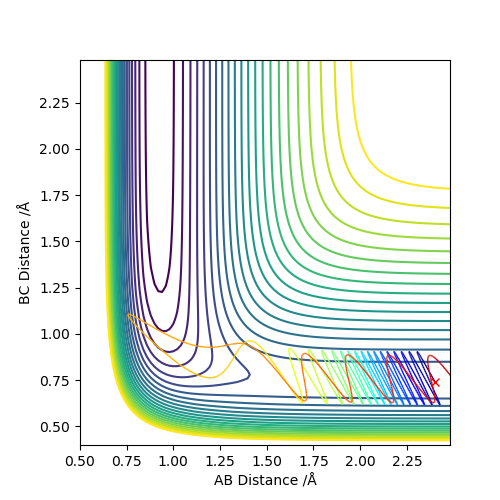
Complete the table below by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

p1	p2	Etot	Reactive?	Description of the dynamics	Trajectory
-1.25	-2.5	-99.018	Yes	Weak B-C oscillations after bond has formed
-1.5	-2.0	-100.456	No	Reaction does not reach TS
-1.5	-2.5	-98.956	Yes	Weak B-C oscillations after bond has formed
-2.5	-5.0	-84.956	No	B "bounces" voilently between A and C until finally settling with A again
-2.5	-5.2	-83.416	Yes	B "bounces" between A and C, but settles on C

You should discuss the relative motions of the atoms more in the above descriptions and refer to the crossing of the transition state more. Pu12 (talk) 16:03, 23 May 2019 (BST)

As we can see from the above table, the distribution of energies is extremely important when determining whether a reaction is going to be successful or not. In the second to last case for example the system enters the product region at a point, but it "bounces back", ultimately ending up as the starting materials again.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The assumptions of Transition State Theory are as follows:

• Born-Oppenheimer approximation
• quantum tunnelling effects are ignored
• Boltzmann distribution of energies in the reactants
• If transition state is reached with a velocity towards product state, system will not come back towards the starting materials

Experimental values are very close to those predicted by TST if all assumptions hold true. TST overestimates reaction rates if, for example, barrier recrossing is significant, and underestimates them if quantum tunnelling pathways are involved in the forwards direction. Good. Pu12 (talk) 16:03, 23 May 2019 (BST)

Exercise 2: F-H-H system

PES inspection

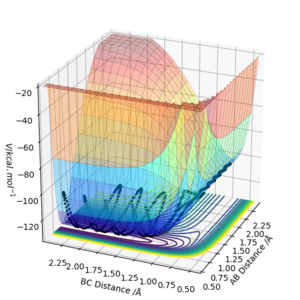
By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Locate the approximate position of the transition state.

The reaction between F + H₂ is exothermic and the reverse reaction is endothermic. We can see this from the potential energy surface, as the equipotential lines go lower on the side of the HF species. This is due to the strong H-F bond, that has a high ionic contribution, especially compared to the non-polar H-H bond.

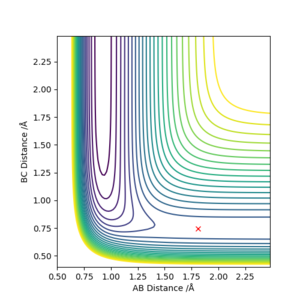
The approximate transition state is r₁=1.81069389, r₂=0.7449985 (Figure 8, 9). This was found by doing Dynamics simulations with p₁=p₂=0, and changing r₁ and r₂ towards the F + H₂ side bit by bit if the reaction went to the HF + H state, and vice versa.

Figure 8: Internuclear Distances vs Time plot of the F-H-H system from the initial conditions r₁=1.81069389, r₂=0.7449985

Figure 9: Contour plot of the F-H-H system from the initial conditions r₁=1.81069389, r₂=0.7449985

Report the activation energy for both reactions.

Transition state energy: -103.752

HF + H energy: -133.910

H₂ + F energy: -103.973

E_A(F+H₂->HF+H)=0.221

E_A(HF+H->H₂+F)=30.158

Correct. Pu12 (talk) 16:03, 23 May 2019 (BST)

Reaction dynamics

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

As we can see from Figure 10, the H-F bond at the end of the reaction vibrates much more, than the H-H bond did at the start of the reaction. This means that throughout the reaction potential energy is converted into heat energy, e.i. the vibration of the atoms. This could be confirmed by for example a simple calorimetry experiment in a bomb calorimeter.

Also translational energy is converted into vibrational. Pu12 (talk) 16:03, 23 May 2019 (BST)

Figure 10: Controur plot of the F+ H₂ system from the initial conditions r₁=2.424212428049714, r₂=0.7399019047604279, p₁=-1, p₂=-0.4

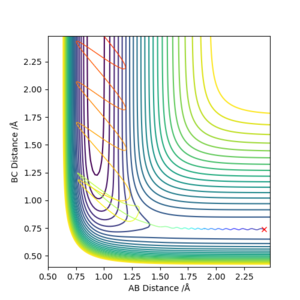
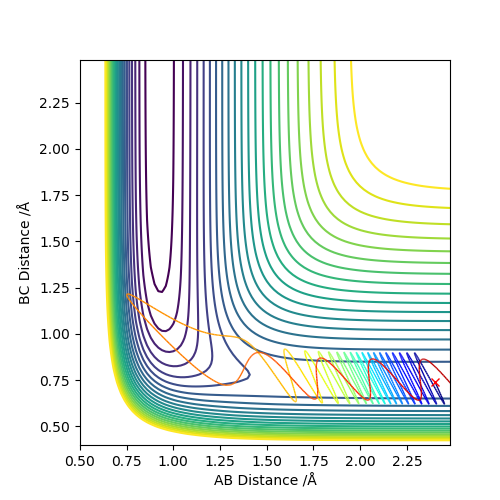
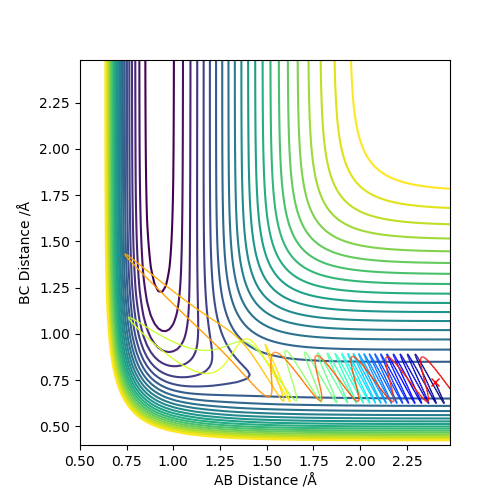
Setup a calculation starting on the side of the reactants of F + H₂, at the bottom of the well r_HH = 0.74, r_FH = 2.4, with a momentum p_FH = -0.5, and explore several values of p_HH in the range -3 to 3 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.

p1	p2	Etot	Reactive?	Description of the dynamics	Trajectory
-0.5	-3	-96.279	No	Barrier recrossing
-0.5	-2.8	-96.816	No	Barrier recrossing and re-recrossing
-0.5	-2.8	-97.339	Yes	Barrier recrossing and re-recrossing
-0.5	-2.6	-98.319	No	Barrier recrossing
-0.5	-2.4	99.219	Yes	Barrier recrossing and re-recrossing
-0.5	-2.2	-100.039	No	Does not reach TS
-0.5	-2.0	-100.779	No	Does not reach TS
-0.5	-1.5	-102.279	No	Does not reach TS
-0.5	-1	-103.379	No	Does not reach TS
-0.5	0	-103.779	No	Does not reach TS
-0.5	1	-102.279	No	Does not reach TS
-0.5	1.5	-100.779	No	Does not reach TS
-0.5	2	-98.779	No	Barrier recrossing
-0.5	2.2	-97.839	No	Barrier recrossing
-0.5	2.4	-98.819	No	Barrier recrossing
-0.5	2.6	-95.719	No	Barrier recrossing
-0.5	2.8	-94.539	No	Multiple barrier recrossings and re-recrossings
-0.5	2.9	-93.919	No	Barrier recrossing
-0.5	3	-93.279	Yes	Multiple barrier recrossings and re-recrossings
-0.8	0.1	-103.484	Yes	Only one barrier crossing, reaction is successful even though the overall energy is much lower, than in any of the other cases with a successful reaction --> better energy distribution

We can see from the table that the initial energy distribution is even more important for this reaction, than for the reactoin between H and H₂. Also, just putting more energy into the system may or may not yield a successful reaction.

Sometimes changing the initial conditions bit a tiny amount changes the outcome of the reaction completely, so though everything here is deterministic, there is an element of chaos theory involved.

The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's empirical rules are based on Hammond's postulate. They state that for endothermic reactions vibrational energy is preferred to translational energy on the reactant side, and the other way around for exothermic reactions. This is because to get up to the top of an endothermic barrier, a system with low vibrational excitation and high translational energy will not be able to pass the potential wall as it just "bounces off", usually a high vibational excitation is required to get up while going back and forth between the two walls. In the exothermic case the system is required to have high translational energy to, instead of just bouncing between the walls and going back to the reactant side, actually pass the barrier and descend to the potential well.

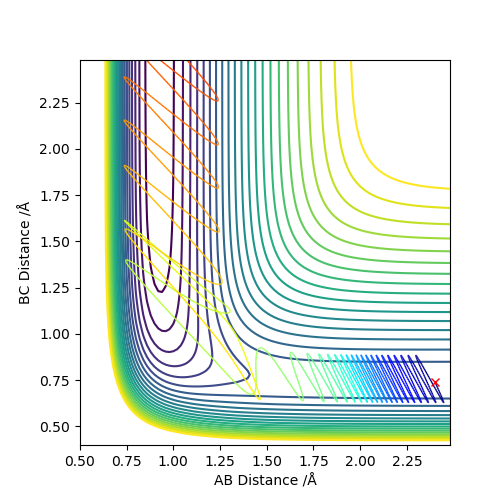
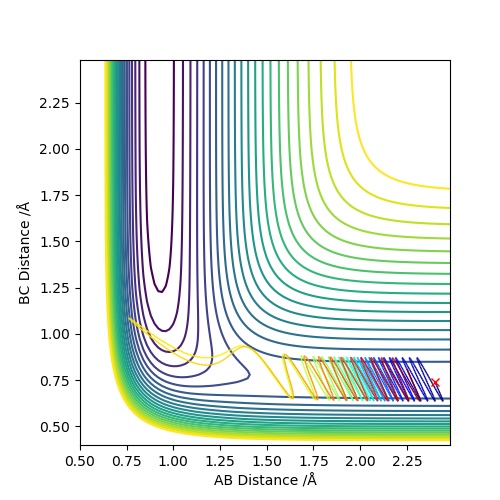
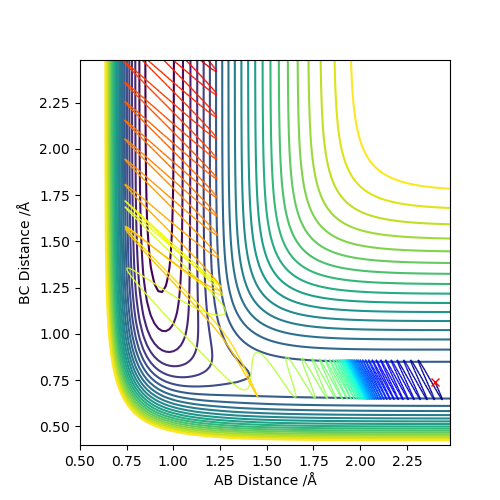
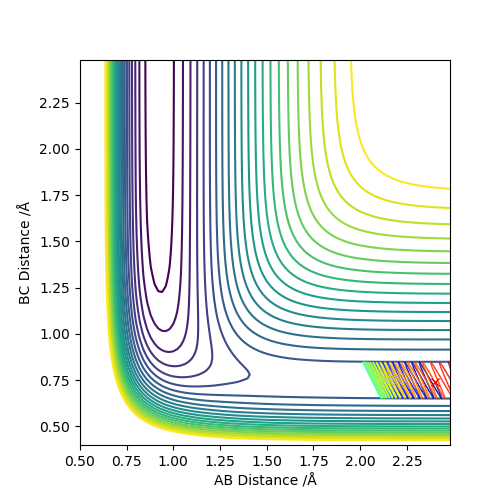
As we can see from Figures 11-15, for a reaction of HF + F with high initial viabrational energy and low initial translational energy (most of the energy of the reaction is stored in the vibrations of the F-H bond initially), the reaction succeeds even though the total energy of the system is very low (-102.463), meaning that this must be a very efficient trajectory. At first, the system bounces between the walls of the potential well (F-H bond vibrates). Next, the HF hydrogen gets passed back and forth between the F and other H atoms, finally settling with the other H atom. We can see on Figure 13, the H molecule also vibrates at the end of the reaction, but it does so significantly less violently, than the HF molecule did.

Good report overall 5/5. Pu12 (talk) 12:59, 24 May 2019 (BST)

Figure 11: Contour plot of the reaction of F + H₂ initial conditions r₁=0.925, r₂=2.25, p₁=-9, p₂=-1.5.

Figure 12: Surface plot of the reaction of F + H₂ initial conditions r₁=0.925, r₂=2.25, p₁=-9, p₂=-1.5.

Figure 13: Internuclear distances vs Time plot of the reaction of F + H₂ initial conditions r₁=0.925, r₂=2.25, p₁=-9, p₂=-1.5.

Figure 14: Energies vs Time plot of the reaction of F + H₂ initial conditions r₁=0.925, r₂=2.25, p₁=-9, p₂=-1.5.

Figure 15: Momenta vs Time plot of the reaction of F + H₂ initial conditions r₁=0.925, r₂=2.25, p₁=-9, p₂=-1.5.