MRD:bl2518
Overall great job on this report. You have answered each section correctly with a good discussion. To improve I would recommend referencing throughout.
Exercise 1
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is a set of configurations through which successful reactive trajectories must pass. It is a saddle point on PES. At the saddle point, the slope of the function is set to zero (i.e. V'(r1)=V'(r2)=0). Although, the saddle point and minimum has the same slope of the function (i.e. slope=0), they can be distinguished by the second derivatives, curvatures, of the function. A saddle point is characterized by a negative curvature in one direction and positive curvature in the other directions. The second derivatives of a minimum are positive in both directions. [1]
Good. You could include the point regarding the TS being a maximum on a minimum energy pathway... What do the second derivative positive and negative values signify in terms of a maximum and minimum? Mys18 (talk) 19:58, 21 June 2020 (BST)
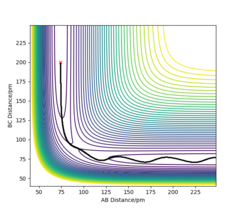
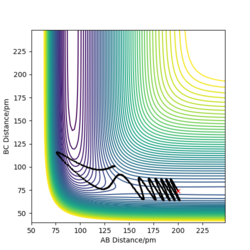
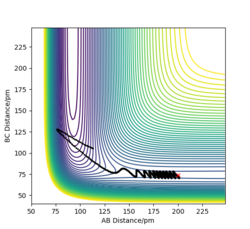
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
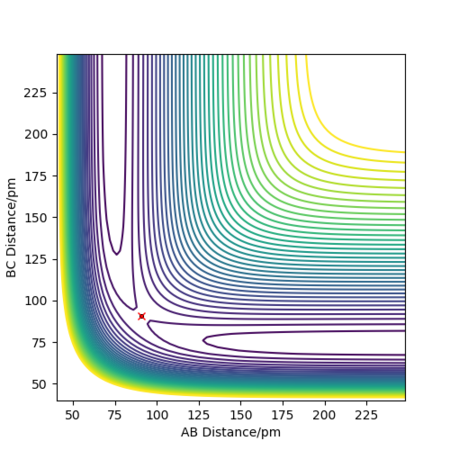
rts = 90.8 pm
If we start the trajectory at the transition state, it will remain stationary there forever. This means that in the "Internuclear Distances vs Time” plot, functions should be straight lines. Also, forces along AB and BC are almost 0 N. Also, from the contour plot, only a dot is shown which represents a transition state.
Good. Mys18 (talk) 20:00, 21 June 2020 (BST)
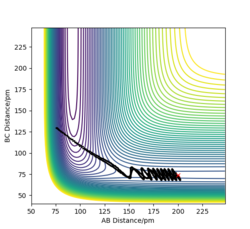
Comment on how the mep and the trajectory you just calculated differ.
| Dynamics | MEP | |
|---|---|---|
| contour plot |  |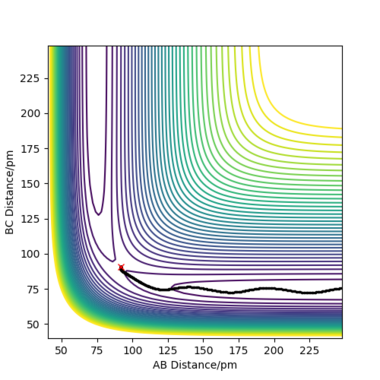
|
| "Internuclear Distances vs Time” plot |  |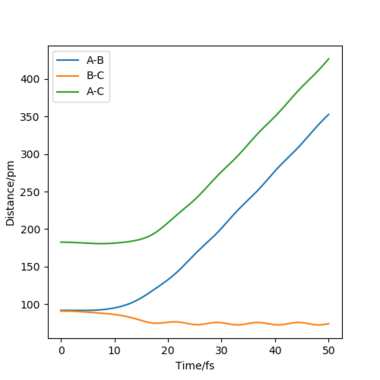
|
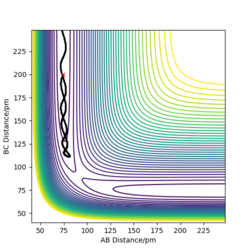
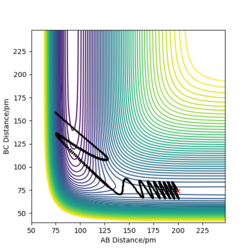
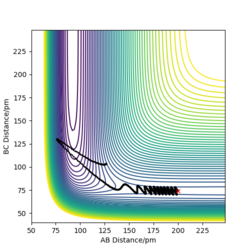
To compare these two calculation types, rAB and rBC are set to be 91.8 pm and 90.8 pm, respectively. However, the momentums are both set to be 0 g.mol-1.pm.fs-1. As for dynamics and MEP calculations, HA are moving away from HB-HC. The main difference is that dynamics calculation shows internal vibration of HB-HC bond as rBC is fluctuating, which is shown by two plots in the table above. However, MEP calculation does not take account of the HB-HC bond vibration, the BC distance is unchanged when AB distance increase. HA and HB-HC just follow the floor of the valley. Also, from the "Momenta vs Time" plot, momenta are zero since as for each time step the momentum is set to be zero.
| Dynamics | MEP | |
|---|---|---|
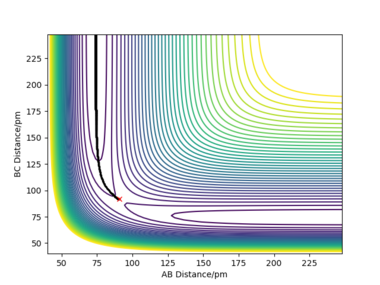
| contour plot |  |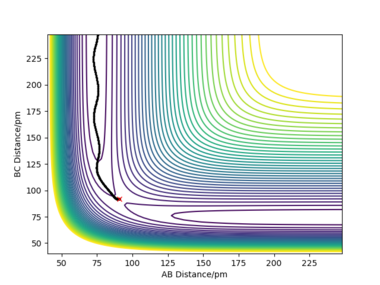
|
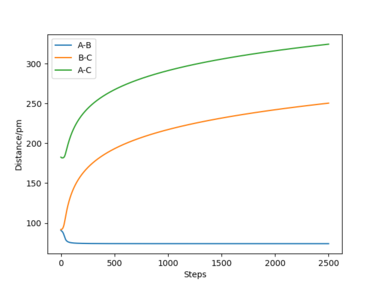
| "Internuclear Distances vs Time” plot |  |
|
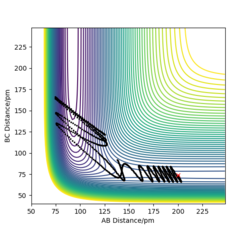
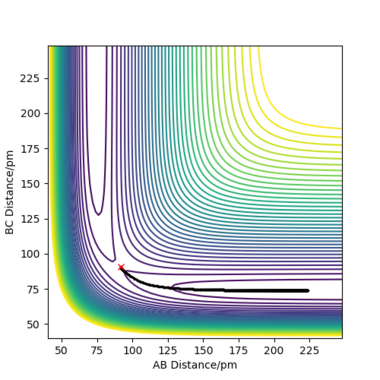
When rAB and rBC are set to be 90.8 pm and 91.8 pm, respectively, the final product become HA-HB and HC. To clarify, at this time, the transition state geometry is changed in the direction HA-HB by very small amount (i.e. AB distance is smaller). Thus, it rolls towards HA-HB rather than HB-HC. However, MEP still does not take account atomic motions and the momenta are zero.
Well done. Hence we see a more 'wavy' plot for Dynamic. Which do you think is more realistic, MEP or Dynamic?)
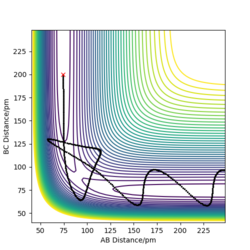
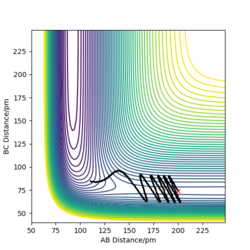
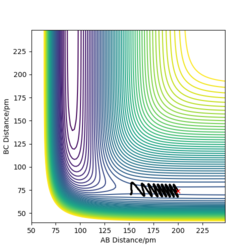
When I set up a calculation where the initial positions correspond to the final positions of the trajectory, the same final momenta values but with their signs reversed. HA-HB collides the HC and form HB-H and HA. As a result, we have a reactive reaction that has sufficient energy to overcome the transition state.
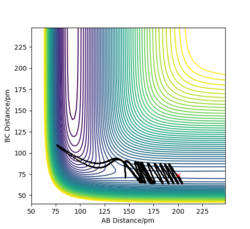
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.280 | Yes | The AB distance is small but BC distance is large. However, momenta provided are sufficient to pass the transition state. As a result, HC substitues HA to form HB-HC. Also, HA is moving away from the molecule so AB distance increases contantly. (KE=19.508 kJmol-1) | 
|
| -3.1 | -4.1 | -420.077 | No | The diatomic molecule has a largrer momentum, so it has a stronger vibration mode.The BC has a smaller momentum. Although the total energy is larger, the reaction is not reactive. The total energy includes potential energy and kinetic energy. In this case, it has larger potential energy but smaller kinetic energy than the previous case. Thus, it does not have enough energy to pass the transition state. (KE= 13.710 kJmol-1) | 
|
| -3.1 | -5.1 | -413.977 | Yes | The molecule has the same momentum as the second one, but the BC momentum is larger. Therefore, they have higher kinetic energy and have the sufficient energy to pass the transition state to form HB-HC. At the same time, atom A moves away. (KE= 19.810 kJmol-1) | 
|
| -5.1 | -10.1 | -357.277 | No | In this case, the energy (kinetic energy is much larger than previous cases) is too high to form HB-HC. Firstly, atom C approaches HA-HB. C collides HA-HB, HA-HB bond is broken. Then, HB-HC is formed. However, this system is too energetic, so HB-HC vibrates vigorously. As a result, the bond is broken again and HA-HB is formed. (KE= 76.510 kJmol-1) | 
|
| -5.1 | -10.6 | -349.477 | Yes | In this case, they have enough energy to reach the transition state. HA-HB bond is broken quickly, and form HB-HC. Because of very high energy, BC bond is broken and form HA-HB. However, the kinetic energy is slightly higher than the previous one. As a result, AB bond is broken again and form a BC molecule. Finally, BC molecule is stable, but still has relatively large vibration. The trajectory moves in the direction of the product. (KE= 84.310 kJmol-1) | 
|
The hypothesis which states "It would seem fair to assume that all trajectories starting with the same positions but with higher values of momenta (higher kinetic energy) would be reactive, as they have enough kinetic energy to overcome the activation barrier." is not completely correct. By increasing the kinetic energy (momentum), it is more likely to have a reactive reaction. When AB momentum in unchanged, by increasing BC momentum the reaction becomes reactive. However, a reactive reaction is not guaranteed by a high kinetic energy. To explain, the 4 th case has higher energy than previous cases but it is not a reactive reaction.
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Overall, the Transition State Theory overestimates the rate constant.
The theory assumes that once the energy of the system is higher than the energy of the transition state, the reaction is reactive. However, this is not true. As shown in the table above, the 4 th case has enough energy, but the reaction is not reactive since the product could recross the energy barrier to reform the reactant. Although, in reality the possibility is low. Thus, the theory overestimates the rate constant.
Possibility of recrossing is not low in the assumption, but it says the reaction goes to completion.
Apart from this, the Transition State Theory is based on classical mechanics. All of quantum mechanics effects (e.g. tunelling) are ignored. Even if the energy of the reaction is not enough to overcome the energy barrier, the reaction could happen via tunelling. Hence, this underestimate the rate constant, but this is a minor effect.
Good it should still be considered even if less significant for heavier atoms. Some references you could add to your assumptions, also a few more assumptions of TST.
Exercise 2
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
Nice job on your discussion. Reference for your experimental values?
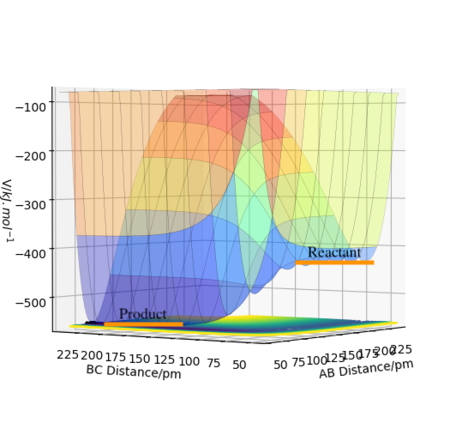
In F-H-H system, AB distance and BC distance are F-H distance and H-H distance, respectively.
By inspection the PES, the F + H2 reaction is exothermic, as the product has lower energy. However, the H + HF reaction is endothermic. The products of the F + H2 reaction is just the reactants of the H + HF reaction, so the enthalpy change values of the reactions should be the same but in the opposite sign.
Experimental bond energies of H-H and H-F are 432 kJ/mol and 565 kJ/mol, respectively. The bond energy of the H-F is larger since H-F bond is polar and has partial ionic character. As for the F + H2 reaction, the energy is needed to break a H-H bond. Then, the H-F bond formation releases energy. The energy released is larger than the energy required to break a bond so the reaction is exothermic. Inversely, as for the H + HF reaction, the energy released from the H-H formation is smaller so the reaction is endothermic.
Locate the approximate position of the transition state. Report the activation energy for both reactions.
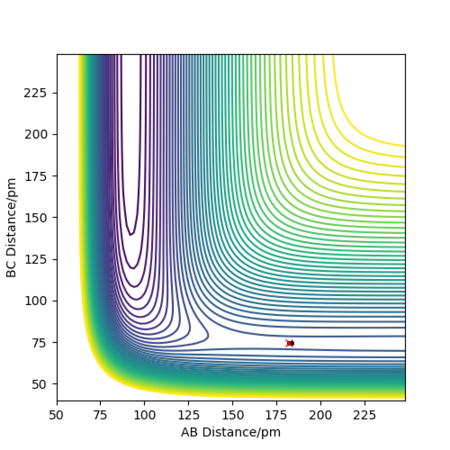
The transition state for F-H-H system is that rAB = 182.3 pm and rBC = 74.50 pm. Its energy is -433. 981 kJ/mol.
If we start the trajectory at the transition state, it will remain stationary there forever. This means that in the "Internuclear Distances vs Time” plot, functions should be straight lines. Also, only a dot in the contour plot.
Report the activation energy for both reactions.
By using MEP and setting rAB = 1000 pm and rBC = 74 pm to obtain:
the potential energy of F + H2 is -435.057 kJ/mol so the activation energy for them = -433. 981 - (-435.057) = 1.076 kJ/mol
By using MEP and setting rAB = 91 pm and rBC = 1000 pm to obtain:
The potential energy of H + HF is -560.404 kJ/mol so the activation energy = -433.981 - (-560.404) = 126.423 kJ/mol
Values look as expected :).
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
rHF = 200 pm and rHH = 74 pm
| pHF/ g.mol-1.pm.fs-1 | pHH/ g.mol-1.pm.fs-1 | Reactivity? | Illustration of the trajectory |
|---|---|---|---|
| -1.0 | 6.1 | No | 
|
| -1.0 | 5.1 | No | 
|
| -1.0 | 4.1 | Yes | 
|
| -1.0 | 3.1 | Yes | 
|
| -1.0 | 2.1 | No | 
|
| -1.0 | 1.1 | Yes | 
|
| -1.0 | -2.1 | Yes | 
|
| -1.0 | -3.1 | No | 
|
| -1.0 | -4.1 | Yes | 
|
| -1.0 | -5.1 | No | 
|
| -1.0 | -6.1 | No | 
|
By running 11 simulations, it can be concluded that the reactivity of the reaction does not depend on the energy put. If the energy is too high, it has possibility to reform the reactants; if the energy is too low, it may not be enough to pass the transition state. When the momenta increases, the vibration becomes more and more vigorous. Therefore, the energy could be released as vibrational energy. In addition, particles move faster when the momenta is increased so the energy is released as translational energy.
This can be confirmed by infrared chemiluminescence (IRCL) which can measure the intensities of photons emitted from vibrationally excited molecules. The intensities can be used to assess the population of vibrational states of molecules. The HF has a lot vibrational energy so the higher vibrational energy states could be populated. Thus, overtones should be generated in the spectrum. After the relaxation, the state populated mostly is the ground state, so in the spectrum, the intensity of the peak is higher while the intensities of their overtones should be lower.
Great explanation! You could even use what you know from your answer above regarding the overall reaction being exo.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Great explanation showing understanding of Polanyi's rule with referencing!
The Polanyi rules state that the vibrational energy is more efficient in promoting a late-barrier reaction than the translational energy, but is less efficient in promoting a early-barrier reaction than the translational energy. [2]
As for H + HF endothermic reaction, it has a late transition state that resembles the product. The H-F bond must be stretched. It is true that energy is needed to push the molecule up to the transition state, but without bond stretching we cannot access the transition state. As a result, vibrational efficiency is very high to access the transition state. As shown in the figures below, when vibrational momentum PHF is high, the reaction is reactive even if the translational momentum PH-H is low. However, in the second figure, the translational momentum PH-H is higher, and kinetic energy is also higher. The reaction is unreactive.
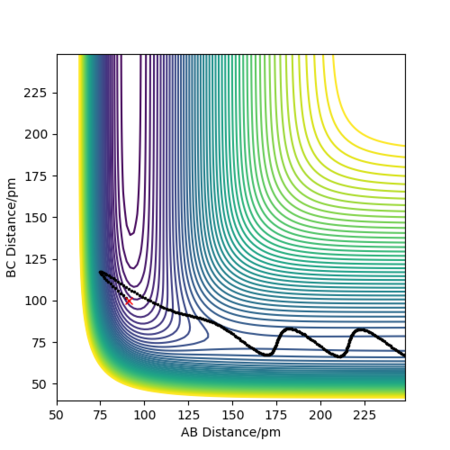
As for F+ H2 exothermic reaction, it has an early transition state that resembles the reactant. There is no need to change the structure of the reactants, so the vibration stretching is not important. If we have the sufficient translational energy to push the molecule up the hill to the transition state, the reaction will be reactive. As shown in the figures below, when translational momentum is larger the reaction is reactive. However, when the vibrational momentum and total energy are larger, the reaction is not reactive. Hence, the translational energy is more efficient in promoting a early-barrier reaction.
