Atom-Diatom Collisions

OVERALL COMMENTS: A good report overall, although you made a major error calculating the transition state energies. 4/5

Exercise 1: H+H₂ System

Dynamics from the transition state region

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

A potential energy surface diagram maps the potential energy of the total system relative to physical parameters such as r₁ and r₂. The transition state occurs at a saddle point on the potential energy surface ie. where ∂V(r₁)/∂r₁= 0 and ∂V(r₂)/∂r₂= 0; ∂²V(r₁)/∂r₁²< 0, ∂²V(r₂)/∂r₂²> 0 or vice versa (one of the second derivatives will be negative). The constraints on the second partial derivatives with respect to r₁ and r₂ differentiate the saddle point from the local minimums of the surface which correspond to the reactants and products, for which ∂²V(r₁)/∂r₁²> 0, ∂²V(r₂)/∂r₂²> 0. As both first partial derivatives are equal to 0, the system is stable exactly at the transition state (but unstable with a minute perturbation to either side of the transition state). This means the transition state can be identified as a system which has no kinetic energy.

Good answer. One thing that you haven't done though is defined r1 and r2, are these the rAB/rBC vectors in the programs PES? If not, a diagram of the PES showing the basis vectors of r1 and r2 would be helpful.

Report your best estimate of the transition state position (r_ts) and explain your reasoning, illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

If the system is set up in the geometry of the transition state with no initial momentum, then it should remain in the transition state geometry indefinitely and have no kinetic energy. Furthermore, in the symmetrical H_a+ H_bH_c-> H_aH_b+ H_c system, the distances between the atoms, r₁ and r₂, must be equal in the transition state, i.e. r₁=r₂ (this constraint may also prevent the transition state from being confused with the minima associated with reactants/products, where r₁>r₂ and r₂>r_1).

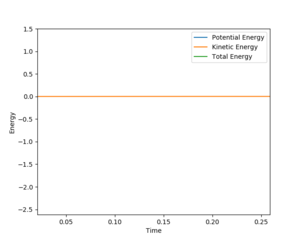
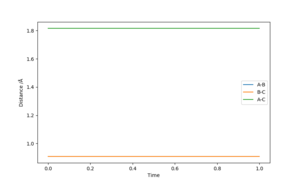
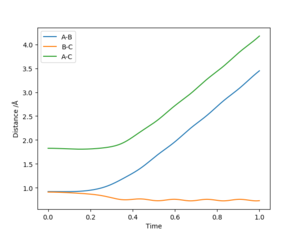
Energy vs time graphs were plotted by repeatedly inputting increasingly accurate values for r₁ and r₂ (with r₁=r₂) into Leps Gui, with p₁= p₂= 0 (as there is no kinetic energy there is no momenta), with the values for r₁ and r2 improved via trial and improvement until a plot was obtained where the kinetic energy was static at 0 J as seen in figure 1. The internuclear-distance vs time graph was plotted for these r₁/r₂/p₁/p₂ values, and showed r₁ and r₂ to be static and equal at r_ts= r₁= r₂= 0.9077432 Å, i.e. the atoms are stationary as the system is in the transition state, as seen in figure 2.

Figure 1: Energy vs time graph showing no kinetic energy being present in the transition state, where r₁= r₂= r_ts= 0.9077432 Å and p₁= p₂= 0.

Figure 2: Internuclear-distance vs time graph for the transition state of the reaction H_a+ H_bH_c -> H_aH_b + H_c,showing constant and equal values for r₁ and r₂ at 0.9077432 Å.

Comment on how the MEP and the trajectory you just calculated differ.

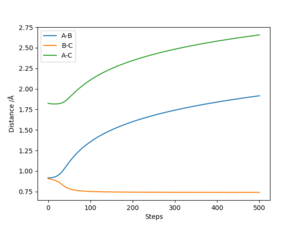
The MEP, figure 3 and 4, and the dynamic trajectory, figure 5, were both plotted with r₁ = r_ts+ 0.01 = 0.9177432 Å, r₂ = r_ts= 0.9077432 Å and p₁ = p₂ = 0. The MEP predicts that under these circumstances the internuclear distances r₁ and r₂ will both tend to constant values (ie. the atom H_a will move increasingly slowly away from H_b/H_c), while the internuclear distance r₂ (really the H_b-H_c bond length) will settle relatively quickly to a constant value (with no vibration). The predictions of H_a's motion becoming infinitely slow, and the absence of vibration in the H_b-H_c bond (i.e. a constant r₂ after the collision) is due to the MEP ignoring the inertial motion of atoms.

Good answer! I'd say that you've reported the value of rTS to an excessive number of decimal places (to an accuracy of about 1/50th the width of a single proton)

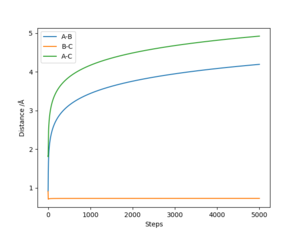
Figure 3: Internuclear-distance MEP plotted with 500 steps of size 0.002, for initial conditions r₁ = r_ts+ 0.01 = 0.9177432, r₂ = r_ts= 0.9077432 and p₁ = p₂ = 0.

Figure 4: Bond-distance MEP plotted with 5000 steps of size 0.01 for initial conditions of r₁ = r_ts+ 0.01 = 0.9177432, r₂ = r_ts= 0.9077432 and p₁ = p₂ = 0.

Meanwhile, the dynamic model shows the r₁ and r₁+r₂ internuclear distances increasing by a positive gradient which has some slight sinusoidal variation, i.e. H_a moves away from H_bH_c at a constant velocity, but the internuclear distances do not increase with a constant gradient because of the H_b-H_c vibration. This H_b-H_c vibration is also seen in the r₂ bond length, which varies sinusoidally around a constant value of ~ 0.74 Å. The momenta vs time plot for these initial conditions gives values of p₁= 2.5, and p₂= 1.25 after 1 second.

Figure 5: Dynamic bond-distance vs time plot where initially r₁ = r_ts+ 0.01 = 0.9177432, r₂ = r_ts= 0.9077432 and p₁ = p₂ = 0.

What would change if we used the initial conditions r₁ = r_ts and r₂ = r_ts+ 0.01 instead?

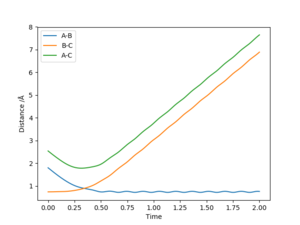
When the initial conditions are reversed, so that r₁ = r_ts+0.01 = 0.9077432 Å, r₂ = r_ts= 0.9177432 Å, p₁ = p₂ = 0; both the internuclear-distance vs time and momenta vs time plots for r₁ exactly resembles that for r₂ under the initial conditions, and the plot for r₂ exactly resembles that for r₁ under the initial conditions. This is because exactly the same sort of collision is occurring, but with H_a colliding with the diatomic H_bH_c to form a new diatomic H_aH_b which H_c moves away from, instead of H_ccolliding with H_bH_aforming a new diatomic H_cH_b which H_a moves away from as occurred under the initial conditions of r₁ = r_ts+ 0.01 = 0.9177432 Å, r₂ = r_ts= 0.9077432 Å, p₁ = p₂ = 0. The H_a+ H_bH_c-> H_aH_b+ H_creaction is symmetrical, so when the forwards reaction occurs instead of the reverse then all the plots stay the same and just the atom assignments change.

Set-up a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?

The internuclear distance vs time plot shown in figure 6 was created with the conditions r₁ = 0.8 Å, r₂= 0.74 Å, p₁= -2.5, and p₂= -1.25. It shows A approach the diatomic B-C (which is not vibrating), pass through a transition state where r₁ = r₂ at the intersection of the lines, then A and B remain in a new diatomic which vibrates sinusoidally, with bond length r₁ varying around 0.74 Å, while C travels away with a constant velocity. A reaction therefore occurs under these conditions.

Figure 6: A bond-distance vs time plot with the initial conditions r₁ = 0.8, r₂= 0.74, p₁= -2.5, and p₂= -1.25.

Reactive and un-reactive trajectories

Complete the table by adding the total energy, whether the trajectory is reactive or un-reactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

p₁	p₂	E_tot(3 d.p.)	Reactive?	Description of the dynamics	Figure
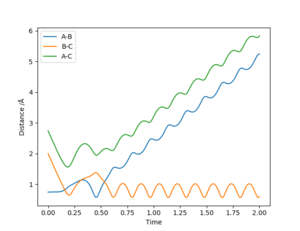
-1.25	-2.5	-99.018	Yes	C approaches AB, A leaves BC (small vibration).	7
-1.5	-2.0	-100.456	No	C approaches AB, C repelled by AB (small vibration) before any significant interaction occurs.	8
-1.5	-2.5	-98.956	Yes	C approaches AB, A leaves BC (small vibration).	9
-2.5	-5.0	-84.944	No	C approaches AB, large distortion occurs with a barrier recrossing so that C is expelled by the TS and leaves AB (large vibration).	10
-2.5	-5.2	-83.390	Yes	C approaches AB, large distortion occurs and A leaves BC (large vibration).	11

We can conclude that the hypothesis stands - i.e. all trajectories for initial conditions r₁ = 0.74 Å, r₂ = 2.0 Å, -1.5 < p₁ < -0.8, and p₂ = -2.5 are reactive. Meanwhile, trajectories were tested with p₂ values other than -2.5, and some were reactive and some were un-reactive (and this did not seem to correspond to having larger or smaller p₂values than -2.5). Furthermore, whether the reaction occurs or not appears to be independent of p₁, although there are larger vibrations in the diatomic products for reactions occurring with higher p₁ values (and greater distortion in the transition states).

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory states that, with sufficient (activation) energy, colliding atoms/molecules will form a high energy unstable complex known as a transition state, which can decay back into the original reactants or go on to form new products. The transition state is assumed to exist in a dynamic equilibrium with the reactants, so that the conversion of reactants to products can be re-written as a two-step process of reactants (with sufficient activation energy) forming a transition state and then this transition state subsequently decaying to form products. The transition state will take on the vibrational/rotational/electronic/translational energy of the reactants, eg. the linear triatomic A..B..C produced from the collision of C and AB (with sufficient energy) will have stretching and bending vibrational modes, however Transition State Theory does not implement selection rules for the transfer of these quantised energies. Furthermore, Transition State Theory assumes atoms/molecules follow classical mechanics, particularly in the requirement of the products to have a minimum activation energy in order to form a transition state upon their collision - which is disputed by the quantum tunnelling of small particles described by quantum mechanics.

Transition State Theory would predict that all reactant collisions with sufficient energy would lead to a reaction occurring. This does not agree with the barrier crossing in our results, as seen in figure 10, where the system crosses the transition state region but goes on to reform the products anyhow (perhaps due to a quantum mechanical restriction from a selection rule not being met?). Transition State Theory therefore has limitations despite its use in modelling elementary chemical reactions, and the prediction that the rate of a reaction will increase if the activation energy is more readily available (i.e. through higher temperatures) may be disputed by experiment.

Good answer and most things are correct, although I think you could make your answer slightly clearer in a few ways: (1) would predict that all reactant collisions with sufficient energy would lead to a reaction occurring - more specifically, any system that reaches the TS goes on to form products (2) perhaps due to a quantum mechanical restriction from a selection rule not being met I doubt this, it is more likely that the first product formed has so much energy that it is unstable (and so dissociates); after the first recrossing, the energy of the system is distributed in such a way that the resulting products are far more stable. (3) prediction that the rate of a reaction will increase if the activation energy is more readily available (i.e. through higher temperatures) - Given your results, this is reasonable, do you expect to see multiple recrossings at low temperatures then (hint: yes you should)? If so then what can you say about the accuracy of TS theory over all conditions?

Exercise 2: F - H - H system

PES inspection

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F + H₂: exothermic - because the polar covalent F-H bond formed is much stronger than the purely covalent H-H bond broken (the large electronegativity difference between F and H causes an electrostatic attraction which reinforces the covalent bond between the two atoms) so more energy is released than absorbed.

H + HF: endothermic - because the energy released by the formation of the weaker H-H bond is not sufficient to compensate for the energy absorbed in the breaking of the strong F-H bond, so energy is absorbed from the environment to make up the difference.

Locate the approximate position of the transition state.

At the transition state, all the atoms will be instantaneously stationary, so there will be no kinetic energy in the system and the total energy will be equal to the potential energy. Hammond's Postulate states that the transition state will most resemble in structure the reactants or products which it is closest in energy to. As the transition state for the reaction F + H₂ -> H + HF is closest in energy to the high energy reactants (as the reaction is exothermic), the transition state structure will be most similar to F + H₂, with r₁ (the F-H internuclear-distance) being longer than the average F-H bond length of 0.92 Å by a greater extent than r₂ (the H-H internuclear-distance) is longer than the average H-H bond length of 0.74 Å.

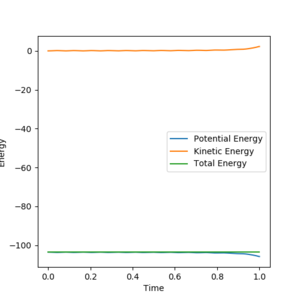
Through trial and improvement to find the energy vs time plot with kinetic energy nearest to zero, the internuclear-distances in the transition state were found to be r₁= r_ts1 = ~1.70 Å and r₂= r_ts2 = ~0.77 Å, while the momenta are of course p₁ = p₂ = 0. The energy vs time plot for these initial conditions (which should remain constant!) is shown in figure 12, where it is possible to see the slightly sinusoidal kinetic and potential energy curves (due to the diatomic vibrating), which also deviate from their average values after a significant period of time.

Figure 12: Energy vs time graph used in approximating the internuclear distances in the transition state for F + H₂ -> H + HF as r₁= ~ 1.70 Å, r₂= ~ 0.77 Å, with momenta p₁ = p₂ = 0.

Report the activation energy for both reactions

An MEP, as shown in figure 13, was run with the initial conditions r₁= r_ts1 + 0.01 = 1.70 + 0.01 = 1.71 Å, r₂= r_ts2 = 0.77 Å, p₁ = p₂ = 0; and with 1000 steps of size 0.01. The energy MEP gave a constant total energy for the transition state of -133.9870. It was certain the transition state had been reached as the kinetic energy was constant at 0.

An energy vs time MEP was used to find the reactants' total energy (ie. for F + H₂ with r₁=3, r₂ =0.74, p₁=p₂=0) as -103.9903. Therefore, the activation energy for F + H₂ -> FH + H is -133.9870 - (-103.9903) = -29.9967.

An energy vs time MEP was used to find the products' total energy (ie for FH + H with r₁ = 0.92, r₂=3, p₁=p₂=0) as -133.9974. Therefore, the activation energy for FH + H -> F + H₂ is -133.9870 - (-133.9974) = 0.0104. As it is unlikely that the transition state is lower in energy than the products, this very small positive value is likely due to the limits of the precision of the program.

These calculations are incorrect. What is the physical meaning of a negative activation energy? Also, using your chemical intuition, does it make sense that the magnitude of the activation energy for F+H2 is higher than FH+H?

Figure 13: An internuclear-distance MEP with initial conditions r₁= 1.71 Å, r₂= 0.77 Å, p₁ = p₂ = 0; from 1000 steps of size 0.01.

Reaction dynamics

Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

A reactive trajectory for F + H_bH_c -> FH_b + H_cis achieved for the initial conditions r₁ = 2, r₂ = 0.74, p₁ = -1.25, and p₂= -1.5, as shown by the internuclear-distance vs time plot seen in figure 14, with r₁= the F-H_b internuclear-distance and r₂=the H_b-H_c internuclear-distance. The animation and momenta vs time graph show far greater bond vibrations in the HF diatomic product than in the H₂ reactant, due to the energy 'released' by the exothermic reaction (from the higher potential energy of the reactants) being converted to the kinetic energy of the products (so the total energy in the system remains constant). The conversion of potential energy to kinetic energy (i.e. vibrational, rotational and translational motion) could be measured as an increase in temperature during the course of a reaction. An increase in the diatomic vibrational energy could be measured through Raman or IR spectroscopy, and the decrease in potential energy from reactants to products can be seen in the products having a lower dissociation energy than the reactants.

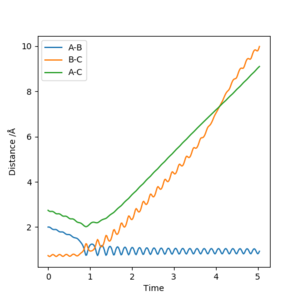
Figure 14: Internuclear distance vs time graph for initial conditions r₁ = 2, r₂ = 0.74, p₁ = -1.25, and p₂= -1.5.

Setup a calculation starting on the side of the reactants of F + H₂, at the bottom of the well r_HH = 0.74, with a momentum p_FH= -0.5, and explore several values of p_HH in the range -3 to 3 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.

Internuclear-distance vs time graphs were plotted for r₁= 2 Å, r₂= 0.74 Å, p₁= -0.5, and -3 > p₂ < 3, in order to discover if a reaction of F + H_bH_c -> FH_b + H_c would occur when the system was given these initial conditions. The activation energy required to reach the transition state was exceeded in every system, so all of the interactions reached transition states, and many then lead to the formation of products. However, the transition states reached in some systems collapsed to reform the product, eg. for p₂ = -2.9, -1.5, 1, 2.2, involving barrier recrossing (which may be due to selection rule restrictions). Furthermore some systems, eg. with p₂ = 0.4, 1.1, continually returned to the transition state from repeat barrier recrossing, so that the three atoms remain in a triatomic system in a constant state of flux. The reaction took place at the range limit of p₂ = 3.000, however not at p₂ = -3.000 (although it did for p₂ = -2.998), and also took place when p₂ = 0 (after several barrier crossings and re-crossings). Whether a reaction occurs (or not) does not appear to be linked to the size (or sign) of p₂. The values of p₂ which prevent the transition state from forming products due to barrier recrossing(s) appear to be fairly random (and perhaps due to restrictions from selection rules).

When a reaction does occur, the vibrational energy of the diatomic product HF is seen to be much greater than the vibrational energy of the diatomic reactant H₂. As seen from the animation (and internuclear-distance vs time graphs) the HF bond vibration is caused by the movement of the (light) H_b atom - hence the F-H_c bond length does not show such large vibrations as the H_b-H_c bond length. The size of the diatomic product's vibrations do not appear to be proportional to the initial momentum of the H₂ diatomic bond p₂ - for example, they appear to be roughly the same size for p₂= 0 as for p₂= 2.9 as for p₂= -2.8.

For example, figure 16 shows the trajectory for a system with initial conditions r₁= 2 Å, r₂= 0.74 Å, p₁= -0.5, and p₂= 0.1, which is reactive.

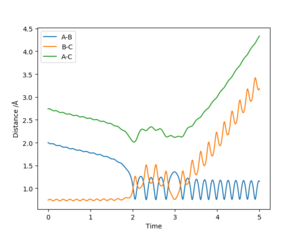
Figure 16: Internuclear-distance vs time plot for initial conditions r₁= 2, r₂= 0.74, p₁= -0.5, p₂= 0.1.

For the same initial position, increase slightly the momentum p_FH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum p_HH = 0.1. What do you observe now?

When the system is given the initial conditions r₁= 2 Å, r₂= 0.74 Å, p₁= -0.8, and p₂= 0.1, the reaction takes place following a brief barrier crossing, as shown in figure 17. The higher p₁ value increases the speed at which the H atom leaves the diatomic HF product in comparison to under the previous initial conditions (seen in figure 16). There are also less barrier crossings in the formation of the products, which makes the rate of reaction around twice as fast as with the previous conditions.

Figure 17: Internuclear-distance vs time graph for a system with initial conditions r₁= 2, r₂= 0.74, p₁= -0.8, and p₂= 0.1.

Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H-F bond, and an arbitrarily high value of p_HH above the activation energy (an H atom colliding with a high kinetic energy).

We now consider the reaction H_a + H_bF -> H_aH_b + F, where r₁is the H_a-H_b internuclear-distance and r₂is the H_b-F internuclear-distance. Figure 18 gives the internuclear-distance vs time plot with initial conditions r₁= 5 Å, r₂= 0.92 Å, p₁= -10, and p₂= -0.01, and shows an un-reactive trajectory due to a barrier crossing.

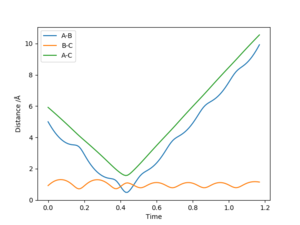
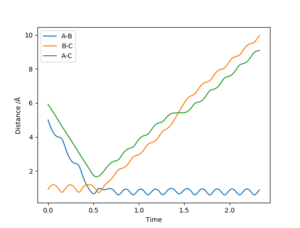
Figure 18: The internuclear-distance vs time plot with initial conditions r₁= 5, r₂= 0.92, p₁= -10, and p₂= -0.01.

Try to obtain a reactive trajectory by decreasing the momentum of the incoming H atom and increasing the energy of the H-F vibration.

Figure 19 shows the internuclear-distance vs time plot from initial conditions r₁= 5 Å, r₂= 0.92 Å, p₁= -8, and p₂= -0.1, giving a reactive trajectory.

Figure 19: The internuclear-distance vs time plot with initial conditions r₁= 5, r₂= 0.92, p₁= -8, and p₂= -0.1.

The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's empirical rules state that for reactions with early transition states, a large difference in the translational energies of the reactants is best in achieving the required activation energy, while for reactions with late transition states a large vibrational excitation of the reactants is best for achieving the required activation energy.

As discussed earlier, the reaction F + H₂-> HF + H is exothermic so has an early transition state, while its reverse, H + HF -> H₂ + F, is endothermic so has a late transition state. In both reactions, the value of p₁ indicates the translational speed at which the atom reactant approaches the diatomic reactant, as none of the kinetic energy indicted by this momentum value can be stored as vibrational energy (and the amounts stored by rotation are always very small in comparison). Meanwhile, the value of p₂ indicates the vibrational energy of the diatomic (through bond stretching/bending) as any translation energy the diatomic has will only act to increase/decrease the value of p₁ because only the relative translational speeds are considered.

In the reaction F + H₂-> HF + H, initial conditions with high p₁ translational energies resulted in reactions occurring, no matter the values of p₂ (apart from some disallowed values most likely due to selection rules). As this is the exothermic reaction with the early transition state, this fits with Polanyi's empirical rules.

Meanwhile, in the reaction, H + HF -> H₂ + F, initial conditions with a higher p₂ vibrational energy resulted in a previously un-reactive reaction occurring, despite a lower value of p₁. As this is the endothermic reaction with the late transition state, the fits with the latter of Polanyi's empirical rules.

Good!