MRD:at3815
EXERCISE 1: H + H2 system
Gradient of the potential energy surface at minimum and transition state
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The gradient of the potential energy surface at both the minimum and at a transition structure is zero.
At a minimum, the curvature shows a local minima of the potential energy surface. The second derivative at that point would be positive, where the gradient of the potential energy surface is negative before the minimum point, zero at the minimum point, and positive after the minimum point.
At a transition state, the curvature shows a saddle point. The second derivative at that point is also zero, where the sign of the gradient of the potential energy surface remains the same before and after that point.
(Fv611 (talk) 11:39, 24 May 2017 (BST) A bit of confusion, as the second derivative at the TS is not zero, and as the gradient around the TS point depends on the coordinate it is calculated on.)
Locating transition state
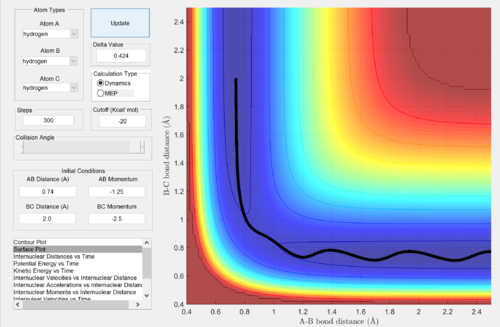
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
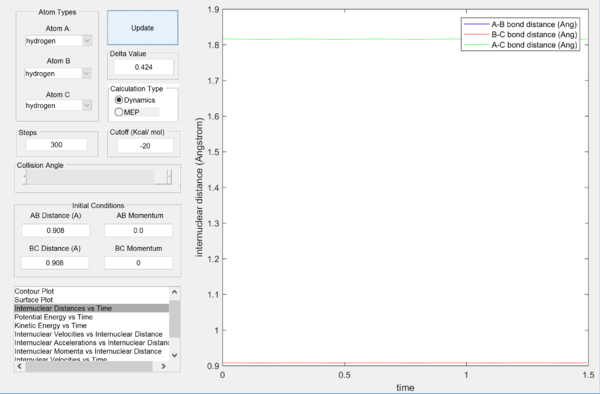
rts = 0.908 Å
The rts was obtained by determining the distance between the atoms at which the gradient of the graph of internuclear distances vs time is as close to zero as possible, depicting a horizontal straight line. This shows that the oscillations in the atoms are minimal, suggesting that the atoms are at the minimum potential energy and thus near equilibrium position. Any deviations from this distance would lead to oscillations in the graph, which shows that the atoms are moving away from its equilibrium position.
Reaction path: MEP vs Dynamics
Comment on how the mep and the trajectory you just calculated differ.
The trajectory of mep is a straight line where it follows the valley floor to the final products without oscillation, following the direction of the steepest slope at each step. However, when the calculation type is changed back to dynamics, an oscillating trajectory is obtained, where the initial velocity of the atoms is taken into account into their pathway.
(Fv611 (talk) 11:39, 24 May 2017 (BST) Good that you mentioned the velocities, but could have expanded on why taking into account velocity makes a difference. Could also have added plots of both to compare them.)
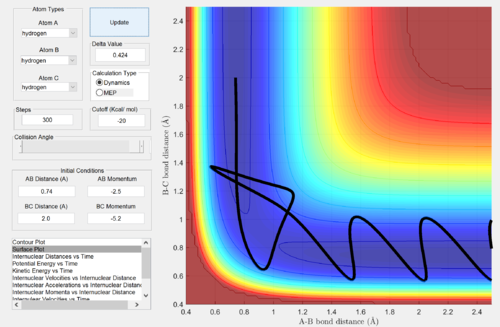
Reactive and unreactive trajectories
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Reactive/Unreactive | Trajectory | Description | |
|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | Reactive |  |
As C approaches A-B, there is sufficient momentum and kinetic energy to overcome the activation energy required to reach the transition state and the reactants collide and react to form A + B-C. A moves further away from B-C, while the B-C bond distance oscillates between 0.70 to 0.77 Å due to vibrational energy. |
| 2 | -1.5 | -2.0 | Unreactive |  |
As C approaches A-B, there is insufficient BC momentum and thus kinetic energy to overcome the activation energy to form B-C. This is shown in the surface plot where the distance of B-C decreases to about 1.1 Å, before C rebounds and move further away A-B. The bond length of A-B remains relatively constant and oscillates around 0.70 to 0.77 Å due to vibrational energy. |
| 3 | -1.5 | -2.5 | Reactive |  |
As C approaches A-B, there is sufficient momentum and kinetic energy to overcome the activation energy required to reach the transition state and the reactants collide and react to form A + B-C. A moves further away from B-C, while the B-C bond distance oscillates between 0.70 to 0.77 Å due to vibrational energy.
Due to the larger initial momentum of A-B, there is higher kinetic and vibrational energy, resulting in an oscillating trajectory at the beginning. However, the products still have more vibrational energy than the reactants. |
| 4 | -2.5 | -5.0 | Unreactive |  |
As C approaches A-B, there was sufficient kinetic energy to overcome the transition state. The products of A + B-C was temporarily formed, where the bond distance of B-C was shorter than that of A-B. However, barrier recrossing occurs and the products eventually reverts back to the reactants. C moves away from B-C and B-C is reformed with a larger amount of vibrational energy than it's initial state. |
| 5 | -2.5 | -5.2 | Reactive |  |
As C approaches A-B, there is sufficient kinetic energy to overcome the transition barrier thrice, where initially the reactants form the products of A + B-C, then barrier recrossing occurs to form back the reactants, and once again the products are formed. A then moves further away from B-C and B-C oscillates with large vibrational energy. |
Transition State Theory
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The main assumptions[1][2] of Transition State Theory are as follows:
1) The quasi-equilibrium assumption. The theory assumes that the activated complexes and the reactants are in quasi-equilibrium with each other even when equilibrium between the reactants and products are not achieved.
2) It is assumed that for each elementary step of a multi-step reaction, the lifetime of each intermediate is long enough to reach a Boltzmann distribution of energies before proceeding on to the next step.
3) It is assumed that atomic nuclei behaves according to classic mechanics; that unless atoms or molecules collide with sufficient energy to form the transition state, the reaction does not occur. Quantum tunneling is not observed.
4) The theory assumes that the reaction system will take the pathway of the lowest energy saddle point on the potential energy surface. However at high temperatures, molecules populate higher energy vibrational modes where their motion becomes more complex and collisions may lead to transition states with energy higher than that of the saddle point.
The reaction rates predicted by the Transition State Theory differs from experimental values as the above assumptions do not hold true in reality. From reaction 4 and 5 above, it can be seen that barrier recrossing occurs. This shows that the molecules merely having energy equivalent to that of the activation energy is not sufficient for a reaction to occur, whereas the theory suggests that products will be formed if the reactants have sufficient energy to form the transition state. Furthermore in reaction 4, it is observed that the reactants reformed despite having enough energy to initially overcome the activation energy. Therefore, the Transition State Theory will overestimate the rate of the reaction compared to that obtained in experimental.
(Fv611 (talk) 11:39, 24 May 2017 (BST) Good)
EXERCISE 2: F - H - H system
Potential Energy Surface
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
| Reaction | Energetic Process | |
|---|---|---|
| 1 | F + H2 --> HF + H | Exothermic |
| 2 | H + HF --> H2 + F | Endothermic |
As the first reaction is exothermic while the second is endothermic, this indicates that the formation of HF is more favoured than of H2. This suggests that the bond strength of H-F is larger than that of H-H. This is supported by literature values of bond strength[3] of H-F and H-H, where the bond energies are 570 kJ/mol and 436 kJ/mol respectively.
(Fv611 (talk) 11:39, 24 May 2017 (BST) How did you figure out these reactions are exo/endothermic? You should have related your answers to the potential energy surfaces.)
Locating Transition State
Locate the approximate position of the transition state.
The transition state is approximated to be where rHF = 1.810 Å and rHH = 0.745 Å.
Activation Energies
Report the activation energy for both reactions.
Energy of transition state = -103.8
| Reaction | Potential Energy/ kcal mol-1 | Activation Energy Ea/ kcal mol-1 |
|---|---|---|
| F + H2 --> HF + H | -103.9 | 0.1 |
| H + HF --> H2 + F | -133.9 | 30.1 |
The activation energies for the reactions of F + H2 --> HF + H and H + HF --> H2 + F are 0.1 kcal mol-1 and 30.1 kcal mol-1 respectively.
(Fv611 (talk) 11:39, 24 May 2017 (BST) Again, where are you getting these from?)
Reaction Dynamics
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
 |
 |
|---|
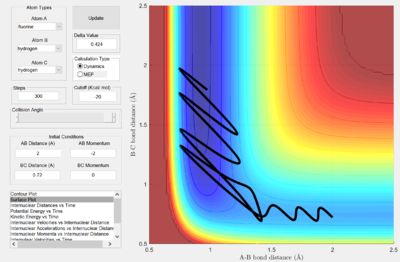From the reactive trajectory seen above, it can observed that the initial momentum from the approaching F is released as vibrational energy, where it interconverts between kinetic and potential energy. It can be seen that H-F oscillates with a large amount of vibrational energy as the graph of internuclear momentum against time shows the (blue) wave with a large amplitude after the collision occurs at approximately where time = 0.6.
The use of infrared chemiluminescence[4] can be used to observe the emission of infrared photons from the vibrationally excited product molecules after formation. If there is loss in energy through heat, this can be observed through any changes in temperature of the reaction.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The efficiency of a reaction is affected by the distribution of energy between the translational and vibration modes of the reactants. According to Polanyi Rules[5], it states that vibrational energy is more efficient in promoting a reaction with a late transition state than translational energy; while translational energy is more efficient in promoting a reaction with an early transition state. According to Hammond's postulate, the transition state of an endothermic reaction is closer in energy to the products than the reactants, and of an exothermic reaction, it is closer in energy to the reactants than to the products and hence has an early transition. Therefore it can be deduced that a higher proportion of vibrational energy is required to overcome the activation energy for an endothermic reaction (e.g H + HF --> H2 + F), whereas for an exothermic reaction (e.g F + H2 --> HF + H), a higher proportion of translational energy is required for an efficient reaction.
(Fv611 (talk) 11:39, 24 May 2017 (BST) Discussion is ok, but you should have related it to examples, to show your understanding.)
References
- ↑ H. Eyring, The Activated Complex in Chemical Reactions, J. Chem. Phys., 1935, 3 (2): 107–115. doi:10.1063/1.174960
- ↑ K. J. Laldler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664.
- ↑ Y. Luo, Bond Dissociation Energies, 2009, 65–98
- ↑ W. H. Duewer and D. W. Setser, Infrared Chemilumin. energy partitioning from React. Fluor. atoms with hydrides carbon, silicon, Oxyg. sulfur, nitrogen, phosphorus, 1973, 2310
- ↑ J. M. Bowman, Theor. Study Validity Polanyi Rules Late- Barrier Cl + CHD 3 React., 2012, 4, 4–7