MRD:asp216
EXERCISE 1: H + H2 system
Dynamics from the transition state region
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
At the initial and final minima, ∂V/∂r1=0 for each respective bond distance and ∂V/∂r2≠0. The second derivatives are both positive (minimum)
Transition state is at a saddle point potential energy surface, ∂V/∂ri=0, where the minimum energy path reaches a maximum. At this point the one second derivative is positve (minimum) and the orthoganal is negative (maximum).
Trajectories from r1 = r2: locating the transition state
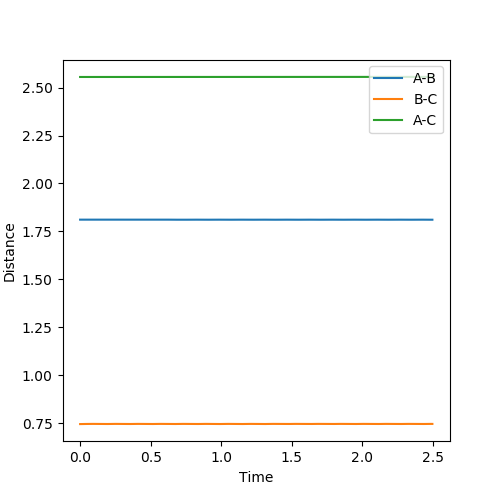
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
From the contour plot, it could be seen that the transition state is at the saddle point in the minimum energy path. For the symmetrical system, r1=r2 at the transition state. An estimate for rts=0.9 was refined by analyzing the internuclear distance/momentum vs time, so that the distance was constant (no vibration/oscillation) and momentum = 0, which are true when starting at the transition state with no initial momentum. An estimate of rts=0.90774249785 was achieved, in which internuclear distance appeared constant and internuclear momentum was of the order 10-10.
Calculating the reaction path and Trajectories from r1 = rts+δ, r2 = rts
Comment on how the mep and the trajectory you just calculated differ.
When the r1 length is slightly increased from the transition state length and all initial momenta are zero, the molecule formed is BC. When r2 length is slightly increased from the transition state length, an AB molecule is formed.
The mep just follows the surface along the minimum of the surface, with final position values r1=9.983, r2=0.756 and average momenta at T p1=0.00135, p2=0.0000654. Where as the trajectory has oscillations across the minimum due to vibrations within the molecule formed. The final position was r1=9.983, r2=0.756 and average momenta at T p1=2.48, p2=1.25.
For a trajectory calculation that takes these final position values as initial position and the momenta with opposite sign, the molecule and particle come together as and approach the transition state. However, there is insufficient energy to pass over the energy barrier for the reaction to take place and therefore the molecule is unchanged. The molecule and particle separate after the collision.
Reactive and unreactive trajectories
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
initial positions r1 = 0.74 and r2 = 2.0 Jas213 (talk) 18:23, 11 May 2018 (BST) I like that you stated the initial conditions. Would have been nice to say what you are planning to do/what method you used "dynamic" or "mep" etc.
| p1 | p2 | Total Energy | Reactive/Unreactive | Plot | Comment |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Reactive |  |
The initial conditions have sufficient energy to pass over the transition state barrier to products. AB + C --> A + BC
What does the wiggly line tell you? |
| -1.5 | -2.0 | -100.456 | Unreactive |  |
The initial conditions do not have sufficient energy to pass over the transition state barrier to products, so no reaction occurs. AB + C -X-> A + BC |
| -1.5 | -2.5 | -98.956 | Reactive |  |
The initial conditions have sufficient energy to pass over the transition state barrier to products. AB + C --> A + BC |
| -2.5 | -5.0 | -84.956 | Unreactive |   |
The initial conditions provide sufficient energy to pass over the transition state barrier and products form.
However, the product molecule has sufficient energy that its vibration causes a further collision with the atom and reacts again back to the initial reactants. AB + C --> A + BC --> AB + C |
| -2.5 | -5.2 | -83.416 | Reactive |   |
Same as above but the reformed reactants vibrate enough to collide again with sufficient energy to overcome the transition barrier again and become products. |
Jas213 (talk) 18:40, 11 May 2018 (BST) The recrossing can be very nicely seen in the Internuclear Distance vs. Time plot, which you provided in addition to the contour plot. Why did you not comment on them? Overall correct and good, but maybe try to be a bit more specific, eg. don't talk about energy in general, but about kinetic energy and potential energy. Also an overall concluding comment on what you learned from this table would have been expected underneath.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
TST assumes that at the transition state barrier (saddle point), reactants are in equilibrium with the transition state complex. This complex has a specific configurational structure, which must be crossed in order to transform into products. Hence, the rate of reaction is really the rate of collisions which form this structure.
As the theory counts each crossing the barrier as a reaction, clearly an overall unreactive recrossing (even number of crossings) and reactive recrossings (odd number of crossings) are misinterpreted. Therefore, TST predictions will be an overestimate of experimental values. At temperatures where the thermal energy is less than the transition barrier, excess energy is limited and recrossing is less likely to occur, so TST is a useful estimate. This classical approach does not account for quantum mechanical considerations such as tunneling.[1]
EXERCISE 2: F - H - H system
PES inspection
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 --> HF + H reaction is exothermic, as the products are lower in energy than the reactants (shown in the surface plot). Therefore, the reverse reaction H + HF --> H2 + F is endothermic. Hence, HF is a stronger bond than H2, as more energy is released on formation.
The bond energy of H-F is 565 kJmol-1 and the bond energy of H2 is 432 kJmol-1.
Locate the approximate position of the transition state.
Through the same method as in exercise 1, the position of the transition state is approximately r1=1.811, r2=0.744. Hammond's postulate states the more similar the energy of a transition state and the reactant/product, the more similar the structures. The activation energy of F + H2 --> HF + H is small and therefore the transition state will have a similar structure to the reactants so r2 is approximately equal to the H2 bond length. This is seen in the figure.
Jas213 (talk) 18:26, 11 May 2018 (BST) Good job mentioning how you obtained the TS. However, what does the Distance vs. Time plot show you? How do you know you found a TS?
Report the activation energy for both reactions.
By following the mep when slightly displaced either side of the transition state, energy vs time graphs will show the change in potential energy of the transition state and the products formed. This is equal to the activation energy needed to react each set of species.
For F + H2 --> HF + H the activation energy was found to be approximately 0.2 kcal/mol
For HF + H --> F + H2 the activation energy was found to be approximately 30 kcal/mol.
Reaction dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
As the atom and molecule collide, the kinetic energy is transferred into potential energy. Before the collision, the H2 molecule vibrates, shown by the oscillation in internuclear momentum. Upon collision both the internuclear momentum of H2 and H---F increases as kinetic energy is converted to potential energy. As the reaction occurs, the internuclear momentum between H2 and potential energy released (due to the exothermic nature of the reaction) is transferred to the HF formed, which vibrates at a high energy level.
Jas213 (talk) 18:33, 11 May 2018 (BST) Good that you showed the trajectories you tried, however it would be easier to follow if you explicitly stated the starting conditions and which way round you are looking at the reaction. Also none of your figures have titles or numbers, hence it is hard to know to which plot the text is referring to.
| pHH | Plot | Reactive/Unreactive |
|---|---|---|
| -3 |  |
Unreactive |
| -2.5 |  |
Unreactive |
| -2 |  |
Reactive |
| -1 |  |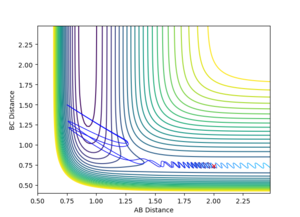
Unreactive |
| 0 |  |
Reactive |
| 1 |  |
Reactive |
| 2 |  |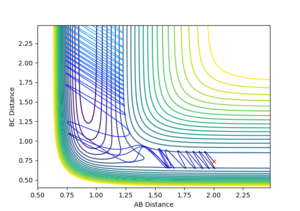
Reactive |
| 2.5 |  |
Unreactive |
| 3 |  |
Unreactive |
At the boundaries of the limit chosen (-3,3), the reaction is unreactive. When the applied momentum is relatively large compared to the activation energy (~0.2 kcal/mol), there is an excess of vibrational energy in the HH bond. The energy is transferred to H-F vibration, which is so great that there is sufficient energy to pass back over the transition barrier (~40 kcal/mol. Closer to the activation energy the reaction is reactive.
For: pFH = -0.8 and pHH = 0.1 the outcome is reactive. There is less vibrational energy in the colliding H2 molecule and when this is transferred to the fluorine atom does not have enough energy to pass back over the transition barrier and so the products remain HF + H.
For the HF + H reaction r1=0.92, r2=2.2, phf=0.5, ph=-9:
Here the H atom collides with the HF molecule with great enough kinetic energy such that transfers enough energyit can pass over the activation barrier to form products.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
For an exothermic reaction with an early transition state (F + H2), the highest impacting method of crossing the energy barrier is to have increased momentum between the the atom and the molecule colliding, through transnational (kinetic) motion.
For an endothermic reaction, with a late transition state (HF + H), the most impacting method to cross the activation energy barrier is to increase the internuclear momentum between the molecule's nuclei. This therefore increases the vibrational energy of the reacting molecule. [2]
The above contour diagrams demonstrate this principle.
Jas213 (talk) 18:37, 11 May 2018 (BST) Correct. These rules are called the Polanyi rules.